Without using the formula of equivalent. Find out charge on capacitor and current in all the branches as a function of time.
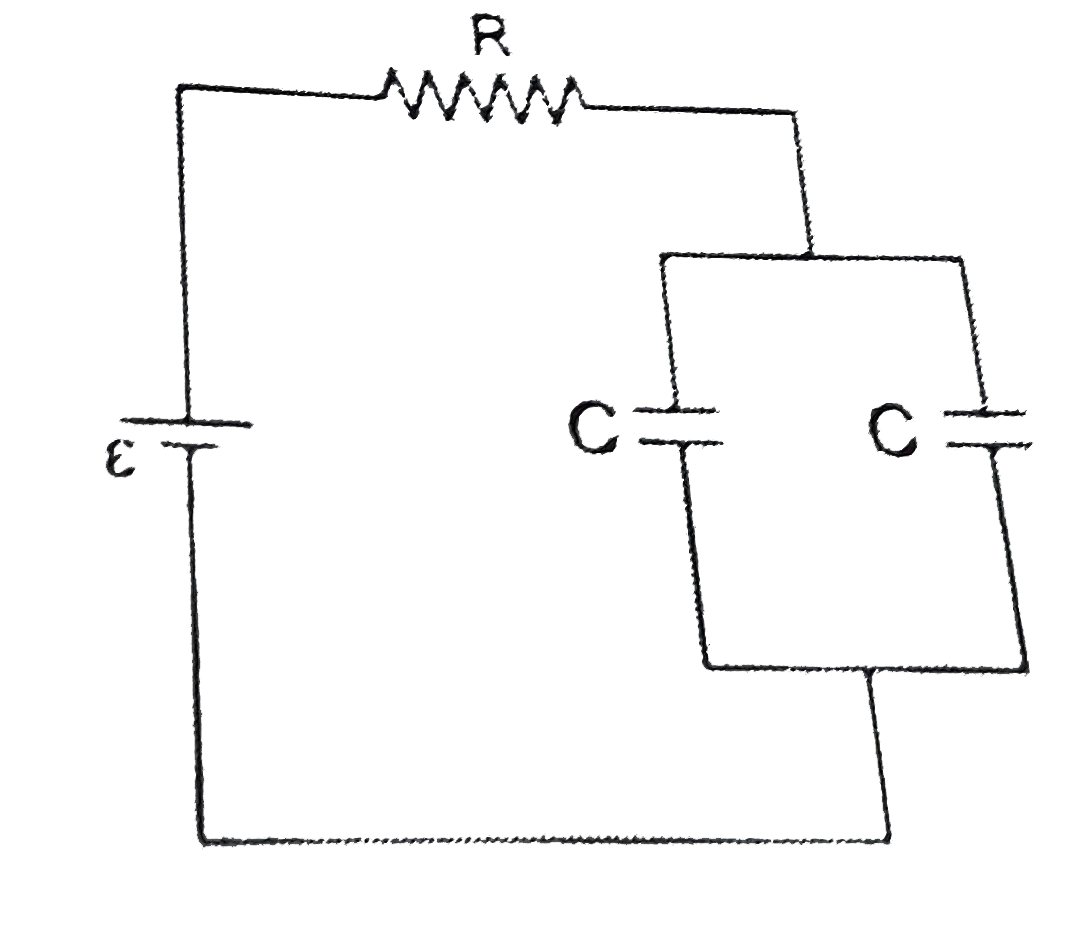
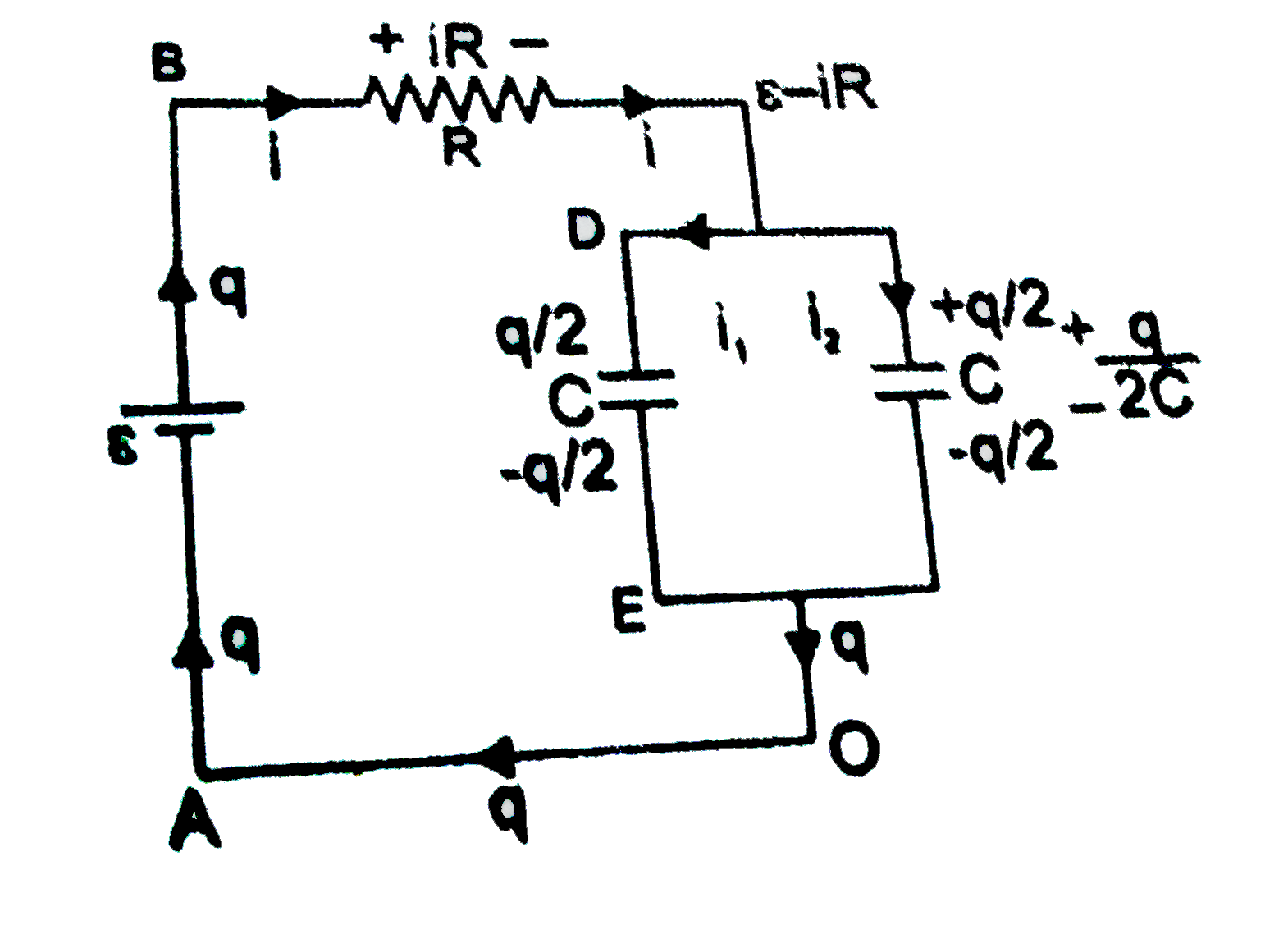
ε−iR=q2C
i=εR−q2RC=2Cε−q2CR
dq2εC−q=dt2CR
∫q0dq(2εC−q)=t2CR
2εC−q2εC=e−t/2RC
q=2εC(1−e−t/2RC)
q1=q2=εC(1−e−t/2RC)⇒i1=ε2Re−t/2RC
q2=q2=εC(1−e−t/2RC)⇒i2=ε2Re−t/2RC
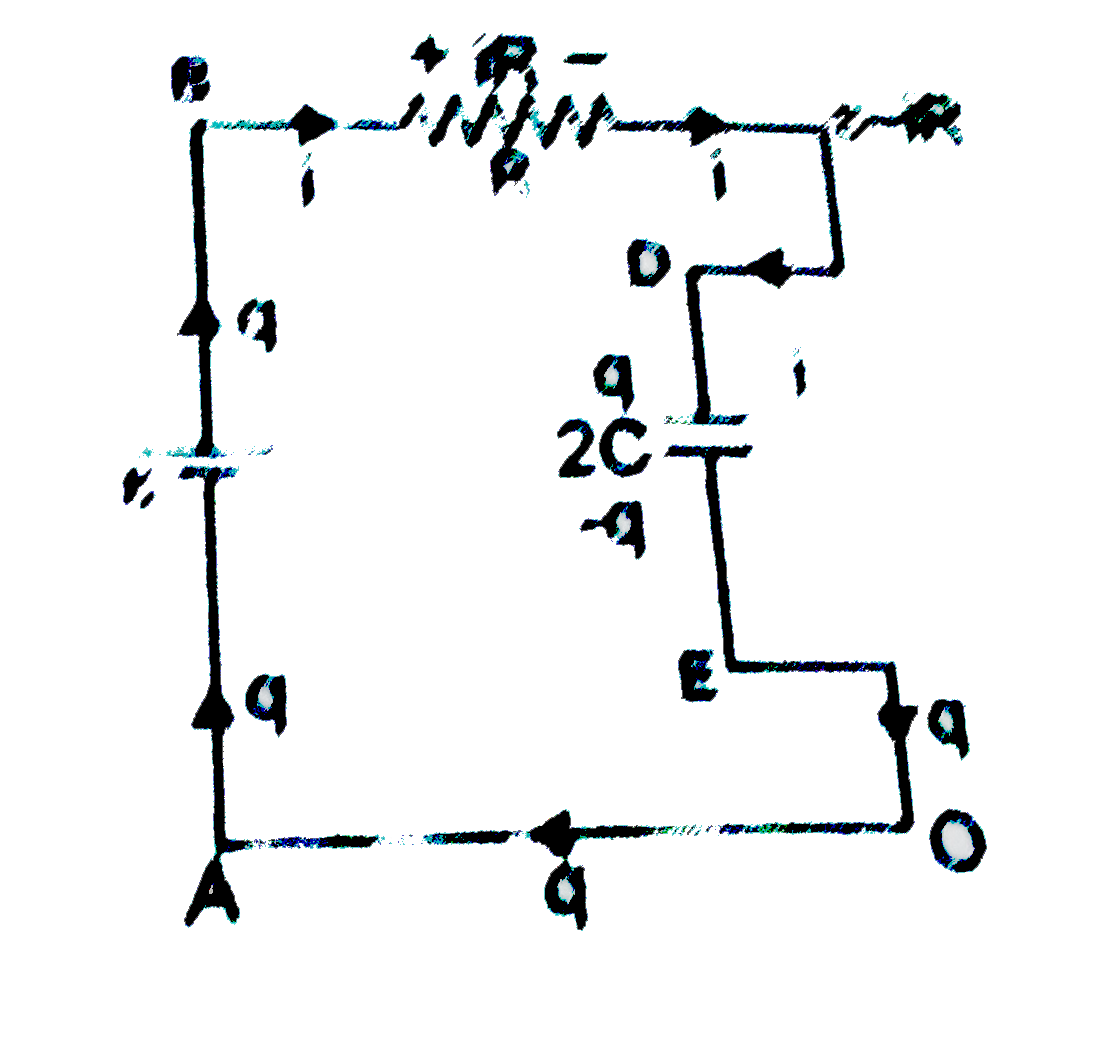
Alternate solution
by equivalent
Time constant of circuit =2C×R=2RC
maximum charge on capacitor =2C×ε=2Cε
Hence equations of charge and current are as given below
q=2εC(1−e−t/2RC)
q1=q2=εC(1−e−t/2CR)⇒i1=ε2Re−t/2CR
q2=q2=εC(1−e−t/2RC)⇒i2=ε2Re−e−t/2RC
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - Miscellaneous Solved Example3videos
CAPACITANCE
- BOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - Exercise - 179videos
CAPACITANCE
- BOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems17videos
ATOMIC PHYSICS
- BOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 313videos
COMMUNICATION SYSTEMS
Similar Questions
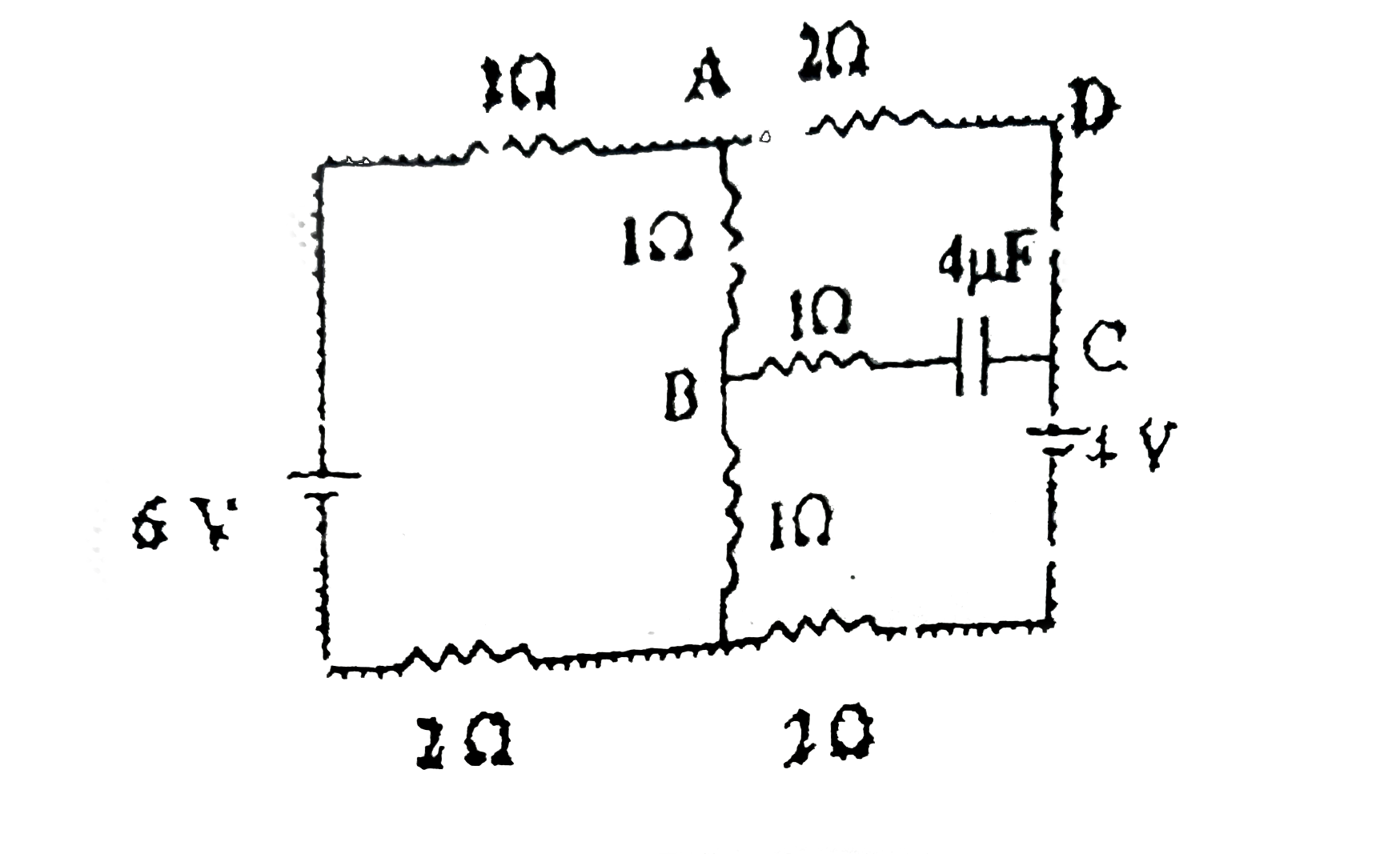
Find the charge on capacitor in steady state.
 View Solution
View SolutionFind the charge on the capacitor shown in figure
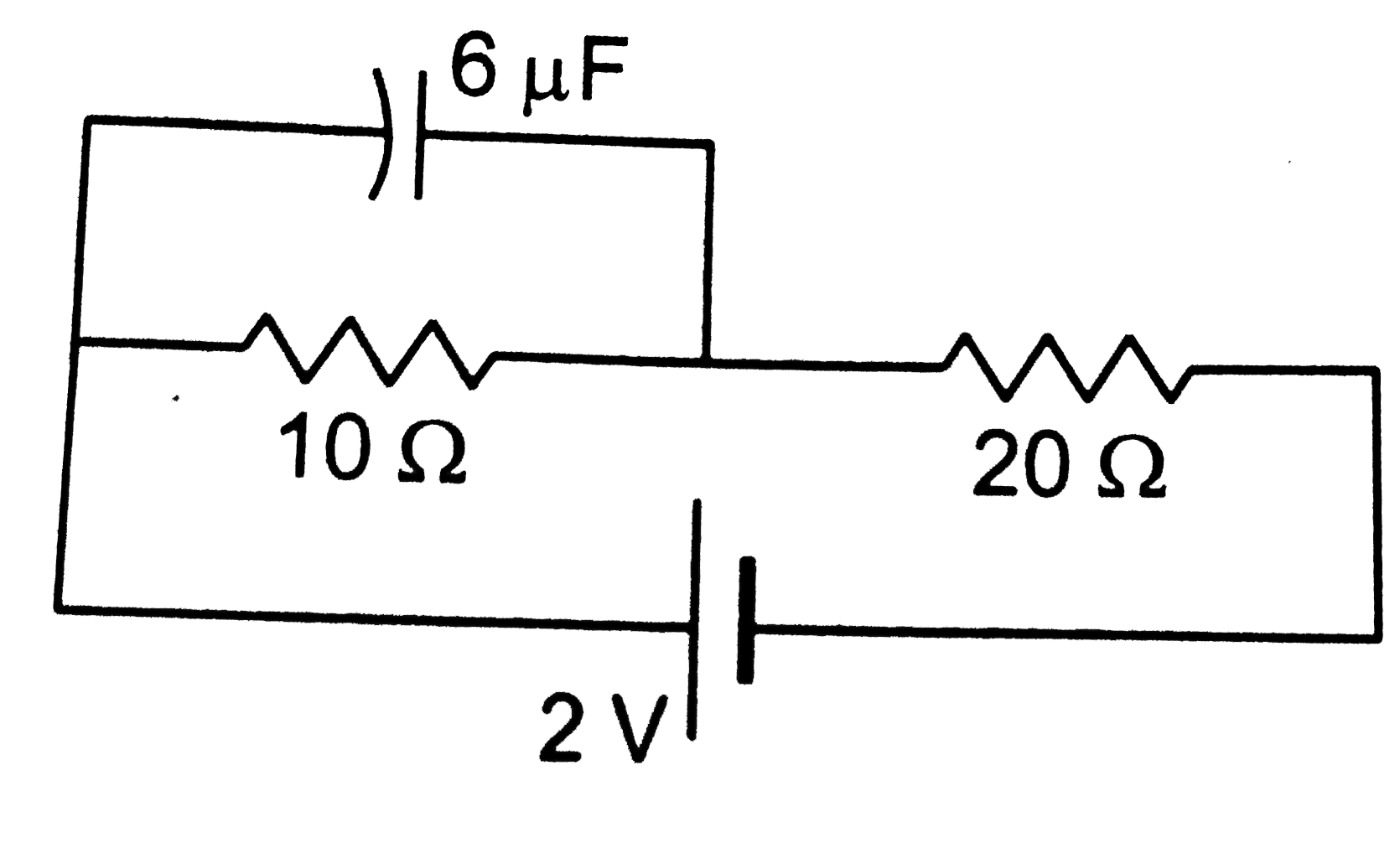 View Solution
View SolutionFind the charge stored in the capacitor.
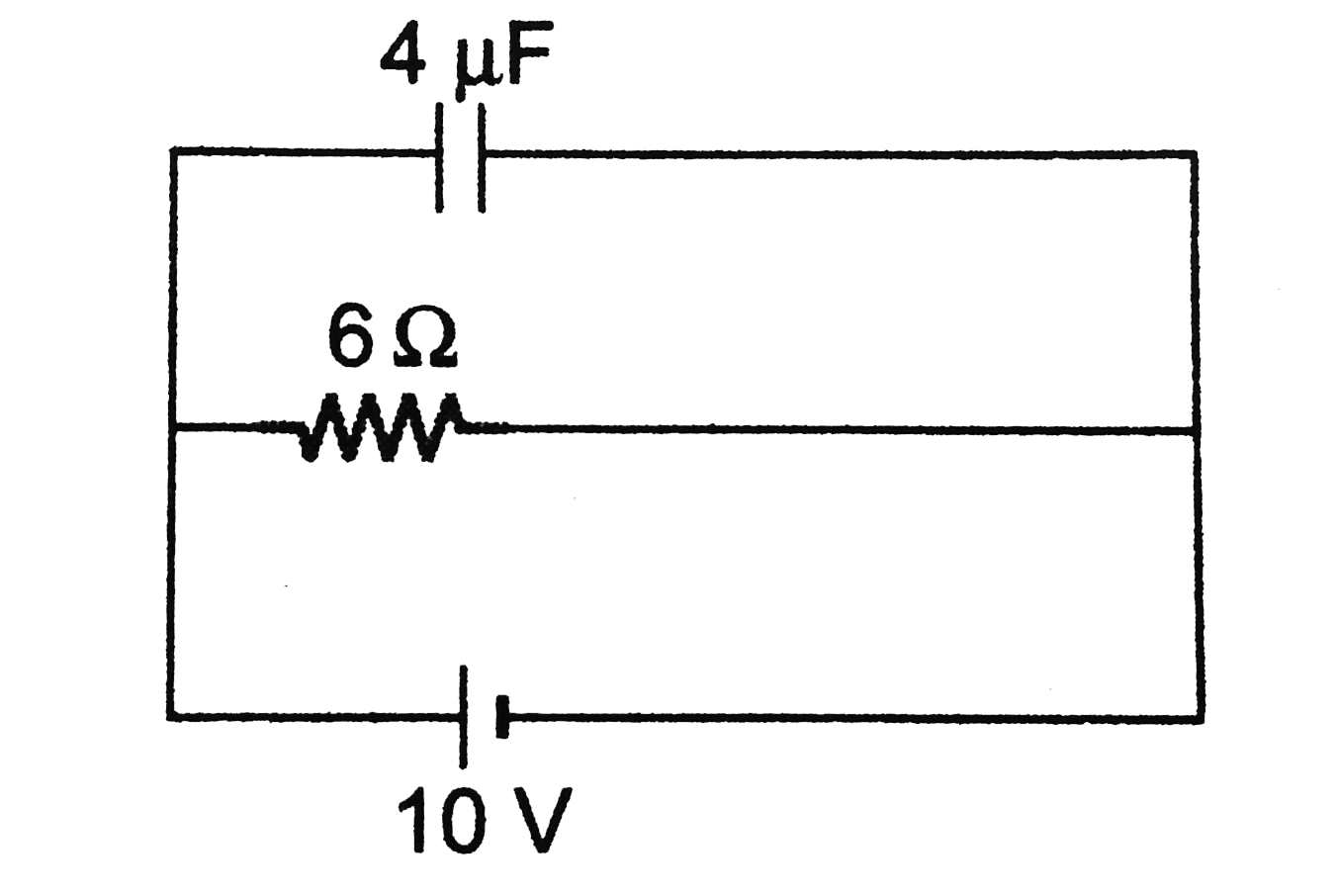 View Solution
View SolutionFind the charge stored in the capacitor.
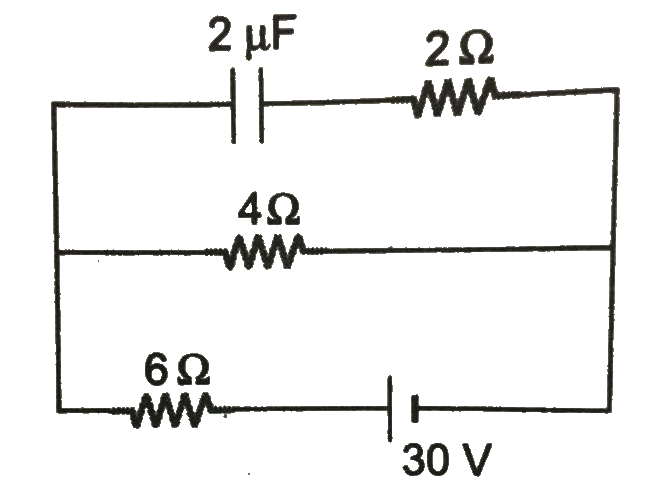 View Solution
View SolutionFind the charge stored in the capacitor.
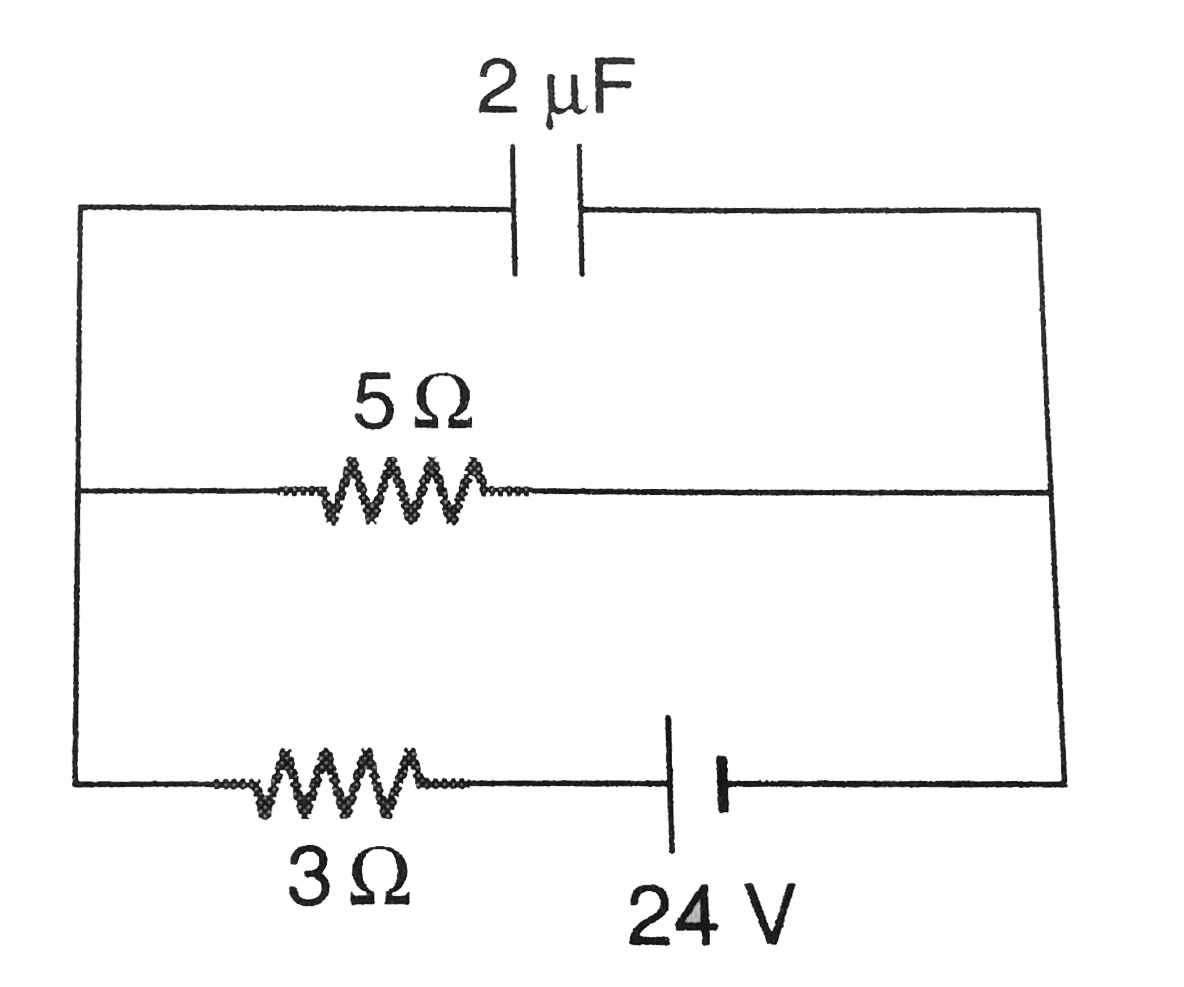 View Solution
View SolutionFind charges on different capacitors.
 View Solution
View SolutionFind charge on each capacitor and potential difference across each capacitor .
 View Solution
View SolutionFind the current in each branches of the circuit.
 View Solution
View SolutionA capacitor of capacitance C is given a charge q0. At time t=0 it is connected to an uncharged capacitor of equal capacitance through a resistance R. Find the charge on the first capacitor and the second capacitor as a function of time t. Also plot the corresponding q-t graphs.
View SolutionConsider a parallel pate capacitor of capactance C with partially conducting medium between its plates having a resistacne Rc if this capacitor is connected to a battery of emf ε and a resistor R as shown in fig.
a. charge on the capacitor as a function of time.
The switch R as a function of time.
 View Solution
View Solution

