Find the potential at point A

Let potential at A=x, applying Kirchhoff current law at junction A
x−20−101+x−15−202+x+301=0
2x−60+x−35+x+45+2x+602=0
⇒6x+10=0⇒x=−5/3
Potential at A=−53V
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Solued miscellaneous Prolblems
8 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-1 (Part-1)
41 Videos
- COMMUNICATION SYSTEMSBOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 3
13 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP.No.71
1 Videos
Similar Questions
The arrangement shows a part of complete circuit. The potentials at point A and B are V1 and V2 respectively . Find the potential at point P.
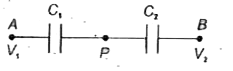
Strategy : The two capacitors C1 and C2 are connected in series . Therefore the charge on both of the capacitors is same . Let the potential at P is V .
View SolutionThe arrangement shows a part of complete circuit . The potentials at points A and B are V1 and V2 respectively . Find the potential at point P .

Strategy : The two capacitors C1 and C2 are connected in series . Therefore the charge on both of the capacitors is same. Let the potential at P is V.
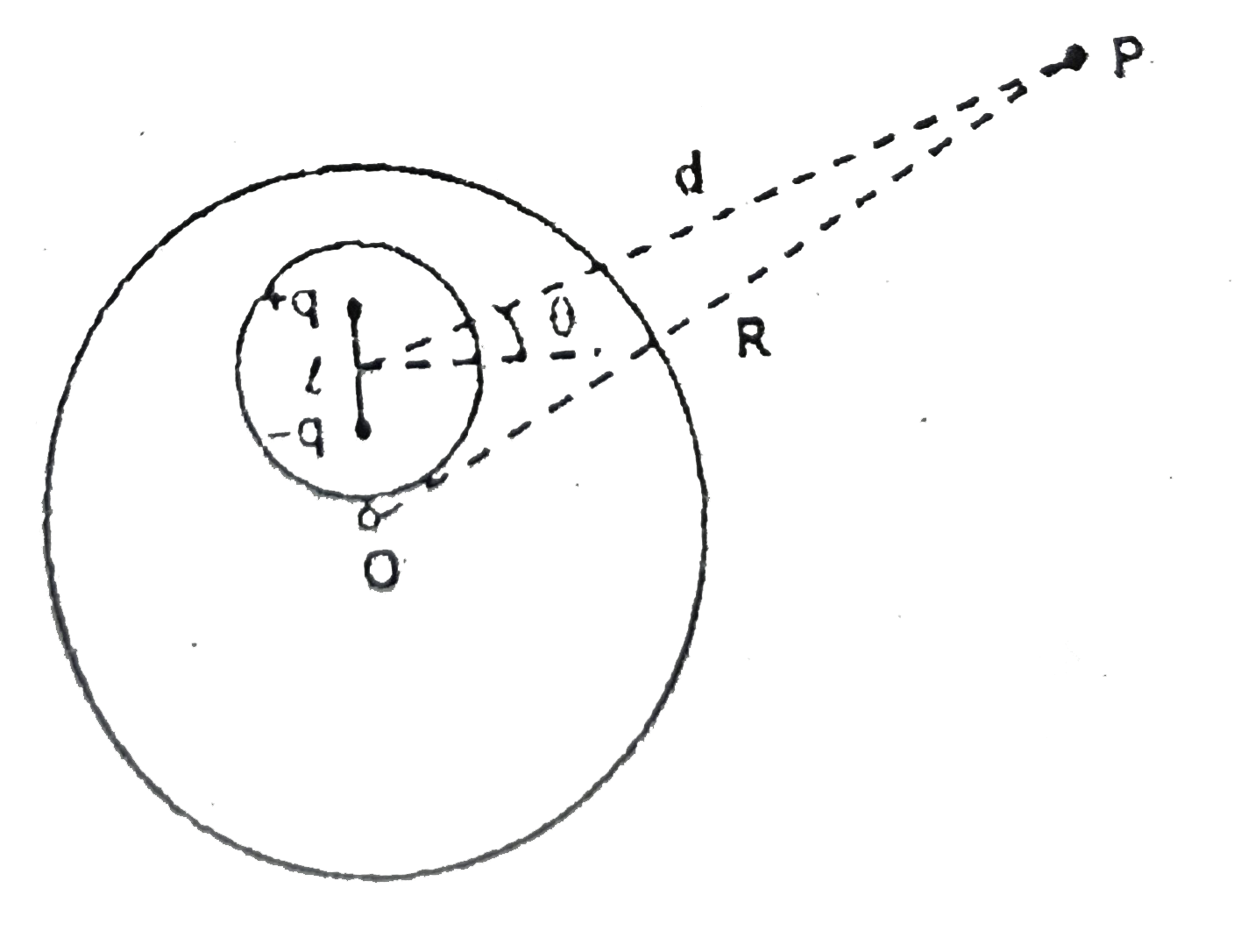
View SolutionA cavity is taken out from a uniform conducting sphere. Inside the cavity a dipole is placed as shown in the figure. Find the potential at point P (in Volt).
(q=10−8C, l=0.1mm, θ=30∘, d=10cm, R=12cm)
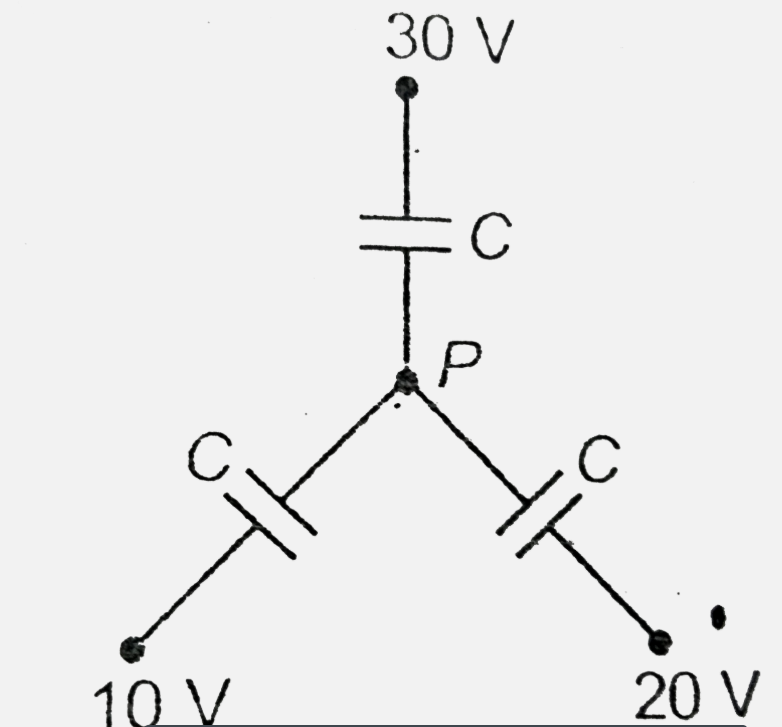
View SolutionFind the potential of point P
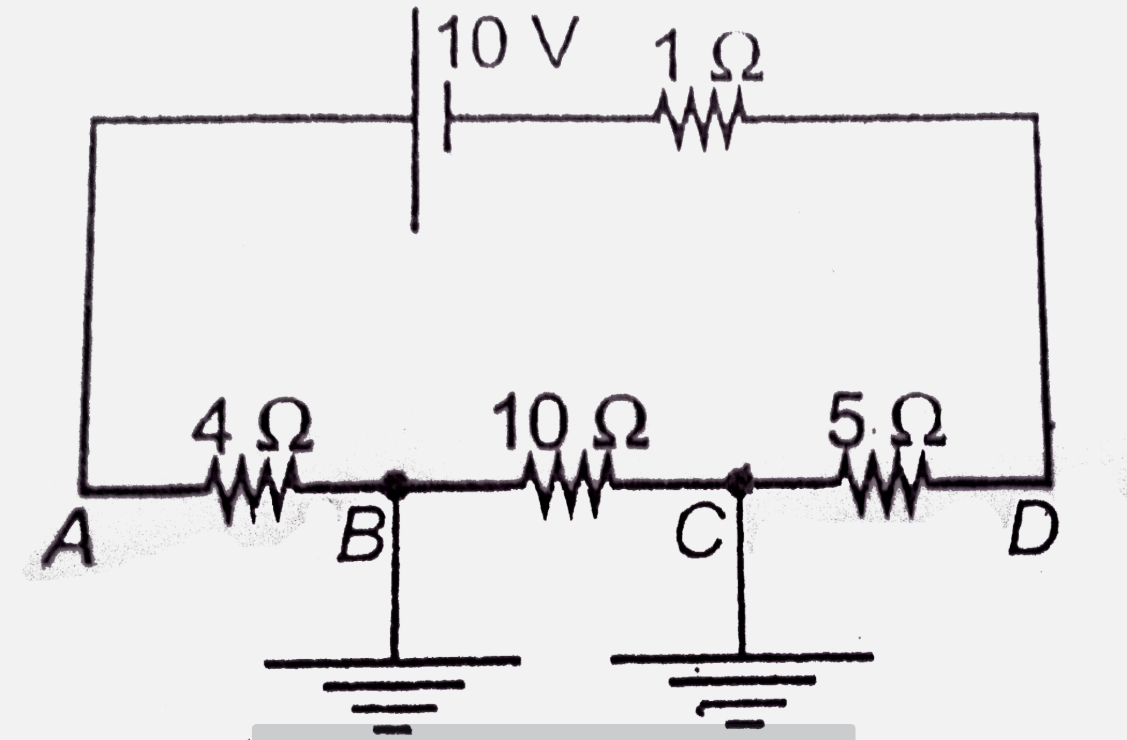
View SolutionIn the electrical circuit shown, points B and C are earthed . Find the potentials of points A and D .
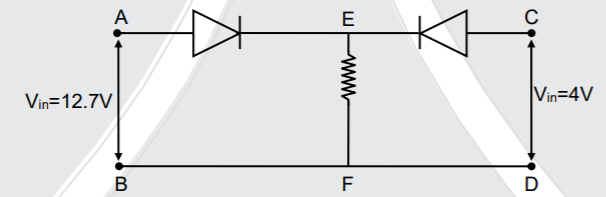
View SolutionIn the given circuit both diodes are ideal having zero forward resistance and built-in potential of 0.7 V. Find the potential of point E in volts.
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionThree spherical shells of masses M, 2M and 3M have radii R, 3R and 4R as shows in figure. Find net potential at point P,
View Solutiontwo point charges 2μC and −4μC are situated at points (−2m,0m) and (2m,0m) respectively. Find out potential at point C(4m,0m) and D(0m,√5m).

View SolutionThe gravitational field due to a mass distribution is given by →l=kx2ˆi, where k is a constant. Assuming the potential to be zero at infinity, find the potential at a point x = a.
View Solution
