A body is moving with variable acceleartion (a) along a straight line. The average acceleration of body in time interval t1 to t2 is :-
a[t2+t1]2
a[t2−t1]2
∫t2t1adtt2+t1
∫t2t1adtt2−t1
The correct Answer is:D
To find the average acceleration of a body moving with variable acceleration a(t) over a time interval from t1 to t2, we can follow these steps:
1. Understanding Average Acceleration:
The average acceleration ¯a over a time interval is defined as the change in velocity divided by the time interval. For variable acceleration, we can express this in terms of integration.
2. Formula for Average Acceleration:
The average acceleration can be calculated using the formula:
¯a=1t2−t1∫t2t1a(t)dt
where a(t) is the acceleration as a function of time.
3. Setting Up the Integral:
We need to evaluate the integral of acceleration a(t) from t1 to t2:
∫t2t1a(t)dt
4. Calculating the Time Interval:
The time interval t2−t1 is simply the difference between the upper and lower limits of the time.
5. Putting It All Together:
Now, substituting the integral and the time interval into the average acceleration formula:
¯a=∫t2t1a(t)dtt2−t1
6. Conclusion:
Thus, the average acceleration of the body in the time interval from t1 to t2 is given by:
¯a=∫t2t1a(t)dtt2−t1
The average acceleration ¯a over a time interval is defined as the change in velocity divided by the time interval. For variable acceleration, we can express this in terms of integration.
The average acceleration can be calculated using the formula:
¯a=1t2−t1∫t2t1a(t)dt
where a(t) is the acceleration as a function of time.
We need to evaluate the integral of acceleration a(t) from t1 to t2:
∫t2t1a(t)dt
The time interval t2−t1 is simply the difference between the upper and lower limits of the time.
Now, substituting the integral and the time interval into the average acceleration formula:
¯a=∫t2t1a(t)dtt2−t1
Thus, the average acceleration of the body in the time interval from t1 to t2 is given by:
¯a=∫t2t1a(t)dtt2−t1
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - B)
33 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - C)
36 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - EXERCISE
29 Videos
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -J (Aakash Challengers Questions)
7 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)
2 Videos
Similar Questions
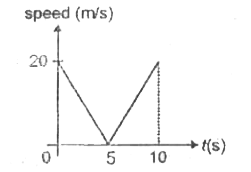
The speed - time graph for a body moving along a straight line is shown in figure. The average acceleration of body may be
View SolutionThe position (x) of a particle moving along x - axis veries with time (t) as shown in figure. The average acceleration of particle in time interval t = 0 to t = 8 s is

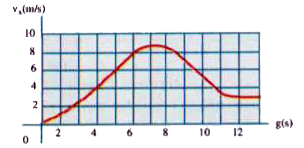
View SolutionGraph of velocity (v) versus time 't' for motion of a motorbike which starts from rest and moves along a stright road is given .
(a)Find the average acceleration for the time interval t0=0 to t1=6.0 s
(b) Estimate the time at which the acceleration has its greatest positive value and the value of the acceleration at that instant.
(c) When is the acceleration is zero ?
(d) Estimate the maximum negative value of the acceleration and the time at which it occurs.
View SolutionAcceleration time graph of a particle moving along a straight line is given. Then average acceleration between t=0 & t=4 is :−

View SolutionThe displacement (in metre) of a particle moving along X-axis is given by x=18t+5t2. The average acceleration during the interval t1=2s and t2=4s is
View SolutionFor a body moving with uniform acceleration along straight line, the variation of its velocity (v) with position (x) is best represented by
View SolutionA body with constant acceleration always moves along a straight line.
A body with constant magnitude of acceleration may not speed up.
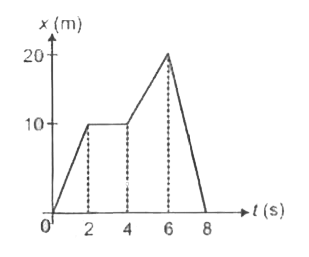
View SolutionThe position (x) - time (t) graph for a particle moving along a straight line is shown in figure. The average speed of particle in time interval t = 0 to t = 8 s is
View SolutionA body is moving with a velocity 5m/s along a striaght line.A force of 10N is applied to the body perpendicular to the line of motion. If the body is of mass 2kg, then the acceleration of the body along the initial straight line of motion is :
View SolutionThe velocity of a particle are given by (4t–2) ms–1 along x–axis. Calculate the average acceleration of particle during the time interval from t = 1 to t = 2s.
View Solution
