Acceleration of a particle has a value 'a' for a time t. It is followed immediately by a retardation of magnitude 'a' for time t/2. Consider this as one cycle. Initial velocity of particle was zero. The displacement of the particle after n such cycles in succession is:
(a)n(3n+4)8at2
(b)n(n+1)2at2
(c)(n2+n+1)4at2
(d)nat2
The correct Answer is:A
To solve the problem, we need to analyze the motion of the particle during one complete cycle of acceleration and retardation. Let's break it down step by step.
Step 1: Analyze the motion during one cycle
1. Acceleration phase: The particle accelerates with an acceleration 'a' for a time 't'.
- Initial velocity (u) = 0
- Final velocity (v) after time 't' can be calculated using the equation:
v=u+at=0+at=at
2. Retardation phase: The particle then decelerates (retardation) with a magnitude 'a' for a time of t2.
- Initial velocity for this phase = at
- Final velocity (v') after t2 can be calculated as:
v′=v−at′=at−a(t2)=at−at2=at2
Step 2: Calculate the displacement during one cycle
1. Displacement during the acceleration phase:
- Using the formula for displacement (s) during uniform acceleration:
s1=ut+12at2=0+12at2=12at2
2. Displacement during the retardation phase:
- Using the same formula for displacement during uniform retardation:
s2=vt′−12a(t′)2=at(t2)−12a(t2)2
- Substituting t′=t2:
s2=at22−12a(t24)=at22−at28=4at28−at28=3at28
3. Total displacement in one cycle:
- The total displacement S in one complete cycle is:
S=s1+s2=12at2+38at2=48at2+38at2=78at2
Step 3: Calculate total displacement after n cycles
- The total displacement after n cycles is:
Sn=n⋅S=n⋅78at2=7n8at2
Final Answer
The displacement of the particle after n cycles is:
Sn=7n8at2
1. Acceleration phase: The particle accelerates with an acceleration 'a' for a time 't'.
- Initial velocity (u) = 0
- Final velocity (v) after time 't' can be calculated using the equation:
v=u+at=0+at=at
- Initial velocity for this phase = at
- Final velocity (v') after t2 can be calculated as:
v′=v−at′=at−a(t2)=at−at2=at2
1. Displacement during the acceleration phase:
- Using the formula for displacement (s) during uniform acceleration:
s1=ut+12at2=0+12at2=12at2
- Using the same formula for displacement during uniform retardation:
s2=vt′−12a(t′)2=at(t2)−12a(t2)2
- Substituting t′=t2:
s2=at22−12a(t24)=at22−at28=4at28−at28=3at28
- The total displacement S in one complete cycle is:
S=s1+s2=12at2+38at2=48at2+38at2=78at2
- The total displacement after n cycles is:
Sn=n⋅S=n⋅78at2=7n8at2
The displacement of the particle after n cycles is:
Sn=7n8at2
Topper's Solved these Questions
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE MAIN (archive)
19 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)
14 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - LEVEL 1
75 Videos
- JEE MAIN REVISON TEST-23BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISON TEST-23EXERCISE - PHYSICS (SECTION 2)
1 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
Similar Questions
Knowledge Check
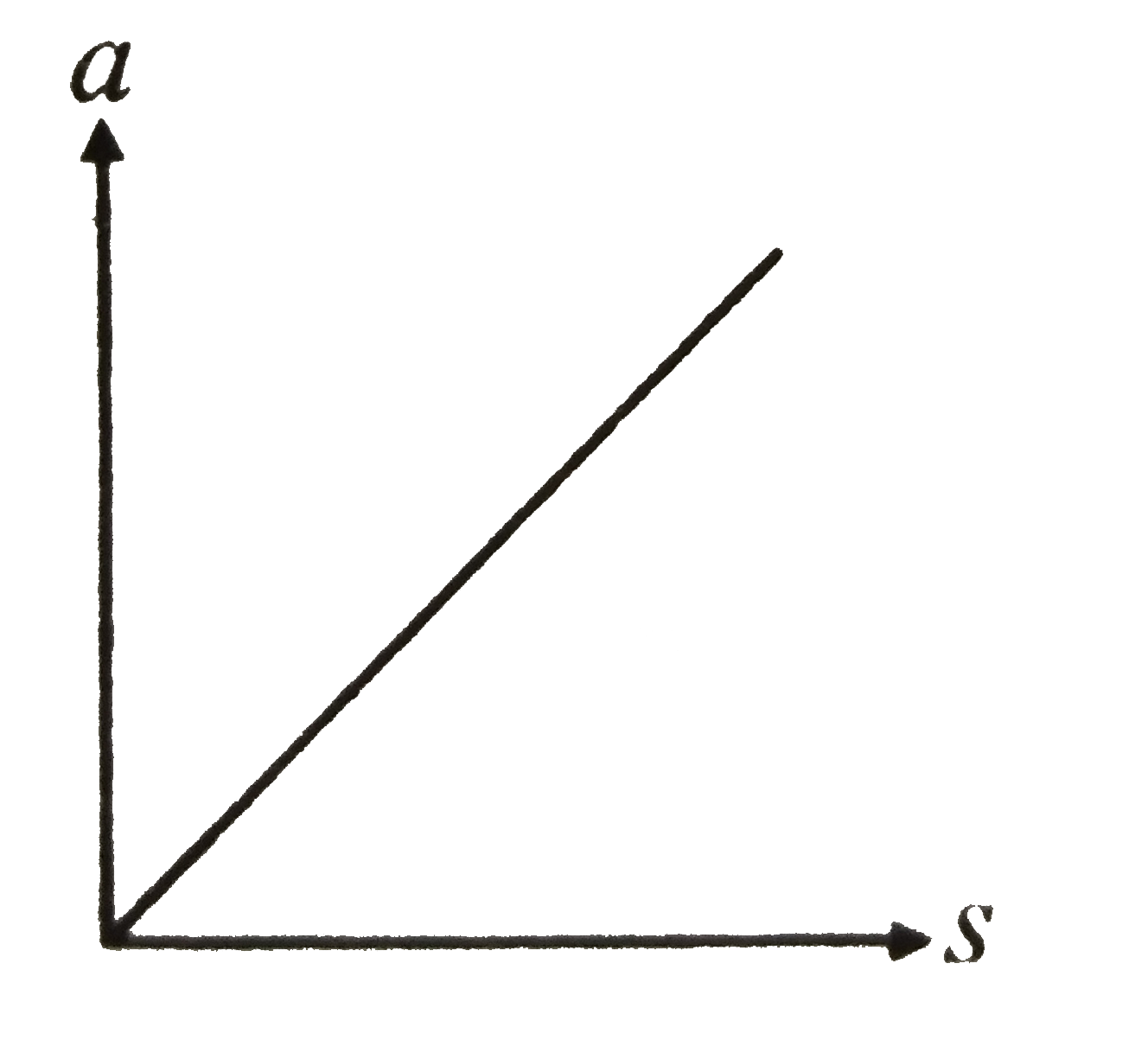
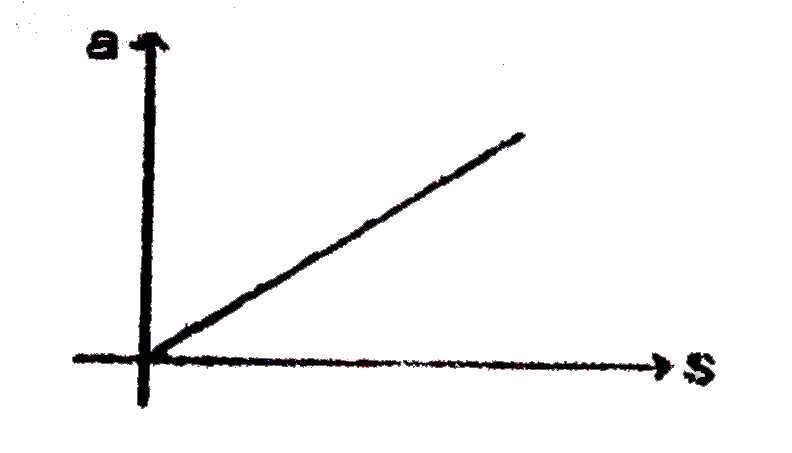
Acceleration (a)-displacement(s) graph of a particle moving in a straight line is shown here. The initial velocity of the particle is zero. The v-s graph of the particle would be
 A
A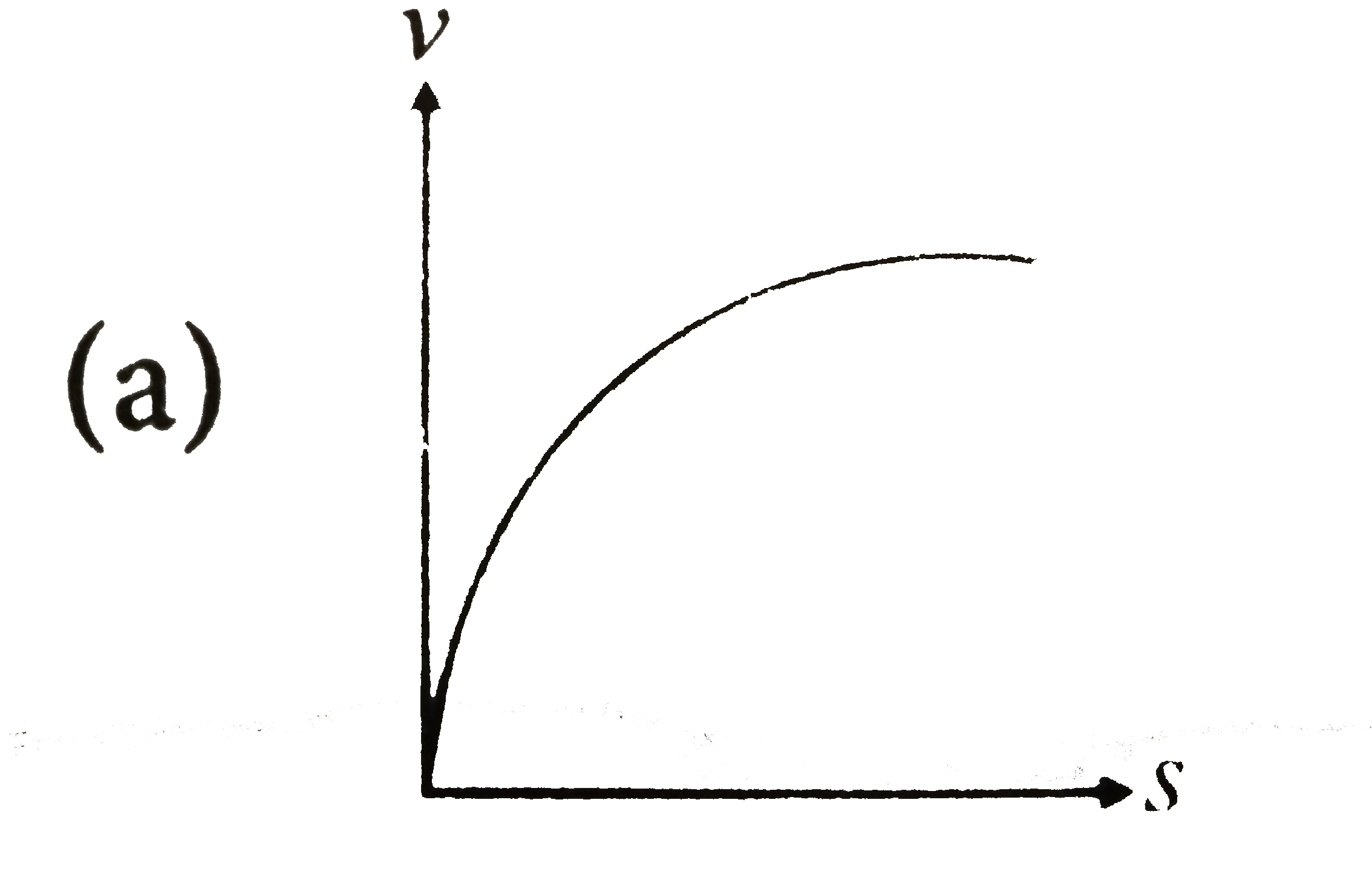 B
B C
C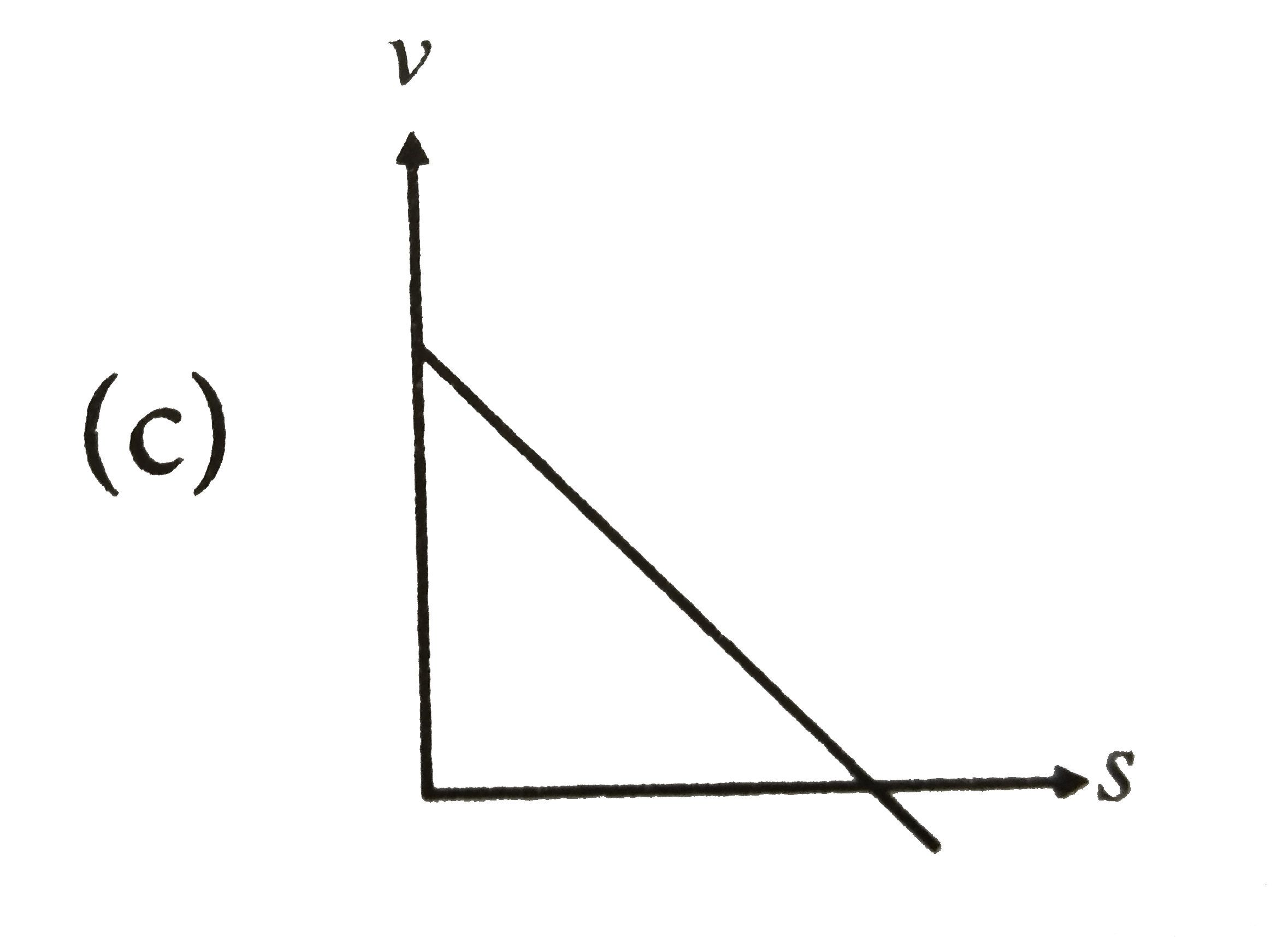 D
D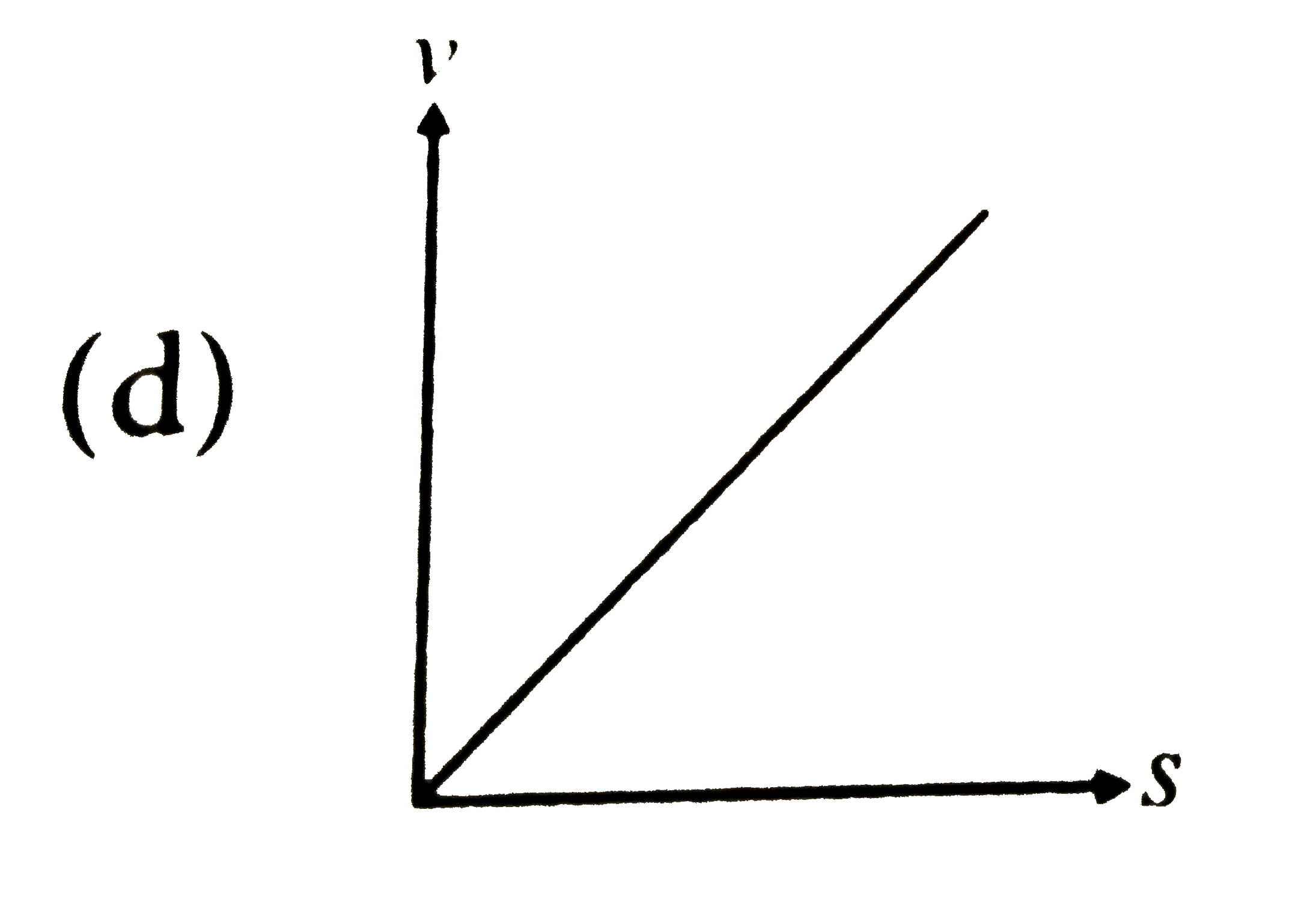
Velocity of a particle varies with time as v=4t. Calculate the displacement of particle between t=2 to t=4 sec.
View SolutionA particle is executing simple harmonic motion with an amplitude A and time period T. The displacement of the particles after 2T period from its initial position is
View SolutionThe acceleration of paticle varies with time as :
a(t)=3t2+4
If the initial velocity of particle is 2m/s, find the velocity of particle at t=3sec.
View SolutionAcceleration (a) -displacement (s) graph of a particle moving in a straight line is as shown in the figure. The initial velocity of the particle is zero. The v−s graph of the particle would be
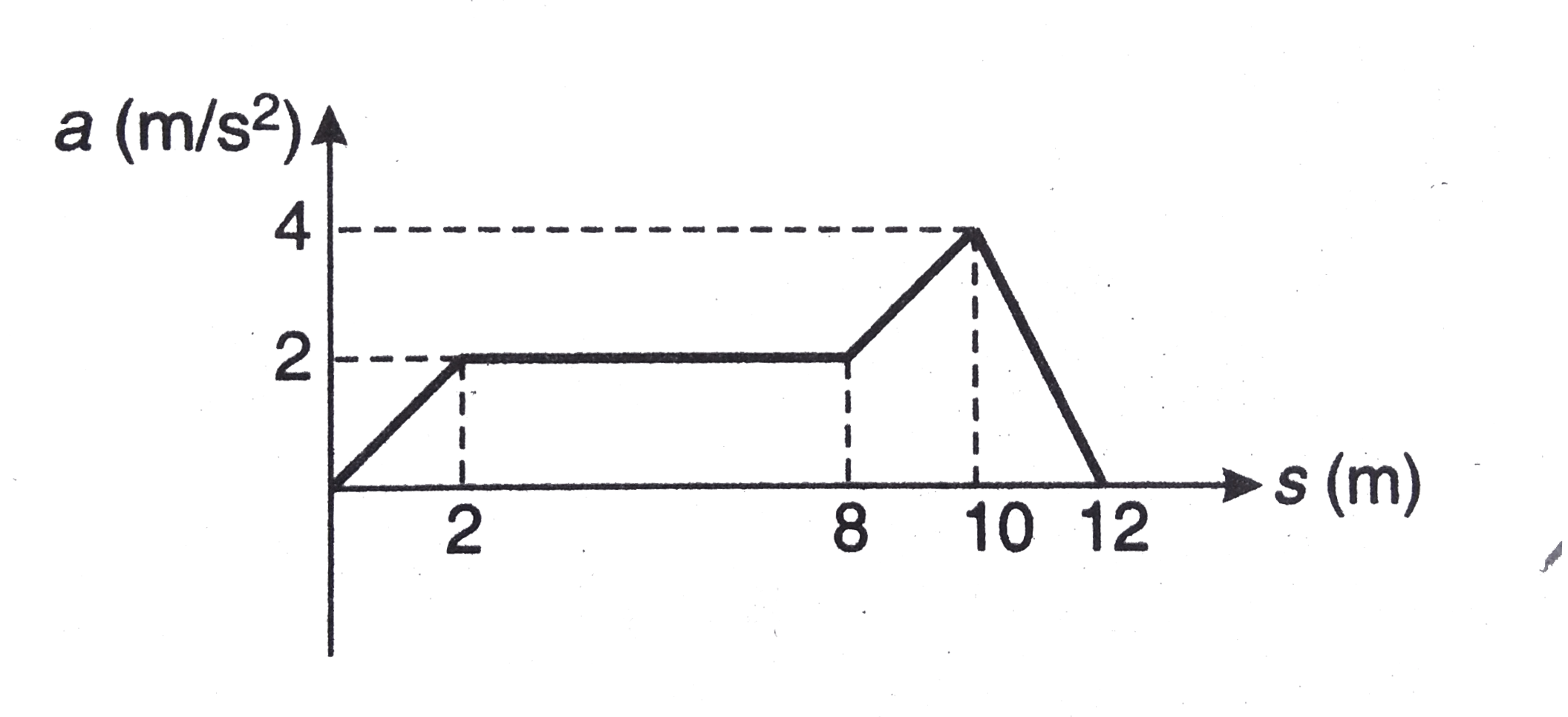
View SolutionThe acceleration-displacement graph of a particle moving in a straight line is as shown in figure, initial velocity of particle is zero. Find the velocity of the particle when displacement of the particle is s=12m.
View SolutionThe acceleration of a particle at time is given by A=−aω2sinωt. Its displacement at time t is
View SolutionIf acceleration a(t)=3t2 and initial velocity u=0 m/s , then the velocity of the particle after time t=4 s
View Solution

 .
.