A resistance of 2Ω is connected across one gap of a meter bridge (the length of the wire is 100cm) and an unknown resistance, greater than 2Ωis conneted across the other gap. When these resistances are interchanged, the balance point shifts by 20cm. Neglecting any corrections,the unknown resistance is
3Ω
4Ω
5Ω
6Ω
R>2Ω∴100−x>x
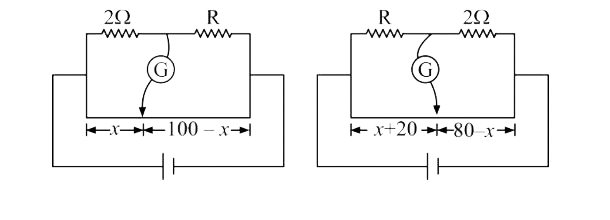
Applying PQ=RS
We have, 2R=x100−x………(i)
R2=x+2080−x…..(ii)
On solving equation (i) and (ii) we get R=3Ω
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-1 JEE MAIN ARCHIVE93videos
DC CIRCUIT
- BOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F10videos
CURRENT ELECTRICITY
- BOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )31videos
DYNAMICS OF A PARTICLE
Similar Questions
A resistance of 2Ω is connected across one gap of a meter bridge (the length of the wire is 100cm and an unknown resistance, greater than 2Ω, is connected across the other gap. When these resistance are interchanged, the balance point shifts by 20cm. Neglecting any corrections, the unknown resistance is.
(a)3Ω
(b) 4Ω
( c) 5Ω
(d) 6Ω.View SolutionResistance in the two gaps of a meter bridge are 10ohm and 30ohm respectively. If the resistances are interchanged he balance point shifts by
View Solution
Knowledge Check
- Question 1 - Select One
Two resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
A3B6C9D12
In the metre bridge, the balancing length AB = 20 cm. The unknown resistance X is equal to
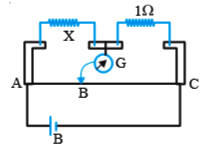 View Solution
View SolutionAn unknown resistance R1 is connected is series with a resistance of 10Ω. This combination is connected to one gap of a meter bridge, while other gap is connected to another resistance R2. The balance point is at 50cm Now , when the 10Ω resistance is removed, the balanced point shifts to 40cm Then the value of R1 is.
View SolutionAn unknown resistance R1 is connected is series with a resistance of 10Ω. This combination is connected to one gap of a meter bridge, while other gap is connected to another resistance R2. The balance point is at 50cm Now , when the 10Ω resistance is removed, the balanced point shifts to 40cm Then the value of R1 is.
View SolutionIn a metre bridge, the length of the wire is 100 cm. At what position will the balance point be obtained if the two resistances are in the ratio 2 : 3?
View SolutionIn the metre bridge, the balancing length AB =l=20 cm. The unknown resistance X is equal to
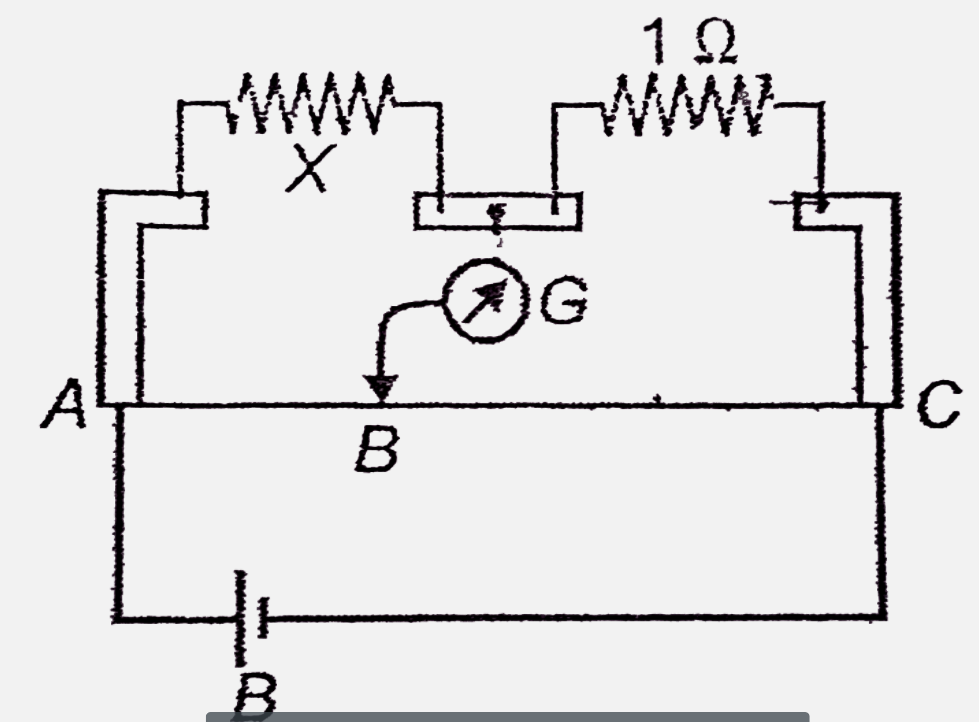 View Solution
View SolutionTwo resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
View SolutionTwo resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
View Solution

