A uniform disk turns at 2.4rev/s around a frictionless axis. A nonrotating rod, of the same mass as the disk and length equal to the disk's diameter is dropped onto the freely spinning disk (see the figure). They then both turn around the axis with their centres superposed. What will be the angular frequency in rev/s of the combination when they start rotating together.
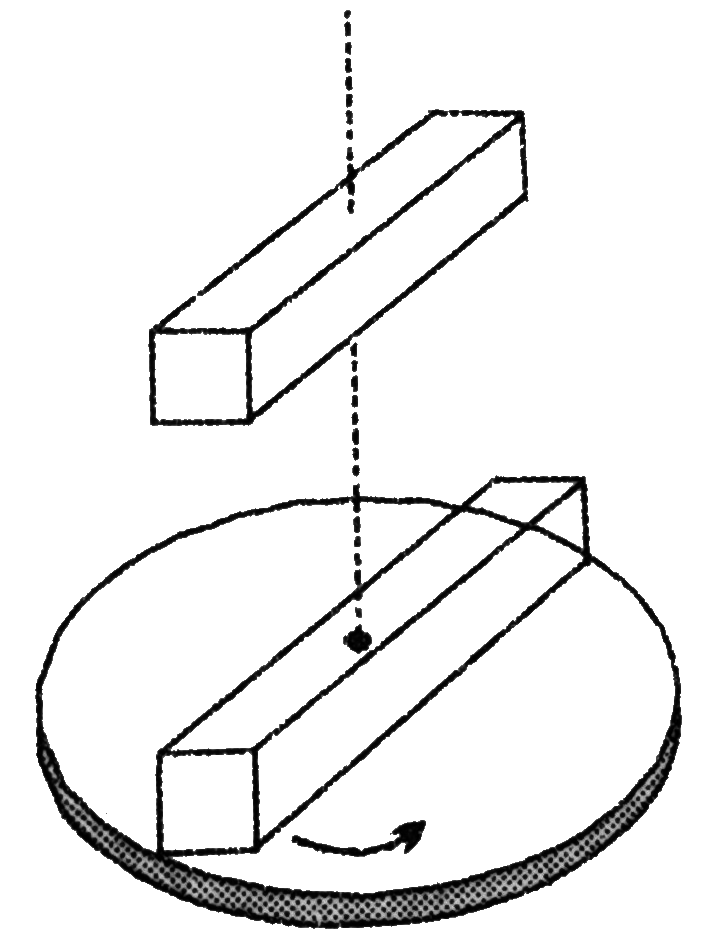
The correct Answer is:(1.44)
I1ω1=I2ω2
⇒ω2=I1I2ω1=mr2/2mr2/2+m(2r)212ω1
⇒ω2=1/21/2+1/3×2.4=1/25/6×2.4=1.44 rev/sec.
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 2 (Rotatinal Kinematics, Moment of Inertia)
10 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 2 (Torque, Fixed and Rotation)
10 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 1 (Mixed topics)
15 Videos
- REVISION TEST-2 JEEBOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS
25 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
Similar Questions
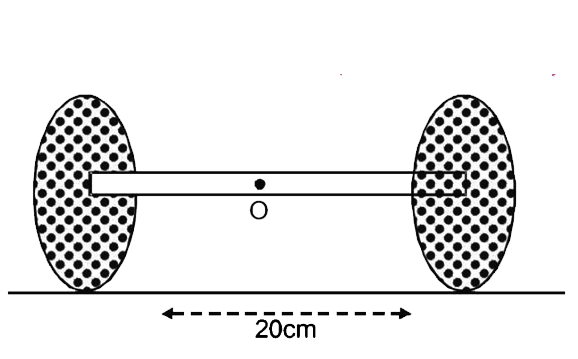
Two thin circular disks of mass 2kg and radius 10 cm each are joined by a rigid massless rod of length 20 cm. the axis of the rod is along the perpendicular to the planes of the disk through their centres. This object is kept on a truck in such a way that the axis of the object is horizontal and perpendicular to the direction of the motion of the truck. Its friction with the floor of the truck is large enough so that the object can roll on the truck without slipping. Take x axis as the direction of motion of the truck and z-axis as the vertically upwards direction. if the truck has an acceleration of 9m/s2 Calculate:
(i) The force fo friction on each disk,
(ii) The magnitude and the direction of the frictional torque acting on each disk about the centre of mass O of the object. Express the torque in the vector form in terms of unit vectors ˆi,ˆjandˆk in the x,y, and z directions.
View SolutionA uniform disk, a thin hoop (ring), and a uniform sphere, all with the same mass and same outer radius, are each free to rotate about a fixed axis through its center. Assume the hoop is connected to the rotation axis by light spokes. With the objects starting from rest, identical forces are simultaneously applied to the rims, as shown. Rank the objects according to their angular momentum after a given time t, least to greatest.

View SolutionA uniform disc of mass 20 kg and radius 0.5 m can turn about a smooth axis through its centre and perpendicular to the disc. A constant torque is applied to the disc for 3s from rest and the angular velocity at the ned of that time is 240πrev/min find the magnitude of the torque. if the torque is then removed and the disc is brought to rest in t seconds by a constant force of 10 N applied tangentially at a point on the rim of the disc, find t
View SolutionA uniform disk of mass 300kg is rotating freely about a vertical axis through its centre with constant angular velocity ω. A boy of mass 30kg starts from the centre and moves along a radius to the edge of the disk. The angular velocity of the disk now is
View SolutionA uniform rod of mass 300 g and length 50 cm rotates at a uniform angular speed of 2 rad/s about an axis perpendicular to the rod through an end. Calculate a. the angular momentum of the rod about the axis of rotation b. the speed of the centre of the rod and c. its kinetic energy.
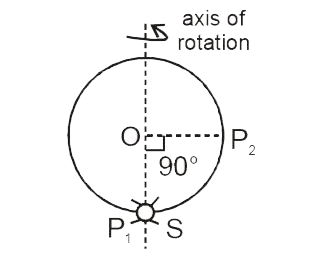
View SolutionA uniform ring is rotating about vertical axis with angular velocity ω initially. A point insect (S) having the same mass as that of the ring starts walking from the lowest point P1 and finally reaches the point P2 (as shown in figure). The final angular velocity of the ring will be equal to
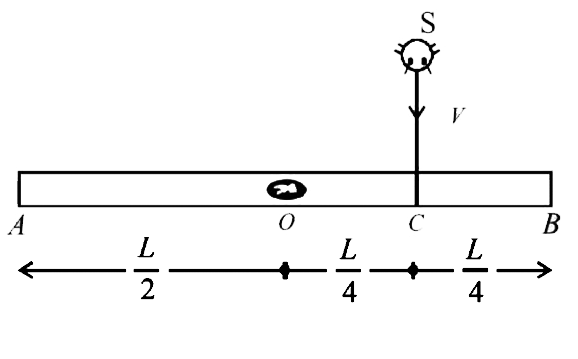
View SolutionA homogeneous rod AB of length L = 1.8 m and mass M is pivoted at the center O in such a way that it can rotate it can rotate freely position. An insect S of the same mass M falls vertically with speed V on the point C, midway between the points O and B. Immediately after falling, the insect moves towards the end B such that the rod rotates with a constant angular velocity omega.
(a) Determine the angular velocity ω in terms of V and L.
(b) If the insect reaches the end B when the rod has turned through an angle of 90∘, determine V.
View SolutionA disk of mass M(=2 kg) and radius R(=5m) is pivoted at the centre.
The disk liess in the vertical plane and is free to rotate about the pivot (see figure) . A particle of mass m(=1 kg) is on the periphery of the disk as shown in the figure. The time period of small oscillation of the system is [Taking g=10m/s2]

View SolutionA metal rod of length 'L' and mass 'm' is piovted at one end. A thin disk of mass 'M' and radius 'R'(<L). Is attached at its centre to the free end of the rod. Consider two ways the disc is attached: (case A). The disc is not free to rotate about its centre and (case B) the disc is free to rotate about its center. The rod-disc sustem perform SHM in vertical plane after being released from the same displaced potion. Which of the following statement(s) is (are) true?
View SolutionA massless rod S having length 2l has equal point masses attached to its two ends as shown in figure. The rod is rotating about an axis passing through its centre and making angle α with the axis. The magnitude of change of momentum of rod i.e., ∣∣∣dLdt∣∣∣ equals
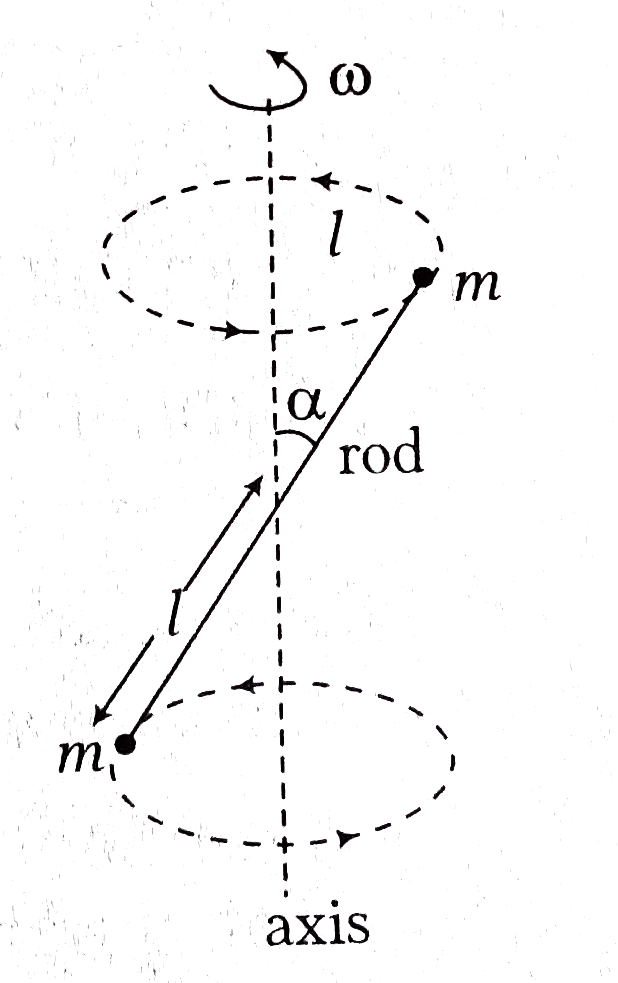
View Solution
