Four point charges +8μC−1μC,−1μCand+8μC are fixed at the points −√27/2m,−√3/2m+√3/2mand+√27/2m respectively on the Y-axis. A particle of mass 6×10−4 kg and charge +0.1μC moves along the -X direction. It speed at x=+∞ is v0. Find the least value of v0 for which the paticle will cross the origin. Find also the kinetic energy of the particle at the origin. Assume that space is gravity free.
The correct Answer is:(v0=3m/s,x=3)
(V0=3m/s,x=3)
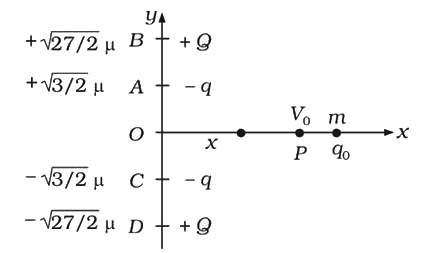
In the figure q=1μC=10−6C,q0=+0.1μC=10−7C and m=6×10−4Kg and Q =8μC
Let P be any point at a distance x from origin O . Then
AP=CP=√32+X2
BP=DP=√272+x2
Electric potential at point P will be, V=2KQBP−2kqAP
Where K=14πε0=9×109Nm/C2
∴ V=2×9×109⎡⎢
⎢⎣8×10−6√272+x2+√32+x2⎤⎥
⎥⎦,v=1.8×104⎡⎢
⎢⎣8√272+x−1√32+x2
Electric field at P
E=−dVdx=1.8×104[(β)(−12)(272+x2)−3/2(−12)(32+x2)−3/2](2x)
E = 0 on x-axis where x = 0 or 8(272+x2)3/2=1(32+x2)3/2
⇒(4)3/2(272+x2)3/2=132+x2⎞⎟
⎟
⎟⎠3/2⇒(272+x2)=4(32+x2)
This equation gives x=±√52m
The least value of kinetic energy of the particle at infinity should be enough to take the particle upto x=±√52 m because at x=+√52m,E=0 . ⇒ Electrostatic force on charge q is zero or Fe=0
For at x>√52m E is repulsive ( towards positive x - axis) & for x>√5m, E is attractive (towards negative x axis). Now form Eq (i) potential at x=√52m.
V=1.8×104⎡⎢
⎢⎣8√272+52−1√32+52⎤⎥
⎥⎦,v0=√2q0Vm
Substituting the value
V0=√2×10−7×2.7×1046×10−4⇒v0=3m/s∴Minimum value of v0 is 3m/s
From Eq (i) , potential orgin ( x = 0) is , v0=1.8×104⎡⎢
⎢⎣8√272−1√32=2.4×104V
Let be the kinetic energy of the particle at origin. Applying energy conservation at and at k+q0v0=12mv20
But 12mv20=q0V [ form Eq (i)]
k=q0(V−V0) ,
k=(10−7)(2.7×10−4−2.4×104) , k=3×10−4J
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE MAIN65videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE52videos
ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE1videos
ENERGY & MOMENTUM
Similar Questions
Four point charges +8μC,−1μC,−1μC and , +8μC are fixed at the points −√27/2m,−√3/2m,+√3/2m
and +√27/2m respectively on the y-axis. A particle of mass 6×10−4kg and +0.1μC moves along the x-direction. Its speed at x=+∞ is v0. find the least value of v0 for which the particle will cross the origin. find also the kinetic energy of the particle at the origin in tyhis case. Assume that there is no force part from electrostatic force.View Solutiontwo point charges 2μC and −4μC are situated at points (−2m,0m) and (2m,0m) respectively. Find out potential at point C(4m,0m) and D(0m,√5m).
 View Solution
View SolutionElectric charges of +10μC,+5μC,−3μCand+8μC are placed at the corners of a square of side √2 m, the potential at the centre of the square is
View SolutionTwo point charges 3μC and 2.5μC are placed at point A (1, 1, 2)m and B (0, 3, -1)m respectively. Find out electric field intensity at point C(3, 3, 3)m.
View SolutionA particle of mass 100 gm and charge 2μC is released from a distance of 50 cm from a fixed charge of 5μC. Find the speed of the particle when its distance from the fixed charge becomes 3 m.
View SolutionA particle of mass 2 g and charge 1μC is held at rest on a frictionless surface at a distance of 1m from a fixed charge of 1 mC. If the particle is released it will be repelled. The speed of the particle when it is at distance of 10 m from fixed charge is :
View SolutionThree point charge q1=1μC,q2=−2μC and q3=3μC are placed at (1m,0,0),(0,2m,0) and (0,0,3m) respectively. Find the electric potential at as origin.
View SolutionElectric charge of 1μC,−1μC and 2μC are placed in air at the corners A, B and C respectively of an equilateral triangle ABC having length of each side 10 cm. The resultant force on the charge at C is
View SolutionTwo point charges q1=q2=2μC are fixed at x1=+3m and x2=−3m as shown in figure. A third particle of mass 1 g and charge q3=−4μC are released from rest at y=4.0m.Find the speed of the particle as it reaches the origin.
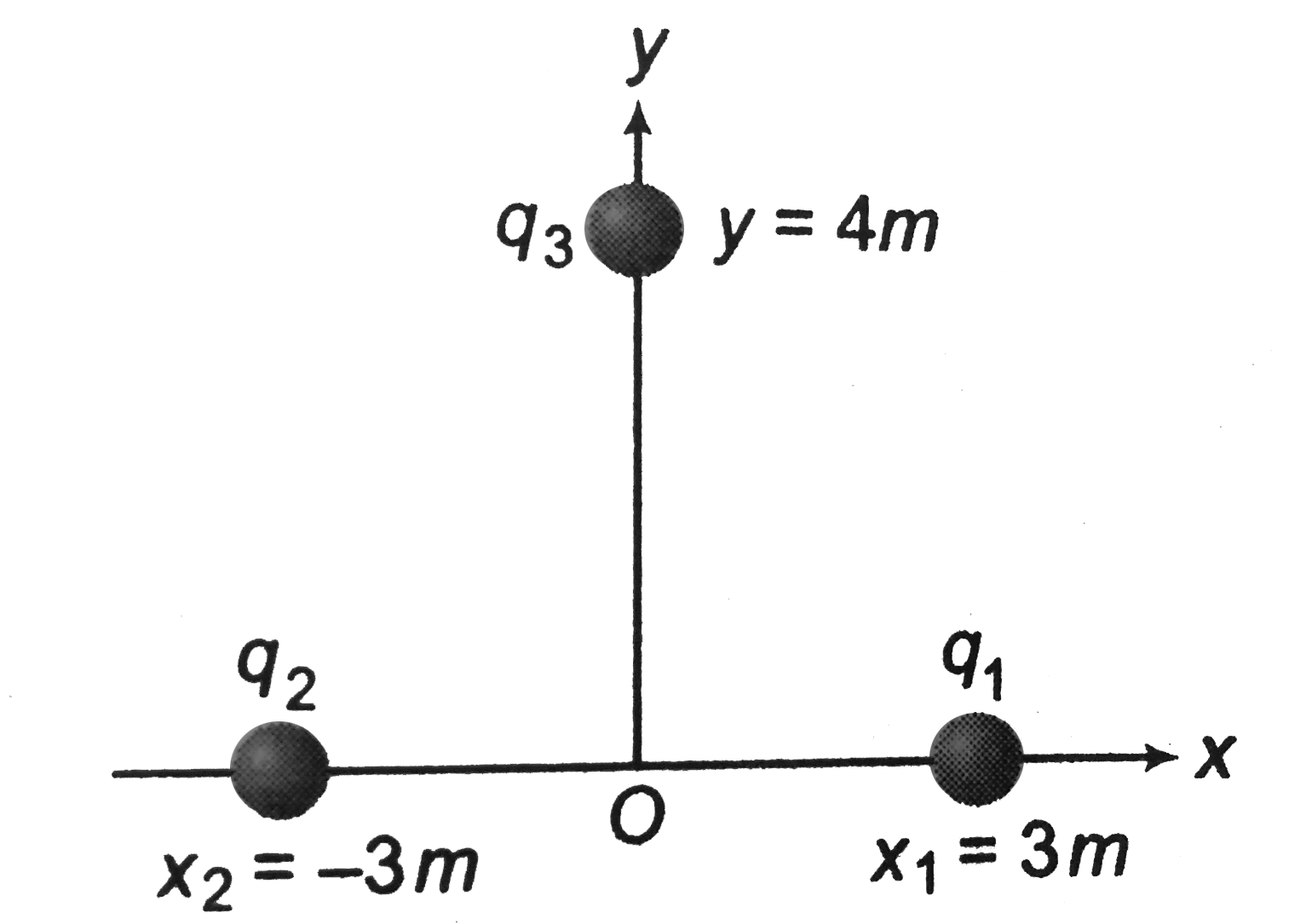 View Solution
View SolutionTwo point charges q1=q2=2μC are fixed at x1=+3m and x2=−3m as shown in figure. A third particle of mass 1 g and charge q3=−4μC are released from rest at y=4.0m.Find the speed of the particle as it reaches the origin.
 View Solution
View Solution

