The resultant of A and B is R1 On reversing the vector B , the resultant R2 what is the value of R21+R22?
A2+B2
A2−B2
2(A2+B2)
2(A2−B2)
The correct Answer is:C
Step by step video & image solution for The resultant of A and B is R_(1) On reversing the vector B , the resultant R_(2) what is the value of R_(1)^(2)+ R_(2)^(2)? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- BASIC MATHEMATICS & VECTORSBOOK - VMC MODULES ENGLISHCHAPTER - BASIC MATHEMATICS & VECTORSEXERCISE - Impeccable
50 Videos
- BASIC MATHEMATICS & VECTORSBOOK - VMC MODULES ENGLISHCHAPTER - BASIC MATHEMATICS & VECTORSEXERCISE - Enable
50 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 48
1 Videos
Similar Questions
The resultant vector of →P and →Q is →R. On reversing the direction of →Q the resultant vector becomes →S. Show that R2+S2=2(P2+Q2)
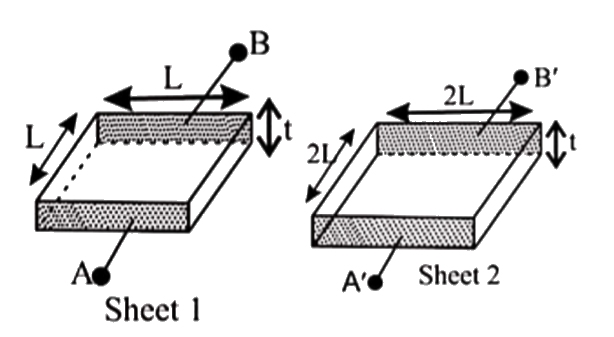
View SolutionThe resistance of metal sheet 1 between A and B is R1 and the resistance of sheet 2 between A' and B' is R2. The value of the ratio R1R2 is
View SolutionThe circuit is shown in the following figure. The potential at points A, B, C, D and O are given. The currents in the resistance R1,R2 and R3 are in the ratio of 4:2:1. What is the ratio of resistance R1,R2,R3 and R4 ?

View SolutionThe angle between two vector A and B is θ. Vector R is the resultant of the two vectors. If R makes an angle θ2 with A, then
View SolutionShow that 16R2rr1r2r3=a2b2c2
View SolutionA and B are two points on the parabola y2=4ax with vertex O. if OA is perpendicular to OB and they have lengths r1 and r2 respectively, then the valye of r4/31r4/32r2/31+r2/32 is
View SolutionIn an equilateral triangle with usual notations the value of 27r2Rr1r2r3is equal to
View SolutionIn ΔABC, if r=1,R=3,ands=5, then the value of a2+b2+c2 is _____
View SolutionIf r,r1,r2,r3 have their usual meanings , the value of 1r1+1r2+1r3, is
View SolutionThree circles with radius r1,r2,r3 touch one another externally. The tangents at their point of contact meet at a point whose distance from a point of contact is 2. The value of (r1r2r3r1+r2+r3) is equal to
View Solution
