The acceleratin of a particle increases linearly with time t as 6t. If the initial velocity of the particles is zero and the particle starts from the origin, then the distance traveled by the particle in time t will be
t
t2
t3
t4
The correct Answer is:C
To solve the problem step by step, we will follow the principles of kinematics, specifically focusing on the relationship between acceleration, velocity, and distance.
Step 1: Understand the given information
We are given that the acceleration a of the particle varies with time t as:
a=6t
The initial velocity u is zero, and the particle starts from the origin (initial position x0=0).
Step 2: Relate acceleration to velocity
Acceleration is defined as the rate of change of velocity with respect to time:
a=dvdt
Substituting the expression for acceleration:
dvdt=6t
Step 3: Integrate to find velocity
To find the velocity v, we integrate both sides with respect to time t:
∫dv=∫6tdt
This gives:
v=3t2+C
Since the initial velocity u=0 when t=0, we can determine the constant C:
0=3(0)2+C⟹C=0
Thus, the velocity function is:
v=3t2
Step 4: Relate velocity to distance
Velocity is also defined as the rate of change of distance with respect to time:
v=dxdt
Substituting the expression for velocity:
dxdt=3t2
Step 5: Integrate to find distance
To find the distance x, we integrate both sides with respect to time t:
∫dx=∫3t2dt
This gives:
x=t3+C′
Since the particle starts from the origin (initial position x0=0 when t=0), we can determine the constant C′:
0=(0)3+C′⟹C′=0
Thus, the distance function is:
x=t3
Step 6: Conclusion
The distance traveled by the particle in time t is:
t3
We are given that the acceleration a of the particle varies with time t as:
a=6t
The initial velocity u is zero, and the particle starts from the origin (initial position x0=0).
Acceleration is defined as the rate of change of velocity with respect to time:
a=dvdt
Substituting the expression for acceleration:
dvdt=6t
To find the velocity v, we integrate both sides with respect to time t:
∫dv=∫6tdt
This gives:
v=3t2+C
Since the initial velocity u=0 when t=0, we can determine the constant C:
0=3(0)2+C⟹C=0
Thus, the velocity function is:
v=3t2
Velocity is also defined as the rate of change of distance with respect to time:
v=dxdt
Substituting the expression for velocity:
dxdt=3t2
To find the distance x, we integrate both sides with respect to time t:
∫dx=∫3t2dt
This gives:
x=t3+C′
Since the particle starts from the origin (initial position x0=0 when t=0), we can determine the constant C′:
0=(0)3+C′⟹C′=0
Thus, the distance function is:
x=t3
The distance traveled by the particle in time t is:
t3
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE & PLANE BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - ENABLE
50 Videos
- MOTION IN A STRAIGHT LINE & PLANE BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - EFFICIENT
50 Videos
- MOCK TEST 9BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 9EXERCISE - PHYSICS (SECTION 2)
5 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-J
10 Videos
Similar Questions
The velocity of a particle is zero at t=0
View SolutionThe velocity of a particle is zero at time t = 2s, then
View SolutionThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v0. The distance travelled by the particle in time t will be
View SolutionThe acceleration of paticle varies with time as :
a(t)=3t2+4
If the initial velocity of particle is 2m/s, find the velocity of particle at t=3sec.
View SolutionThe acceleration of a particle which starts from rest varies with time according to relation a=2t+3. The velocity of the particle at time t would be
View SolutionThe acceleration of a'particle starting from rest, varies with time according to the relation a=kt+c. The velocity of the particle after time t will be :
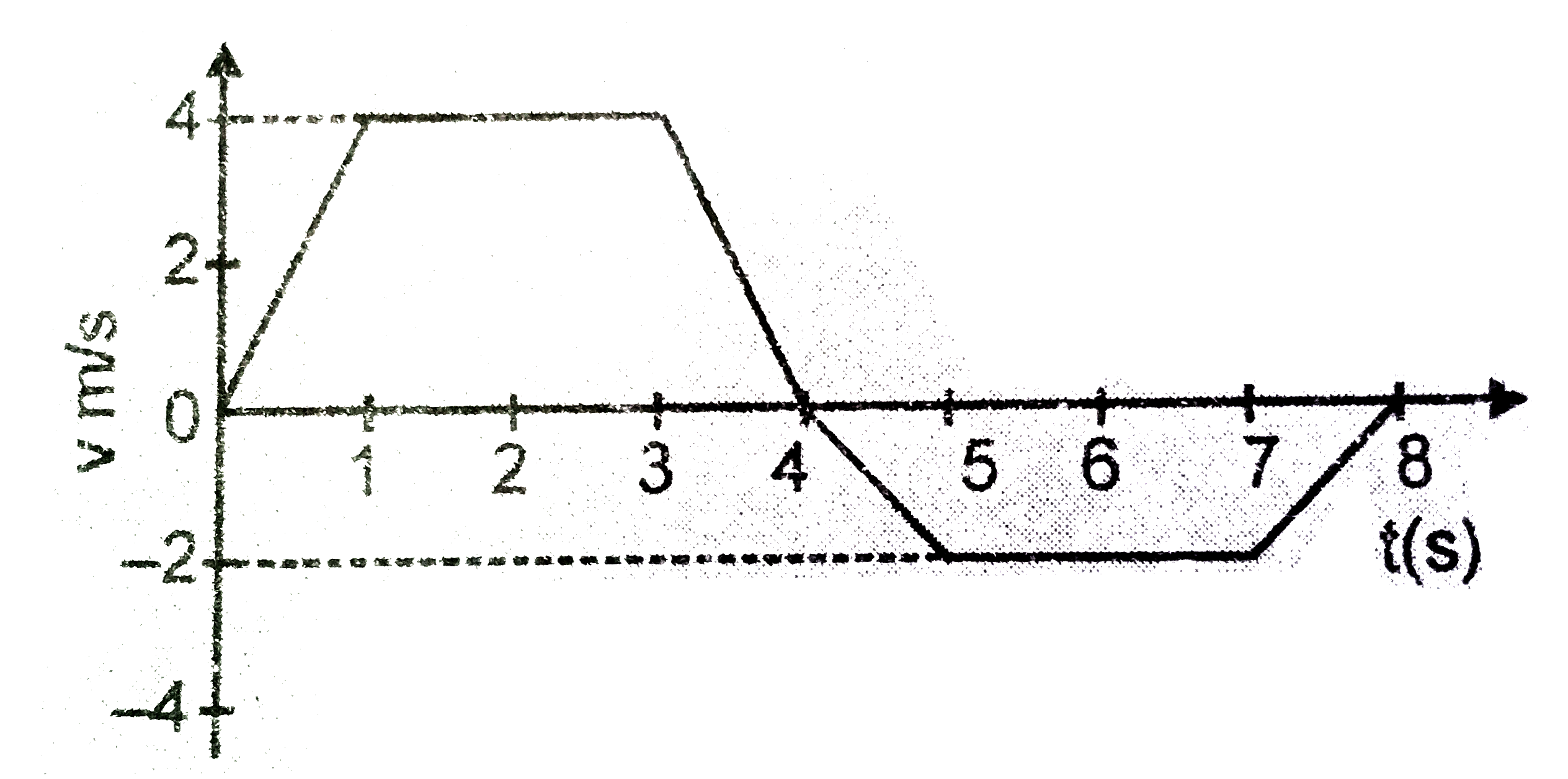
View SolutionA particle moves in a straight line from origin. Its velocity time curve is shown. Find the distance of particle at the =8sec. From the origin and the distance travelled by the particle during first 8 seconds.
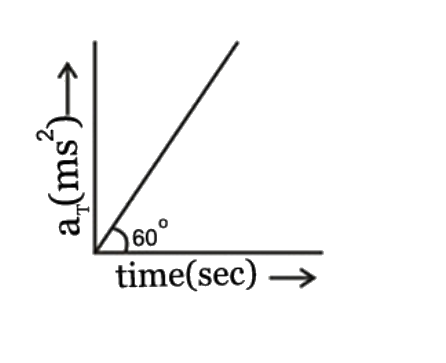
View SolutionTangental acceleration of a particle moving in a circle of radius 1 m varies with time t as shown in figure (initial velocity of the particle is zero). Time after which total acceleration of particle makes an angle of 30∘ with radial acceleration is
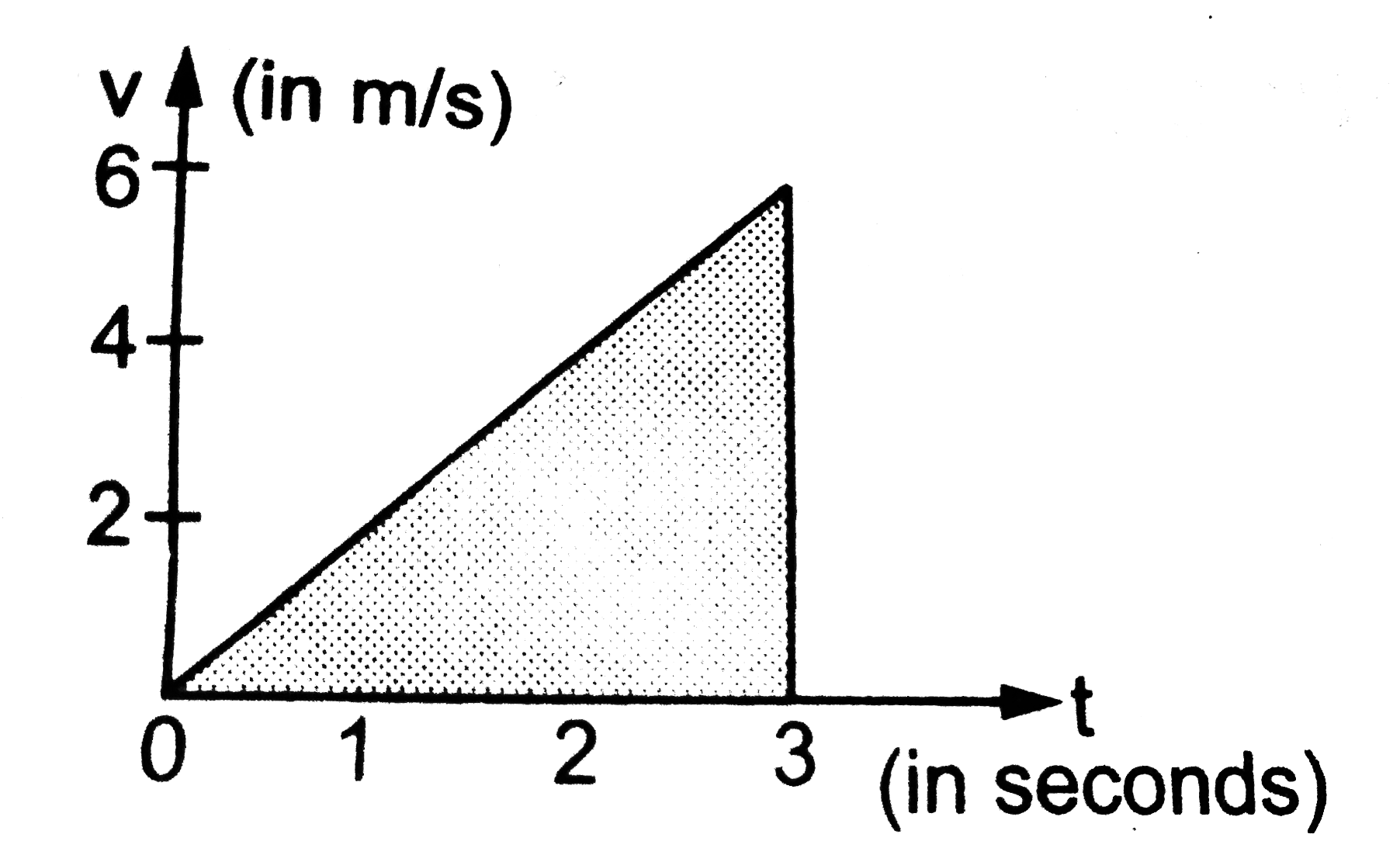
View SolutionFigure shows the speed versus time graph for a particle. Find the distance travelled by the particle during the time t=0 to t=3s.
View SolutionThe position of a particle along x-axis at time t is given by x=1+t−t2. The distance travelled by the particle in first 2 seconds is
View Solution
