Question

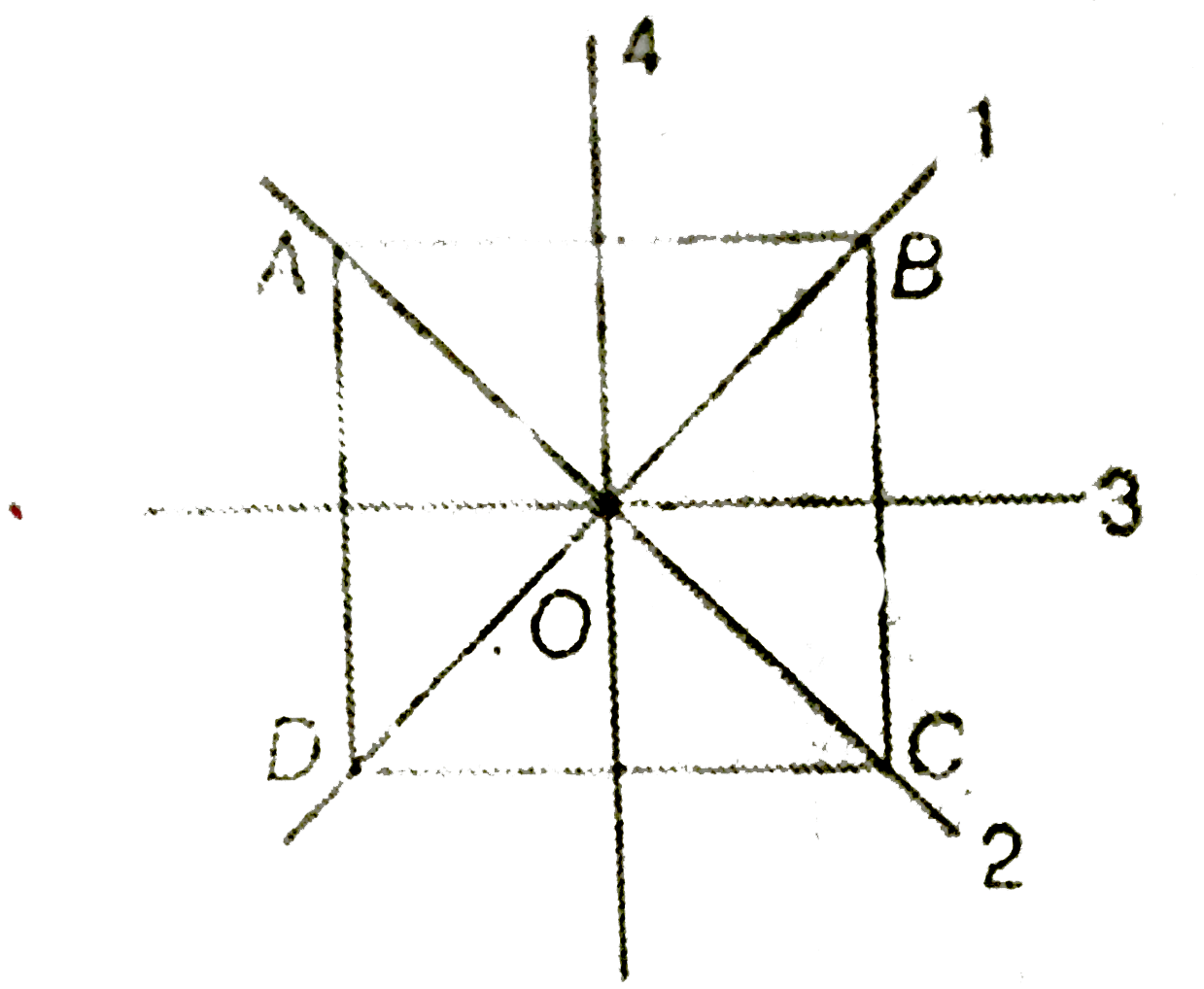
Four masses 1, 2, 3 and 4 kg each are placed on four corners A, B, C and D of a square of side $\sqrt{2}$ m. The moment of inertia of this system about an axis passing through the point of inter-section of diagonals and perpendicular to the plane of the square will be:

Options

A. `5kg m^(2)`
B. `7.5kgm^(2)`
C. `10kg m^(2)`
D. `12.5kg m^(2)`

Answer

C

Explanation

To find the moment of inertia of the system of four masses located at the corners of a square, we can follow these steps:

1. Identify the Masses and Their Positions:
- The four masses are placed at the corners of a square:
- Mass \( m_1 = 1 \, \text{kg} \) at corner A
- Mass \( m_2 = 2 \, \text{kg} \) at corner B
- Mass \( m_3 = 3 \, \text{kg} \) at corner C
- Mass \( m_4 = 4 \, \text{kg} \) at corner D
- The side length of the square is \( \sqrt{2} \, \text{m} \).

2. Calculate the Distance from the Center:
- The center of the square (point O) is the intersection of the diagonals.
- The distance from the center to any corner (e.g., A) can be calculated using the Pythagorean theorem.
- The distance \( OA \) can be calculated as:
\( OA = \frac{\text{side length}}{2} \sqrt{2} = \frac{\sqrt{2}}{2} \times \sqrt{2} = 1 \, \text{m} \)
- Therefore, \( OA = OB = OC = OD = 1 \, \text{m} \).

3. Apply the Moment of Inertia Formula:
- The moment of inertia \( I \) about an axis perpendicular to the plane of the square and passing through the center is given by:
\( I = m_1 r_1^2 + m_2 r_2^2 + m_3 r_3^2 + m_4 r_4^2 \)
- Substituting the values:
\( I = 1 \cdot (1^2) + 2 \cdot (1^2) + 3 \cdot (1^2) + 4 \cdot (1^2) \)
- This simplifies to:
\( I = 1 \cdot 1 + 2 \cdot 1 + 3 \cdot 1 + 4 \cdot 1 = 1 + 2 + 3 + 4 = 10 \, \text{kg m}^2 \)

4. Conclusion:
- The moment of inertia of the system about the given axis is \( 10 \, \text{kg m}^2 \).

Final Answer:
The moment of inertia of the system is \( I = 10 \, \text{kg m}^2 \).

---