A circular disc is rotating about an axis through its circumference in a vertical plane. If its mass is 0.1 kg and radius 0.5 m, its M.I. In kg. m2 units about this axis will be
(a)0.0375
(b)0.025
(c)0.5
(d)0.75
The correct Answer is:A
To find the moment of inertia (M.I.) of a circular disc rotating about an axis through its circumference, we can follow these steps:
Step 1: Understand the Moment of Inertia Formula
The moment of inertia of a solid disc about its center is given by the formula:
ICM=12MR2
where:
- ICM is the moment of inertia about the center of mass,
- M is the mass of the disc,
- R is the radius of the disc.
Step 2: Use the Parallel Axis Theorem
Since the disc is rotating about an axis through its circumference, we need to use the parallel axis theorem. The parallel axis theorem states:
I=ICM+Md2
where:
- d is the distance from the center of mass to the new axis of rotation. For a disc, this distance is equal to the radius R.
Step 3: Calculate ICM
Substituting the values of mass M=0.1kg and radius R=0.5m into the formula for ICM:
ICM=12(0.1)(0.5)2
ICM=12(0.1)(0.25)
ICM=12(0.025)
ICM=0.0125kg m2
Step 4: Calculate I using the Parallel Axis Theorem
Now, we apply the parallel axis theorem:
I=ICM+MR2
Substituting the values:
I=0.0125+(0.1)(0.5)2
I=0.0125+(0.1)(0.25)
I=0.0125+0.025
I=0.0375kg m2
Final Answer
Thus, the moment of inertia of the disc about the axis through its circumference is:
I=0.0375kg m2
The moment of inertia of a solid disc about its center is given by the formula:
ICM=12MR2
where:
- ICM is the moment of inertia about the center of mass,
- M is the mass of the disc,
- R is the radius of the disc.
Since the disc is rotating about an axis through its circumference, we need to use the parallel axis theorem. The parallel axis theorem states:
I=ICM+Md2
where:
- d is the distance from the center of mass to the new axis of rotation. For a disc, this distance is equal to the radius R.
Substituting the values of mass M=0.1kg and radius R=0.5m into the formula for ICM:
ICM=12(0.1)(0.5)2
ICM=12(0.1)(0.25)
ICM=12(0.025)
ICM=0.0125kg m2
Now, we apply the parallel axis theorem:
I=ICM+MR2
Substituting the values:
I=0.0125+(0.1)(0.5)2
I=0.0125+(0.1)(0.25)
I=0.0125+0.025
I=0.0375kg m2
Thus, the moment of inertia of the disc about the axis through its circumference is:
I=0.0375kg m2
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - ENABLE
50 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EFFICIENT
50 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B
10 Videos
Similar Questions
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionA circular disc has a mass of 1kg and radius 40 cm. It is rotating about an axis passing through its centre and perpendicular to its plane with a speed of 10rev/s. The work done in joules in stopping it would be-
View SolutionA solid sphere of radius r and mass m rotates about an axis passing through its centre with angular velocity ω. Its K.E. Is
View SolutionOut of a disc of mass M and radius R a concentric disc of mass m and radius r is removed. The M.I. of the remaining part about the symmetric axis will be :
View SolutionIf a circular concentric hole is made on a disc then about an axis passing through the centre of the disc and perpendicular to its plane
View SolutionThe M.I of a uniform thin circular ring about an axis through its centre and normal to the plane of ring is I. Its M.I about a tangent in its plane is equal to
View SolutionFour similar point masses (each of mass m) are placed on the circumference of a disc of mass M and radius R. The M.I. of the system about the normal axis through the centre O will be:
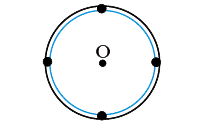
View SolutionA disc is rotating about vertical axis OA, which is tangent to the circumference and perpendicular to the plane of disc. Its rotational energy is given as E. Find the time period of rotation.

View SolutionA sphere of mass 10 kg and radius 0.5 m rotates about a tangent. The moment of inertia of the sphere is
View SolutionThe M.I. of a thin ring of mass M and radius R about an axis through the diameter in its plane will be:
View Solution
