A stone attached to one end of string is revolved around a stick so that the string winds upon the stick and gets shortened. What is conserved ?
angular momentum
linear momentum
kinetic energy
none of the above
The correct Answer is:A
To solve the problem of a stone attached to a string being revolved around a stick while the string winds upon the stick and gets shortened, we need to analyze the motion and the quantities involved.
1. Understanding the System:
- We have a stone attached to a string that is being revolved around a stick. As the stone moves in a circular path, the string winds around the stick, effectively shortening the radius of the circular motion.
2. Identifying Key Concepts:
- The stone undergoes circular motion, and as the radius decreases (due to the string winding up), the angular velocity of the stone will change.
- We need to determine what physical quantity remains constant during this process.
3. Angular Momentum:
- Angular momentum (L) for a point mass moving in a circular path is given by the formula:
L=m⋅v⋅r
- Where m is the mass of the stone, v is its linear velocity, and r is the radius of the circular path.
4. Relation Between Linear Velocity and Angular Velocity:
- The relationship between linear velocity (v), angular velocity (ω), and radius (r) is given by:
v=ω⋅r
- Thus, we can express angular momentum in terms of angular velocity:
L=m⋅(ω⋅r)⋅r=m⋅ω⋅r2
5. Conservation of Angular Momentum:
- As the radius r decreases (the string winds up), the angular velocity ω must increase to keep the angular momentum L constant (conserved).
- This is due to the conservation of angular momentum, which states that if no external torque acts on a system, the total angular momentum remains constant.
6. Conclusion:
- Therefore, the quantity that is conserved in this scenario is the angular momentum of the stone as it revolves around the stick.
Final Answer:
The conserved quantity is angular momentum.
- We have a stone attached to a string that is being revolved around a stick. As the stone moves in a circular path, the string winds around the stick, effectively shortening the radius of the circular motion.
- The stone undergoes circular motion, and as the radius decreases (due to the string winding up), the angular velocity of the stone will change.
- We need to determine what physical quantity remains constant during this process.
- Angular momentum (L) for a point mass moving in a circular path is given by the formula:
L=m⋅v⋅r
- Where m is the mass of the stone, v is its linear velocity, and r is the radius of the circular path.
- The relationship between linear velocity (v), angular velocity (ω), and radius (r) is given by:
v=ω⋅r
- Thus, we can express angular momentum in terms of angular velocity:
L=m⋅(ω⋅r)⋅r=m⋅ω⋅r2
- As the radius r decreases (the string winds up), the angular velocity ω must increase to keep the angular momentum L constant (conserved).
- This is due to the conservation of angular momentum, which states that if no external torque acts on a system, the total angular momentum remains constant.
- Therefore, the quantity that is conserved in this scenario is the angular momentum of the stone as it revolves around the stick.
The conserved quantity is angular momentum.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE
56 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - ENABLE
50 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B
10 Videos
Similar Questions
A particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl

The maximum angle made by the string with downward vertical is
View SolutionAt stone is tied to the end of a string and is whirled in a horizontal aide with a constant speed. Suppose the string breaks suddenly. What happens to the stone ?
View SolutionA stone tied to the end of a string is whirled in a horizontal circle. The mass of the stone is 1.0 kg and the string is 0.50 m long. If the stone revolves at a constant speed for 10 times in 15.71 s, (a) what is the tension in the string? (b) What would happen to the tension in the string if the mass was doubled and all the other quantities remained the same? (c) What would happen to the tension in the string if the period was doubled and all the other quantities remain the same?
View SolutionA string 1 m long can just support a weight of 16 kg. Amass of 1 kg is attached to one of its ends. The body is revolved in a horizontal circle about the other fixed end of the string. Find the greatest number of revolutions made by the mass per second ? (Take g = 10ms−2)
View SolutionA particle of mass 200g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g=10ms2)
View SolutionA string 1 m long can just support a weight of 16 kg. A mass of 1 kg is attached to one of its ends. The body is revolved in a horizontal circle about the other fixed end of the stringy Find the greatest number of revolutions made by the mass per seconds ? (Take g=10ms−2)
The maximum tension the string can withstand = weight of 16 kg.
View SolutionA stone is attached to one end of a string and rotated in verticle cricle .If string breaks at the position of maximum tension, will break at
View SolutionA stone is fastened to one end of a string and is whirled in a verticla circle of radius R. Find the minimum speed the stone can have at the highest point of the circle.
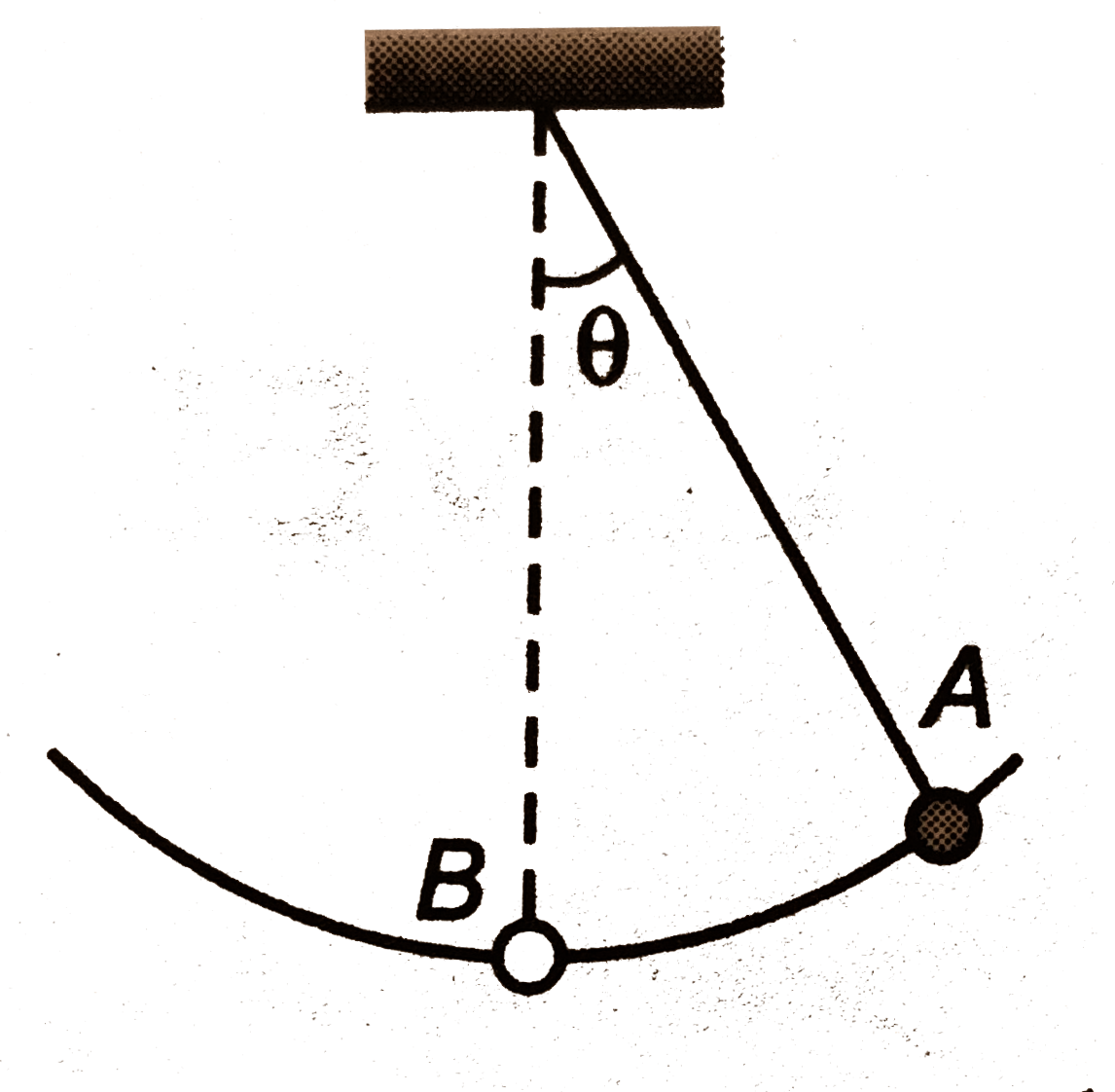
View SolutionA ball attached to one end of a string swings in a vertical plane such that its acceleration at point A (extreme position) is equal to its acceleration at point B (mean position), The angle θ is
View SolutionA string passing over a smooth pulley carries a stone at one end, while its other end is attached to a vibrating tuning fork and the string vibrates forming 8 loops. When the stone is immersed in water 10 loops are formed. The specific gravity of the stone is
View Solution
