A set of 4 cell each of emf 2V and internal resistance 1.5Ω are connected across an external load of 10Ω with 2 rows, two cells in each row. Calculate the current in each row and potential difference across 10Ω
The correct Answer is:(3.5V)
To solve the problem, we need to analyze the circuit configuration and calculate the current in each row of cells and the potential difference across the external load of 10Ω.
Step 1: Understand the Circuit Configuration
We have 4 cells, each with an EMF of 2V and an internal resistance of 1.5Ω. The cells are arranged in two rows, with two cells in series in each row. The two rows are then connected in parallel across a 10Ω external load.
Step 2: Calculate the Equivalent EMF and Internal Resistance for Each Row
Since the two cells in each row are in series, the equivalent EMF (E_eq) for each row is:
Eeq=E1+E2=2V+2V=4V
The internal resistance (R_eq) for two cells in series is:
Req=R1+R2=1.5Ω+1.5Ω=3Ω
Thus, each row can be represented as a single battery of 4V and 3Ω.
Step 3: Calculate the Total Resistance in the Circuit
Now, we have two rows of batteries (each with 4V and 3Ω) connected in parallel with the external load of 10Ω. The total internal resistance of the two rows in parallel is given by:
Rtotal=Req1×Req2Req1+Req2=3Ω×3Ω3Ω+3Ω=9Ω6Ω=1.5Ω
Step 4: Calculate the Total EMF in the Circuit
Since both rows have the same EMF, the total EMF in the circuit remains:
Etotal=4V
Step 5: Calculate the Total Resistance in the Circuit
The total resistance in the circuit is the sum of the equivalent internal resistance and the external load:
Rtotal=Rinternal+Rexternal=1.5Ω+10Ω=11.5Ω
Step 6: Calculate the Total Current in the Circuit
Using Ohm's law, the total current (I) in the circuit can be calculated as:
I=EtotalRtotal=4V11.5Ω≈0.3478A
Step 7: Calculate the Current in Each Row
Since the two rows are in parallel, the current splits equally between them. Therefore, the current in each row (I_row) is:
Irow=I2=0.3478A2≈0.1739A
Step 8: Calculate the Potential Difference Across the External Load
The potential difference (V_load) across the external load can be calculated using Ohm's law:
Vload=I×Rexternal=0.3478A×10Ω≈3.478V
Final Answers
- Current in each row: ≈0.1739A
- Potential difference across the 10Ω load: ≈3.478V
We have 4 cells, each with an EMF of 2V and an internal resistance of 1.5Ω. The cells are arranged in two rows, with two cells in series in each row. The two rows are then connected in parallel across a 10Ω external load.
Since the two cells in each row are in series, the equivalent EMF (E_eq) for each row is:
Eeq=E1+E2=2V+2V=4V
The internal resistance (R_eq) for two cells in series is:
Req=R1+R2=1.5Ω+1.5Ω=3Ω
Thus, each row can be represented as a single battery of 4V and 3Ω.
Now, we have two rows of batteries (each with 4V and 3Ω) connected in parallel with the external load of 10Ω. The total internal resistance of the two rows in parallel is given by:
Rtotal=Req1×Req2Req1+Req2=3Ω×3Ω3Ω+3Ω=9Ω6Ω=1.5Ω
Since both rows have the same EMF, the total EMF in the circuit remains:
Etotal=4V
The total resistance in the circuit is the sum of the equivalent internal resistance and the external load:
Rtotal=Rinternal+Rexternal=1.5Ω+10Ω=11.5Ω
Using Ohm's law, the total current (I) in the circuit can be calculated as:
I=EtotalRtotal=4V11.5Ω≈0.3478A
Since the two rows are in parallel, the current splits equally between them. Therefore, the current in each row (I_row) is:
Irow=I2=0.3478A2≈0.1739A
The potential difference (V_load) across the external load can be calculated using Ohm's law:
Vload=I×Rexternal=0.3478A×10Ω≈3.478V
- Current in each row: ≈0.1739A
- Potential difference across the 10Ω load: ≈3.478V
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE EXERCISE-6
5 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-A
10 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - PRACTICE EXERCISE-3
4 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 48
1 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE
68 Videos
Similar Questions
Three identical cells, each of emf 2 V and internal resistance 0.2Ω are connected in series to an external resistor of 7.4Ω. Calculate the current in the circuit.
View Solution24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View SolutionA cell whose e.m.f. is 2V and internal resistance is 0.1Ω is connected with a resistance of 3.9Ω the voltage across the cell terminal will be
View SolutionA cell of e.m.f. 2 V and internal resistance 1.2 Ω is connected to an ammeter of resistance 0.8 Ω and two resistors of 4.5 Ω and 9 Ω as shown in Fig.
find : the potential difference across the 4.5 Ω resistor.
View SolutionFind the current drawn from a cell of emf 2 V and internal resistance 2Ω connected to the network given below.
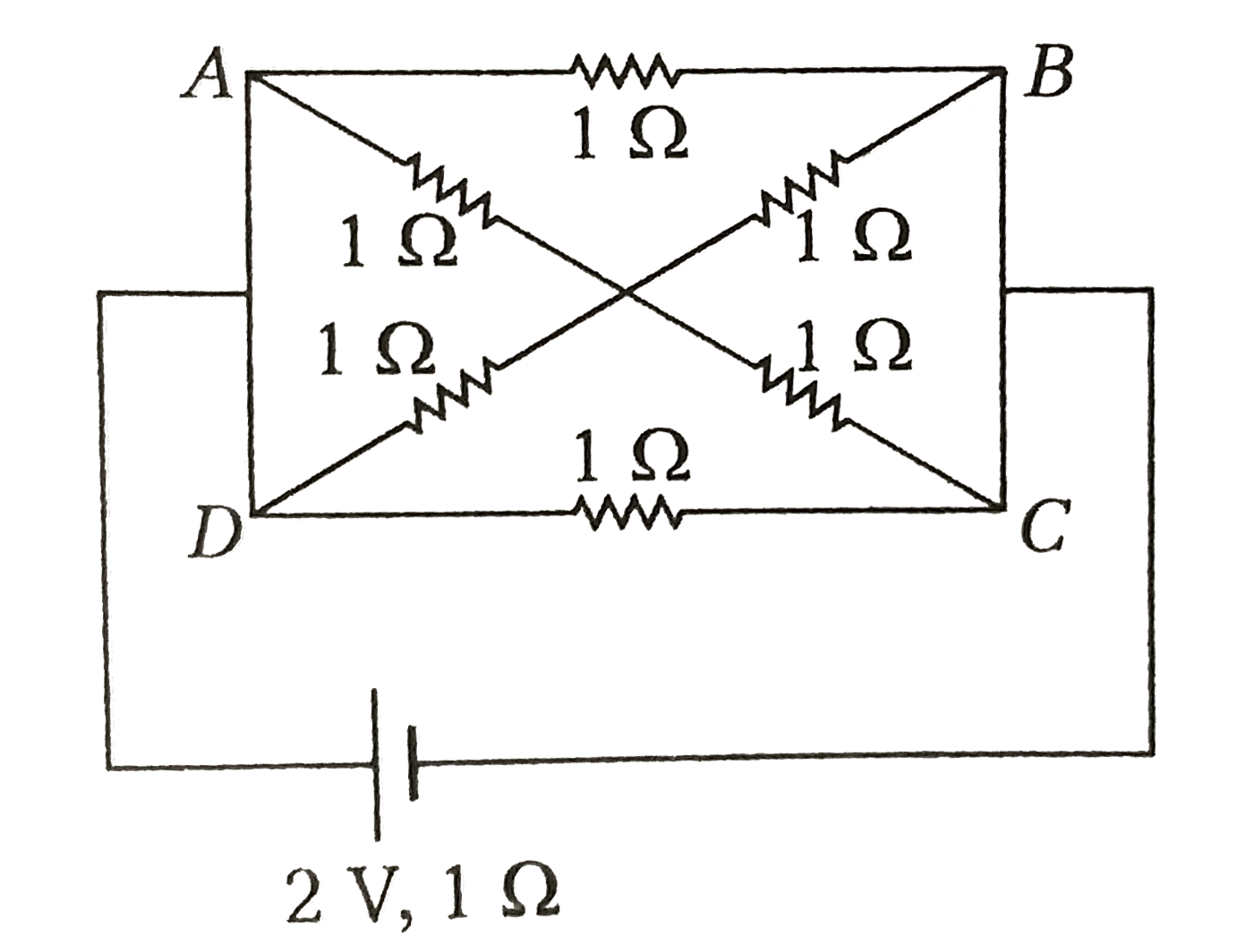
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
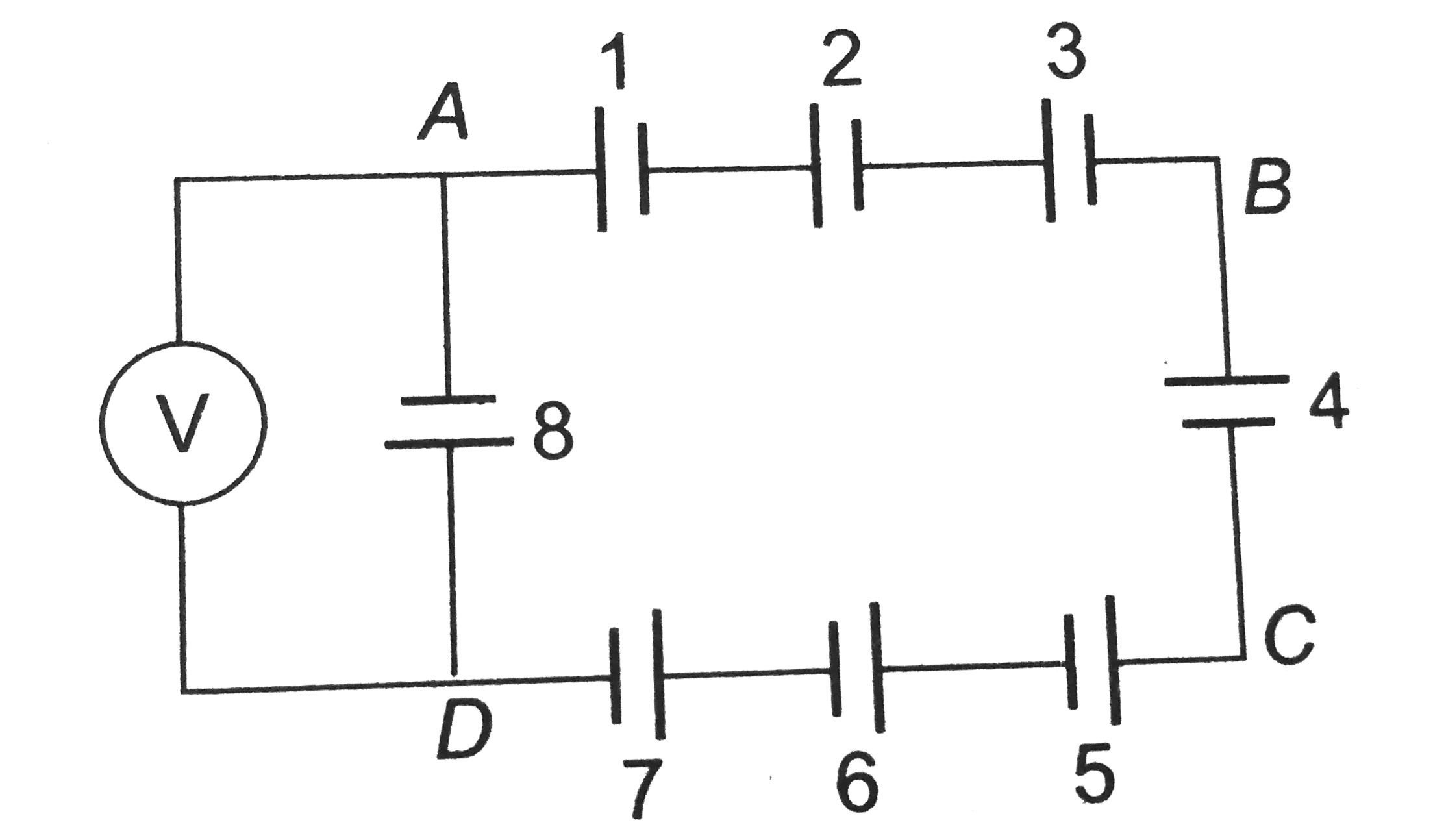
View SolutionEight cells marked 1 to 8, each of emf 5V and internal resistance 0.2Ω are connected as shown. What is the reading of ideal voltmeter ?
View SolutionA cell of e.m.f. 1.5 V, internal resistance 1 Ω is connected to the resistors of 4 Ω and 20Ω in series. Draw a circuit diagram and calculate :
the current in the circuit,
View SolutionA cell of e.m.f. 2V and internal resistance 1.2.Ω is connected with an ammeter of resistance 0.8Ω and two resistors of 4.5 Ω and 9Ω as shown in the diagram below:
What is the potential difference across the terminals of the cell?
View SolutionIn the circuit diagram given below, a cell of 9 V and internal resistance of 0.5(Ω) is connected across a resistor A of 2Ω in series and two resistors of 2Ω and 6Ω in parallel.
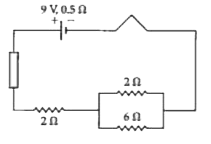
Find
The potential difference across the terminals of the cell.
View Solution
