Derive an expression for the potential at a distance r from a point charge +q.
Potential due to a point charge Let P be the point at a distance r from the origin O at which the electric potential due to charge +q is required
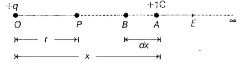
The electric potential at a point P is the amount of work done in carrying a unit positive charge from ∞ to P. As work done is independent of the path, we choose a convenient path along the radial direction from infinity to the point P without acceleration. Let A be an intermediate point on this path, where OA= x. The electrostatic force on unit positive charge at A is F=14πε0qx2, (along OA)...(i)
Small work done in moving the charge through a distance dx from A to B,
dW=Fdx=Fdxcos180∘=−Fdx[∵cos180∘=−1]dW=−Fdx ....(ii)
Total work done in moving unit positive charge from ∞ to the point P is
W=∫r∞−Fdx=∫r∞−14πε0.qx2dx
=−q4πε0∫r∞x−3dx=−q4πε0[−1x]r∞[∵∫x−2dx=−1x]
=q4πε0[1r−1∞]
⇒W=q4πε0 ...(iii)
From the definition of electric potential, this work is equal to the potential at point P,
V=q4πε0r ...(iv)
A positively charged particle produces a positive electric potential. A negatively charged particle produces a negative electric potential.
Similar Questions
Find an expression for the potential at a point due to a point charge Q.
View SolutionExplain the conept of electric potential energy.
Derive an expression for potential energy of a system of two point charges. Generalise the expression fo N discrete charges.
View Solution(a) Write two properties by which electric potential is related to the electric field .
(b) Two point charges q1andq2 separated by a distance of r12 are kept in air. Derive an expression for the potential energy of the system of two charges .
View SolutionDerive an expression for the electric potential at any point P at a distance r from the center of an electric dipole, making angle α with its axis.
View SolutionA thin circular ring of radius r is charged uniformly so that its linear charge density becomes λ . Derive an expression for the electric field at a point P at a distance x from it along the axis of the ring. Hence, prove that at large distances (r >> r), the ring behaves as a point charge.
View SolutionObtain an expression for electric potential .V due to a point charge .Q at a distance r.
View SolutionShow that electric potential at a point P, at a distance .r. from a fixed point charge Q, is given by :
V=(14πε0)Qr
View Solution(a) Obtain the expression for the potential due to a point charge.
(b) Use the above expression to show that the potential, due to an electric dipole (length 2a), varies as the inverse square' of the distance r of the 'field point' from the centre of the dipole for r>a.
View Solution(a) Obtain the expression for the potential due to a point charge.
(b) Use the above expression to show that the potential, due to an electric dipole (length 2a), varies as the inverse square' of the distance r of the 'field point' from the centre of the dipole for r>a.
View SolutionA charge Q is distributed over the surfaces of two concentric hollow spheres of radii r and R(R>>r) , such that their surface charge densities are equal . Derive the expression for the potential at the common centre.
View Solution
