A boy is pushing a box on horizontal floor from a position of rest to rest , while moving along a straight line. Consider the three phases of motion. The floor is rough with a small friction coefficient .
(i) Initially a constant hard push on the box to get it moving and attain a maximum velocity .
(ii) Mild push to keep the box moving with constant velocity
(iii) To pull back the box the to bring it to stop with the same retardation.
Which of the following graph is CORRECT ?
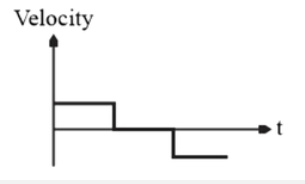
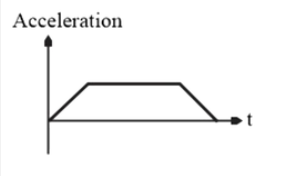
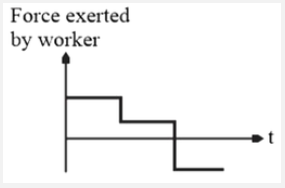
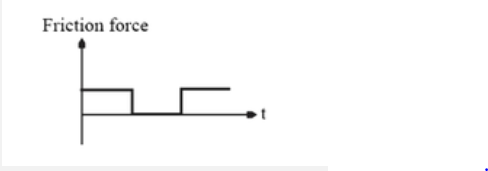
The correct Answer is:C
To solve the problem, we need to analyze the three phases of motion of the box and how the forces acting on it change during each phase. We will also consider the relationship between force, acceleration, and velocity.
1. Phase 1: Initial Hard Push
- The boy applies a constant hard push (F1) on the box to get it moving.
- The box experiences a frictional force (F_R) opposing the motion.
- The net force acting on the box can be expressed as:
Fnet1=F1−FR=m⋅a1
- Since the box starts from rest and accelerates, the acceleration (a1) is positive.
2. Phase 2: Mild Push to Maintain Constant Velocity
- In this phase, the boy applies a mild push (F2) to keep the box moving at a constant velocity.
- Since the velocity is constant, the acceleration is zero (a = 0).
- Therefore, the net force acting on the box is:
Fnet2=F2−FR=0
- This implies that the applied force (F2) is equal to the frictional force (F_R):
F2=FR
3. Phase 3: Pulling Back to Stop the Box
- The boy now applies a force (F3) in the opposite direction to bring the box to a stop with the same retardation.
- The frictional force (F_R) still opposes the motion.
- The net force during this phase can be expressed as:
Fnet3=F3−FR=−m⋅a2
- Here, the acceleration (a2) is negative (retardation), indicating that the box is slowing down.
4. Comparing Forces
- From the first phase, we know that F1>FR (since it causes acceleration).
- From the second phase, F2=FR.
- From the third phase, F3<FR (since it must overcome friction to decelerate the box).
5. Graph Representation
- The graph representing the forces should show:
- A high value for F1 during the initial push,
- A lower value for F2 during constant velocity,
- An even lower value for F3 during the deceleration phase.
- The acceleration should be positive during the first phase, zero during the second phase, and negative during the third phase.
Conclusion:
The correct graph will show:
- A peak for F1,
- A plateau for F2,
- A drop for F3,
- Corresponding changes in acceleration (positive, zero, negative).
- The boy applies a constant hard push (F1) on the box to get it moving.
- The box experiences a frictional force (F_R) opposing the motion.
- The net force acting on the box can be expressed as:
Fnet1=F1−FR=m⋅a1
- Since the box starts from rest and accelerates, the acceleration (a1) is positive.
- In this phase, the boy applies a mild push (F2) to keep the box moving at a constant velocity.
- Since the velocity is constant, the acceleration is zero (a = 0).
- Therefore, the net force acting on the box is:
Fnet2=F2−FR=0
- This implies that the applied force (F2) is equal to the frictional force (F_R):
F2=FR
- The boy now applies a force (F3) in the opposite direction to bring the box to a stop with the same retardation.
- The frictional force (F_R) still opposes the motion.
- The net force during this phase can be expressed as:
Fnet3=F3−FR=−m⋅a2
- Here, the acceleration (a2) is negative (retardation), indicating that the box is slowing down.
- From the first phase, we know that F1>FR (since it causes acceleration).
- From the second phase, F2=FR.
- From the third phase, F3<FR (since it must overcome friction to decelerate the box).
- The graph representing the forces should show:
- A high value for F1 during the initial push,
- A lower value for F2 during constant velocity,
- An even lower value for F3 during the deceleration phase.
- The acceleration should be positive during the first phase, zero during the second phase, and negative during the third phase.
The correct graph will show:
- A peak for F1,
- A plateau for F2,
- A drop for F3,
- Corresponding changes in acceleration (positive, zero, negative).
Similar Questions
A body is imparted motion from rest to move in a straight line. If it is then obstructed by an opposite force, then
View SolutionA particle moves along a straight line path. After some time it comes to rest. The motion is with constant acceleration whose direction with respect to the direction of velocity is :
View Solution
Knowledge Check
A 20 kg block is initially at rest. A 75 N force is required to set the block in motion. After the motion a force of 60 N is applied to keep the block moving with constant speed. The coefficient of static friction is
A0.6B0.52C0.44D0.35
A particle moves along a straight line path. After some time it comes to rest. The motion is with constant acceleration whose direction with respect to the direction of velocity is :
View SolutionA particle starting from rest moves along a straight line with constant acceleration for this velocity displacement graph will have the form-
View SolutionA boy of mass M is applying a horizontal force to slide a box of mass M on a rough horizontal surface. The the floor is μ and the between the box and the floor is μ'. In which of the following cases it is certainly not possible to slide the box?
View SolutionA man pulls a box on a horizontal floor through a distance of 20 m with a force of 30 N applied along a rope tied to the box and making and angle of 60° with the horizontal. Calculate the work done.
View SolutionA lift is moving downwards with an acceleration equal to g. A block of mass m , kept on the floor of the lift of friction coefficient μ , is pulled horizontally . The friction acting on the block is
View SolutionA body starting from rest moves along a straight line with a constant acceleration. The variation of speed (v) with distance (s) is represented by the graph:
View SolutionA20 kg block is initally at rest. A 75 N force is required to set the block in motion. After the motion starts, a force of 60 N is required to keep the block moving with constant speed. The coefficient of static friction is
View Solution
