Let f(x)=x+2|x+1|+x−1∣.Iff(x)=k has exactly one real solution, then the value of k is 3 (b) 0 (c) 1 (d) 2Solution in Tamil
Let f(x)=x+2|x+1|+2|x−1|
y=f(x) changes definition at x=−1andx=1.
Since the graph of the function is a straight line in each region (−∞,−1),(−1,1)and(1,∞), we need to check the values at some particular values of x to draw the graphs.
f(−2)=−2+2(1)+2(3)=6
f(−1)=−1+2(0)+2(2)=3
f(1)=1+2(2)+2(0)=5
f(2)=2+2(3)+2(1)=10
Thus, we plot the points (−2,6),(−1,3),(1,5)and(2,10).
Plotting these points and connecting with the straight line, we have the following graph.
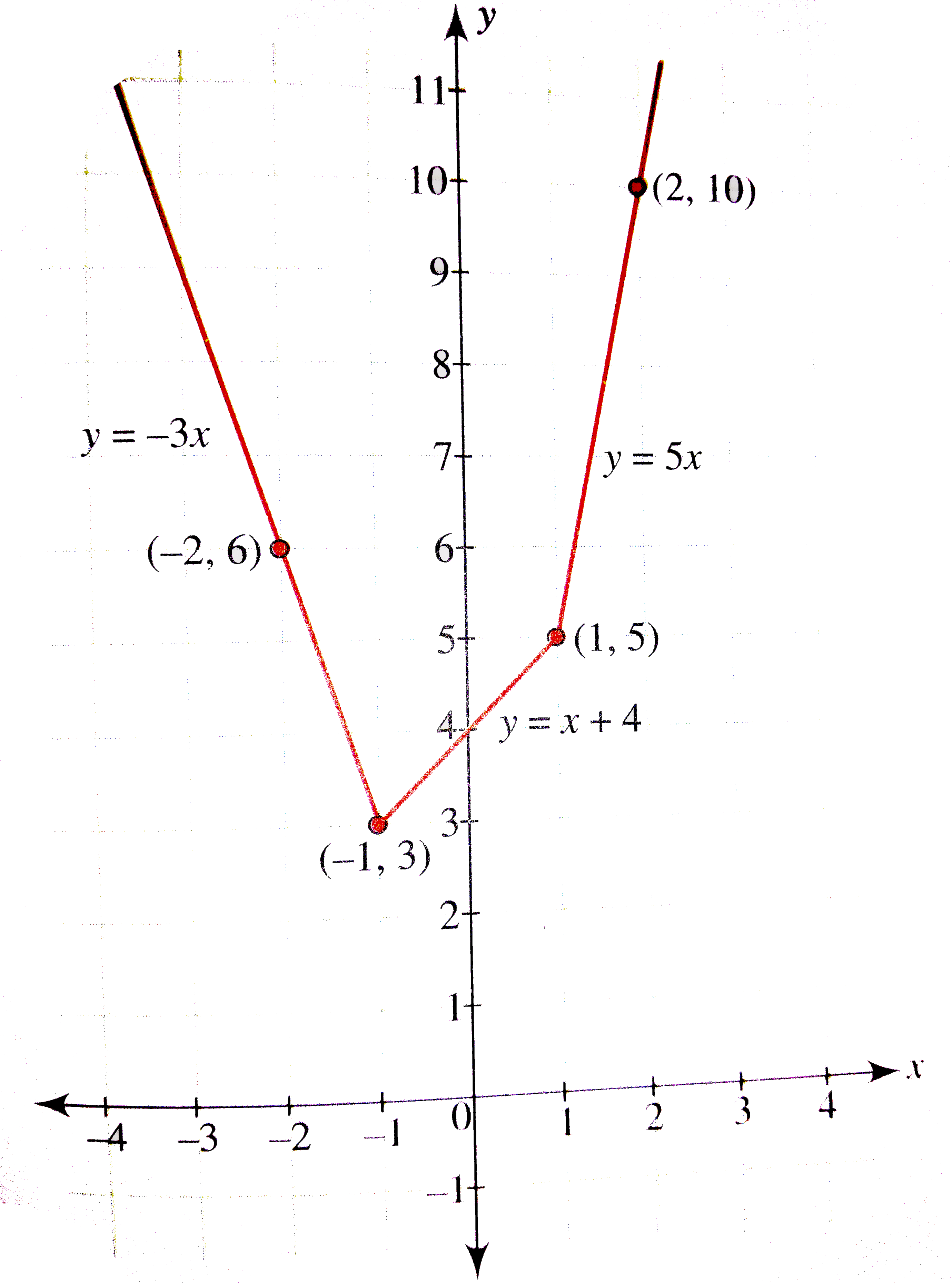
For the equation f(x)=k to have exactly one real root, the line y =k must intersect the graph of y=f(x) at the point (−1,3), hence the value of k is 3.
For the equation f(x)=k to have two negative real roots, the line y=k must intersect the graph of y=f(x) at the point between y=3andy=4, hence the values of k are (3,4).
For the equation f(x)=k to have real roots of opposite sign, the line y=k must intersect the graph of y=f(x) above y=4, hence the values of k are (4,∞).
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises4videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
Similar Questions
Draw the graph of y=1(1/x).
09:11View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=005:57View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
04:47View SolutionLet n_k be the number of real solutions |x+1|+|x-3|=K , then (a) n_K = 0 if K lt 4 (b) n_K = 2 if K gt 4 (c) n_K is infinitely many if K = 4 (d) Minimum value of f(x) = |x+1|+|x-3| is 2
05:18View SolutionIf x is real and k=x2−x+1x2+x+1 , then k∈[1/3,3] (b) k≥3 (c) k≤1/3 (d) none of these
02:09View SolutionLet f(x)=x+2|x+1|+2|x−1|. If f(x)=k has exactly one real solution, then the value of k is (a)3 (b) 0 (c)1 (d) 2
05:44View SolutionIf x is real and k=(x^(2)-x+1)/(x^(2)+x+1) then: (A) (1)/(3)<=k<=3(B)k<=5(C)k<=0(D) none
03:05View SolutionNumber of real values of k for which the equation x+2kx−1=x has exactly one real solution is (A) 0 (B) 1 (C) 2 (D) 3
08:14View SolutionIf |x−1|+|x−2|+|x−3|=k,xεR then value of k for which given equation has exactly one solution.
03:35View SolutionLet f(x)=x+2|x+1|+2|x−1|. Find the values of k if f(x)=k
(i) has exactly one real solution,
(ii) has two negative solutions,
(iii) has two solutions of opposite sign.06:54View SolutionLet f(x)=2|x|−1x−3
Range of the values of 'k' for which f(x)=k has exactly two distinct solutions:05:48View SolutionLet f(x)=x+2|x+1|+2|x−1|. If f(x)=k has exactly one real solution, then the value of k is (a)3 (b) 0 (c)1 (d) 2
07:40View SolutionLet f(x)=x+2|x+1|+2|x−1|. Find the values of k if f(x)=k
(i) has exactly one real solution,
(ii) has two negative solutions,
(iii) has two solutions of opposite sign.03:41View SolutionLet f(x)=x+2|x+1|+x−1∣.Iff(x)=k has exactly one real solution, then the value of k is 3 (b) 0 (c) 1 (d) 2
05:22View SolutionLet f(x)=2|x|−1x−3
Range of the values of 'k' for which f(x)=k has exactly two distinct solutions:04:59View SolutionLet f(x)=2|x|−1x−3
Range of the values of 'k' for which f(x)=k has exactly two distinct solutions:05:32View Solution

