Consider the area $S_{0}, S_{1}, S_{2} \dots .$ bounded by the x-axis and half-waves of the curve $y = e^{- x} \sin x, where x \geq 0 .$
The value of $S_{0}$ is Solution in Tamil

A

$\frac{1}{2} (1 + e^{π})$ sq. units

B

$\frac{1}{2} (1 + e^{- π})$ sq. units

C

$\frac{1}{2} (1 - e^{- π})$ sq. units

D

$\frac{1}{2} (e^{π} - 1)$ sq. units

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$Since - 1 \leq \sin x \leq 1, the curve y = e^{- x} \sin x is bounded by the curve y = e^{- x} and y = e^{- x} .$

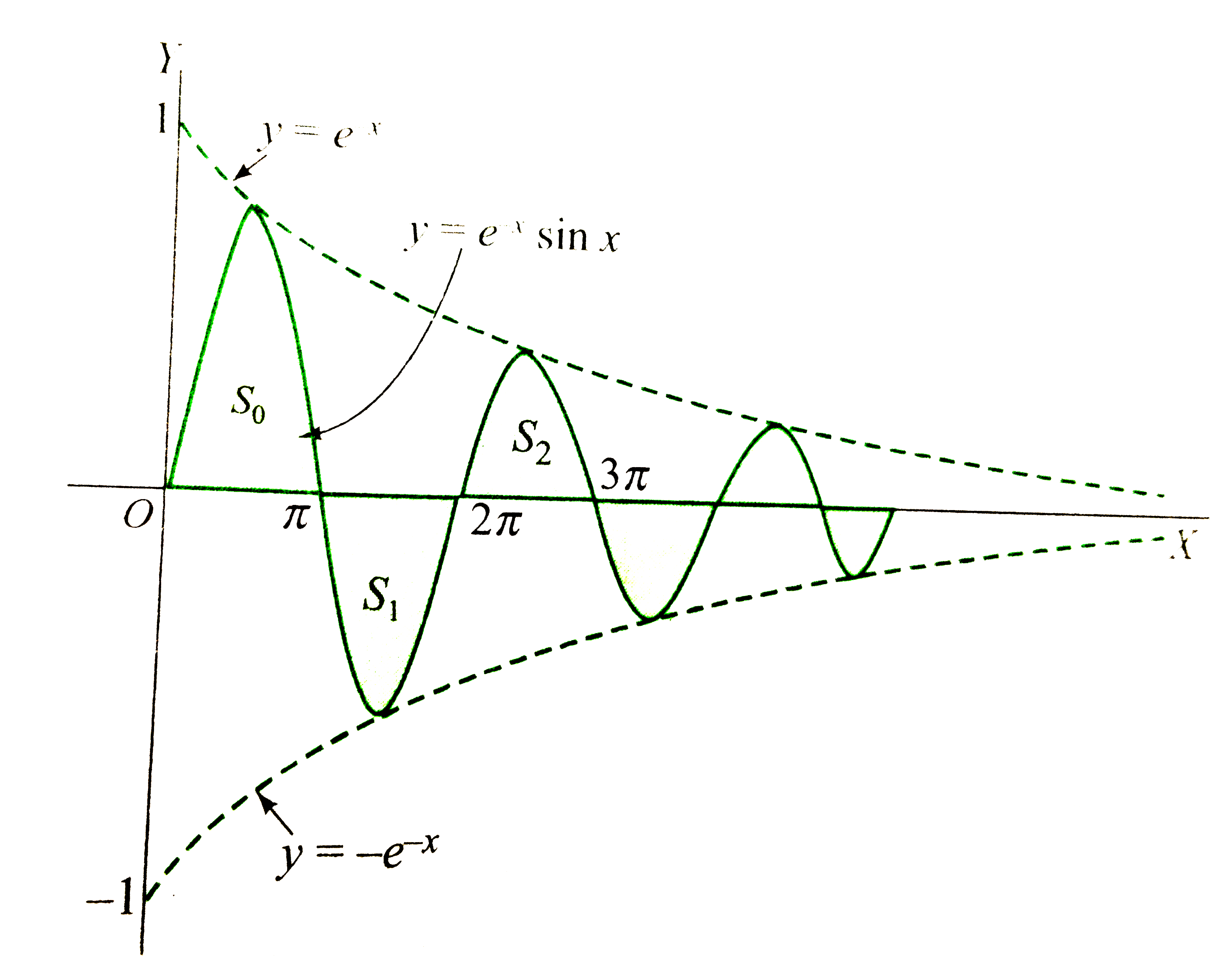
Also, the curve $y = e^{- x} \sin x$ intersects the positive semi-axis OX at the points where sin x=0, where $x_{n} = n π, n \in Z .$
$Also | y_{n} | = | y coordinate in the half-wave S_{n} |$
$∴ S_{n} = {(- 1)}^{n} \overset{(n + 1) π}{\int_{n π}} e^{- x} \sin x d x$
$= \frac{{(- 1)}^{n + 1}}{2} {[e^{- x} (- \sin x + \cos x)]}_{n π}^{(n + 1) π}$
$= \frac{{(- 1)}^{n + 1}}{2} [e^{- (n + 1) x} {(- 1)}^{n + 1} - e^{n π} {(- 1)}^{n}]$
$= \frac{e^{- n π}}{2} (1 + e^{π})$
$\Rightarrow \frac{S_{n + 1}}{S_{n}} = e^{- π}$
$and S_{0} = \frac{1}{2} (1 + e^{π}) .$
Therefore, the sequence $S_{0}, S_{1}, S_{2}, ...$ forms an infinite G.P. with common ratio $e^{- π}$ . we have
$\overset{\infty}{\underset{n = 0}{Σ}} S_{n} = \frac{\frac{1}{2} (1 + e^{π})}{1 - e^{- π}}$

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

CENGAGE-AREA-Exercise (Comprehension)

Home
Ask Doubt
Profile