$Two curves C_{1} \equiv {[f (y)]}^{2 / 3} + {[f (x)]}^{1 / 3} = 0 and C_{2} \equiv {[f (y)]}^{2 / 3} + {[f (x)]}^{2 / 3} = 12, satisfying the relation (x - y) f (x + y) - (x + y) f (x - y) = 4 x y (x^{2} - y^{2})$
The area bounded by $C_{1} and C_{2}$ is

A

$2 π - \sqrt{3}$ sq. units

B

$2 π + \sqrt{3}$ sq. units

C

$π + \sqrt{6}$ sq. units

D

$2 \sqrt{3} - π$ sq. units

Text Solution

Verified by Experts

The correct Answer is:B

Given
$(x - y) f (x + y) - (x + y) f (x - y) = 4 z y (x^{2} - y^{2})$
$= (x^{2} - y^{2}) [{(x + y)}^{2} - {(x - y)}^{2}]$
$= (x - y) {(x + y)}^{3} - (x + y) {(x - y)}^{3}$
$\Rightarrow f (x + y) = {(x + y)}^{3} \Rightarrow f (x) = x^{3}, f (y) = y^{3}$
Now equations of given curves are
$y^{2} + x = 0 ...(1)$
$x^{2} + y^{2} = 12 ...(2)$

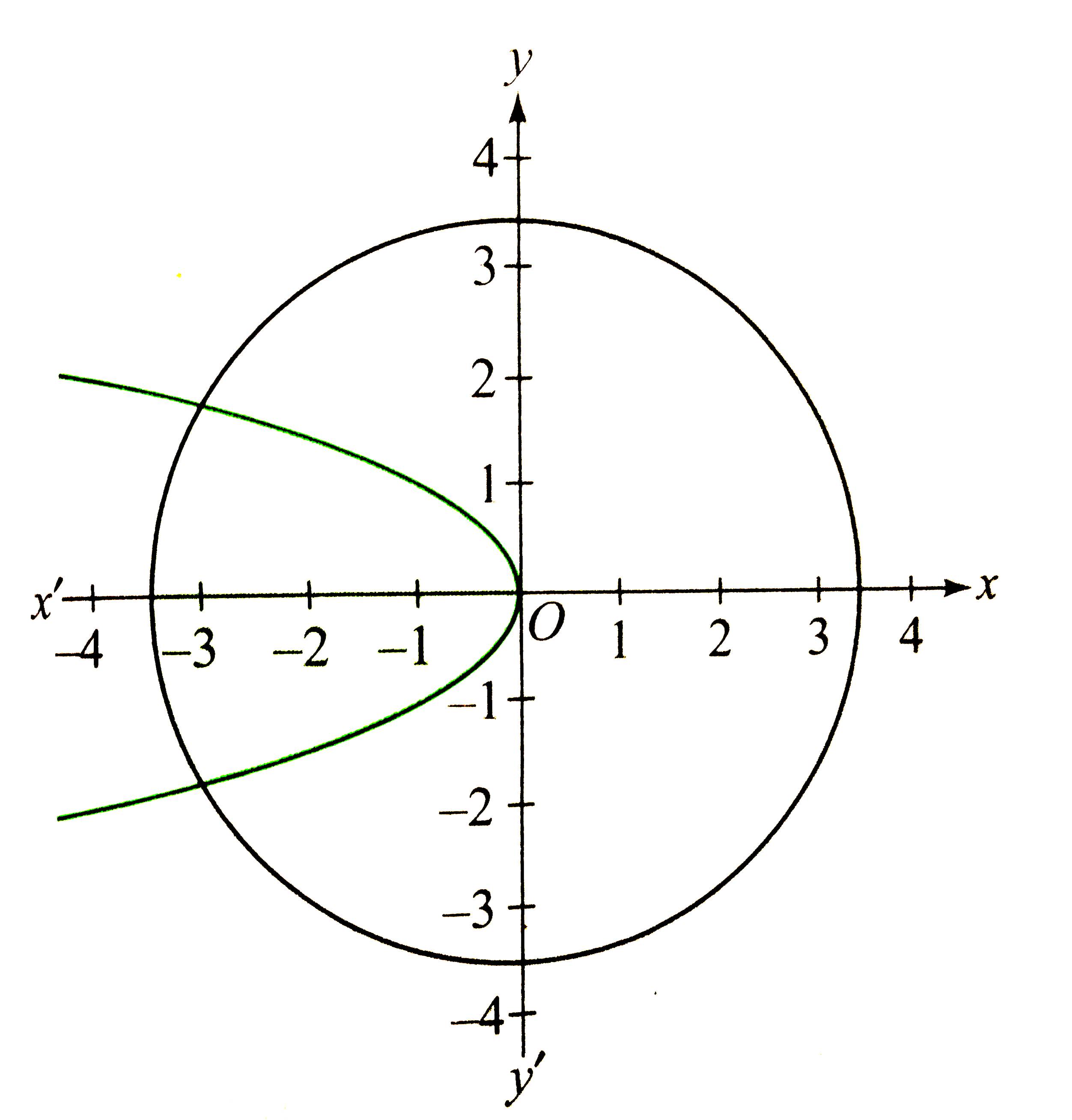
Solving equations (1) and (2), we get $x = - 3, y = \pm \sqrt{3}$
The area bounded by curves
$A = 2 ⎡ ⎢ ⎢ ⎣ ∣ ∣ ∣ ∣ ∣ - 3 \int - 2 \sqrt{3} d x ∣ ∣ ∣ ∣ ∣ + ∣ ∣ ∣ ∣ ∣ 0 \int - 3 \sqrt{- x} d x ∣ ∣ ∣ ∣ ∣ ⎤ ⎥ ⎥ ⎦$
$I_{1} = 2 - 3 \int - 2 \sqrt{3} \sqrt{12 - x^{2}} d x = 2 - π / 3 \int - π / 2 12 {cos}^{2} θ d θ$
$= 12 ⎡ ⎢ ⎢ ⎣ - π / 3 \int - π / 2 (1 + cos 2 θ) d θ ⎤ ⎥ ⎥ ⎦$
$= 12 {[θ + \frac{sin θ}{2}]}_{- π / 2}^{- π / 3} = 12 [- \frac{π}{3} - \frac{\sqrt{3}}{4} + \frac{π}{2}]$
$= 12 [\frac{π}{6} - \frac{\sqrt{3}}{4}] = 2 π - 3 \sqrt{3} .$
$I_{2} = 2 0 \int - 3 \sqrt{- x} d x = \frac{2 {[{(- x)}^{3 / 2}]}_{- 3}^{3 / 2}}{- 3 / 2} = - \frac{4}{3} [10 - 3^{3 / 2}] = 4 \sqrt{3} .$
$A = 2 π - 3 \sqrt{3} + 4 \sqrt{3} = 2 π + \sqrt{3}$ sq. units.

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
$Two curves C_{1} \equiv {[f (y)]}^{2 / 3} + {[f (x)]}^{1 / 3} = 0 and C_{2} \equiv {[f (y)]}^{2 / 3} + {[f (x)]}^{2 / 3} = 12, satisfying the relation (x - y) f (x + y) - (x + y) f (x - y) = 4 x y (x^{2} - y^{2})$
The area bounded by $C_{1} and x + y + 2 = 0$ is
A $5 / 2$ sq. units
B $7 / 2$ sq. units
C $9 / 2$ sq. units
DNone of these
Question 2 - Select One
$Two curves C_{1} \equiv {[f (y)]}^{2 / 3} + {[f (x)]}^{1 / 3} = 0 and C_{2} \equiv {[f (y)]}^{2 / 3} + {[f (x)]}^{2 / 3} = 12, satisfying the relation (x - y) f (x + y) - (x + y) f (x - y) = 4 x y (x^{2} - y^{2})$
The area bounded by the curve $C_{2} and | x | + | y | = \sqrt{12}$ is
A $12 π - 24$ sq. units
B $6 - \sqrt{12}$ sq. units
C $2 \sqrt{12} - 6$ sq. units
DNone of these
Question 3 - Select One
If f(y) = $2 y^{2}$ + by + c and f(0) = 3 and f(2) = 1, then the value of f(1) is
A0
B1
C2
D3

CENGAGE-AREA-Exercise (Comprehension)

Home
Ask Doubt
Profile