If y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
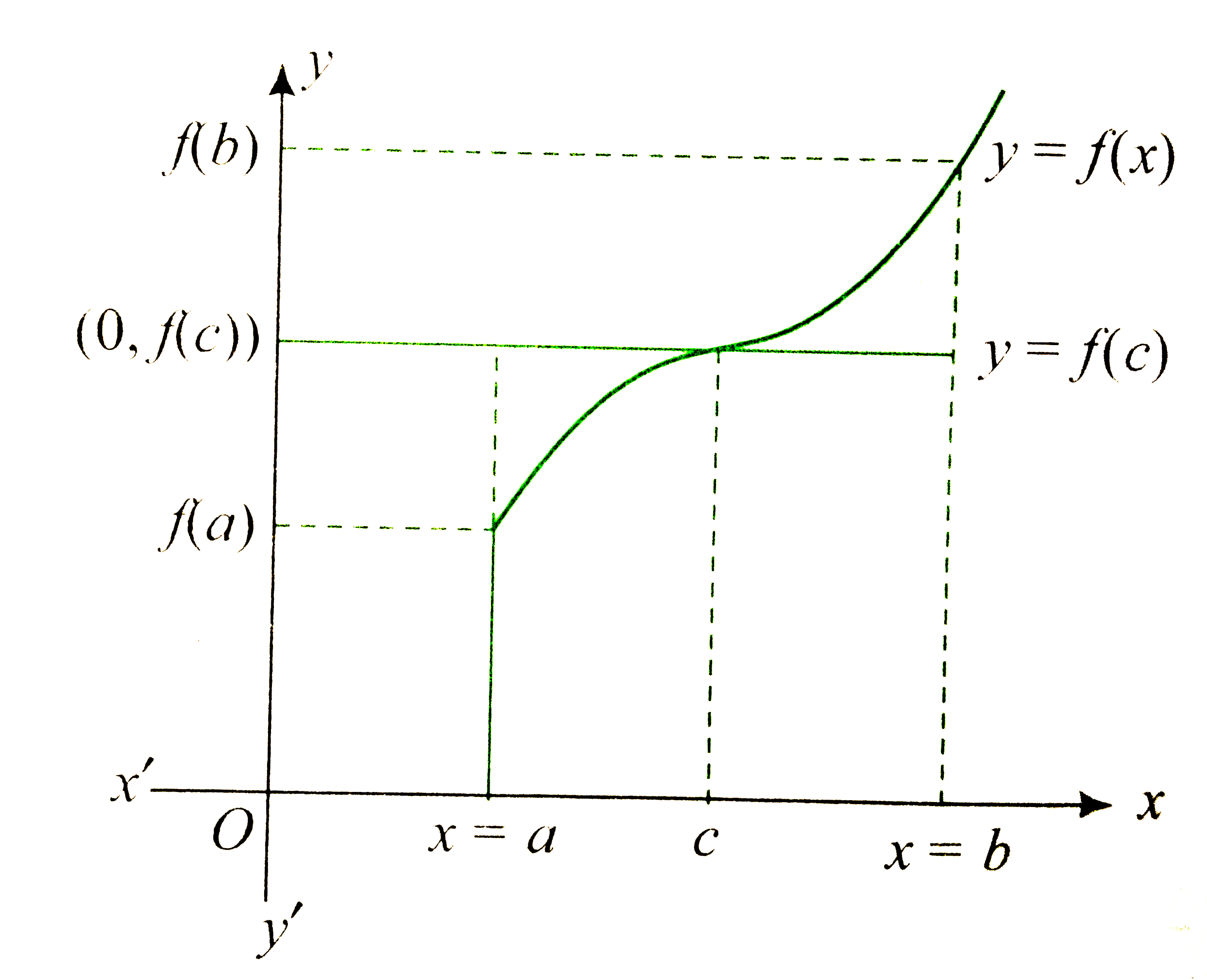
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
The value of the parameter a for which the area of the figure bounded by the abscissa axis, the graph of the function y=x3+3x2+x+a, and the straight lines, which are parallel to the axis of ordinates and cut the abscissa axis at the point of extremum of the function, which is the least, isSolution in Tamil
2
0
-1
1
The correct Answer is:C
f(x)=x3+3x2+x+a
f'(x)=3x2+6x+1=0
⇒ x=−1±√63.
Hence, f(x) cuts the x-axis at
12[(−1+√63)+(−1−√63)]=−1.
f(−1)=−1+3−1+a=0
a=−1.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Matrix)4videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Numerical)16videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Multiple)10videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank10videos
AREA UNDER CURVES
Similar Questions
Match the following lists :
 01:45View Solution
01:45View SolutionThe area enclosed by the curve C:y=x√9−x2(x≥0) and the x-axis is___.
01:40View SolutionLet A(k) be the area bounded by the curves y=x2−3 and y=kx+2 The range of A(k) is (10√53,∞) The range of A(k) is (20√53,∞) If function k→A(k) is defined for k∈[−2,∞ ), then A(k) is many-one function. The value of k for which area is minimum is 1.
01:25View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
02:33View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionLet the definite integral be defined by the formula ∫baf(x)dx=b−a2(f(a)+f(b)). For more accurate result, for cε(a,b), we can use ∫baf(x)dx=∫caf(x)dx+∫bcf(x)dx=F(c) so that for c=a+b2 we get ∫baf(x)dx=b−a4(f(a)+f(b)+2f(c)).
If f''(x)<0∀xε(a,b) and c is a point such that a<c<b, and (c,f(c)) is the point lying on the curve for which F(c) is maximum then f'(c) is equal to02:00View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
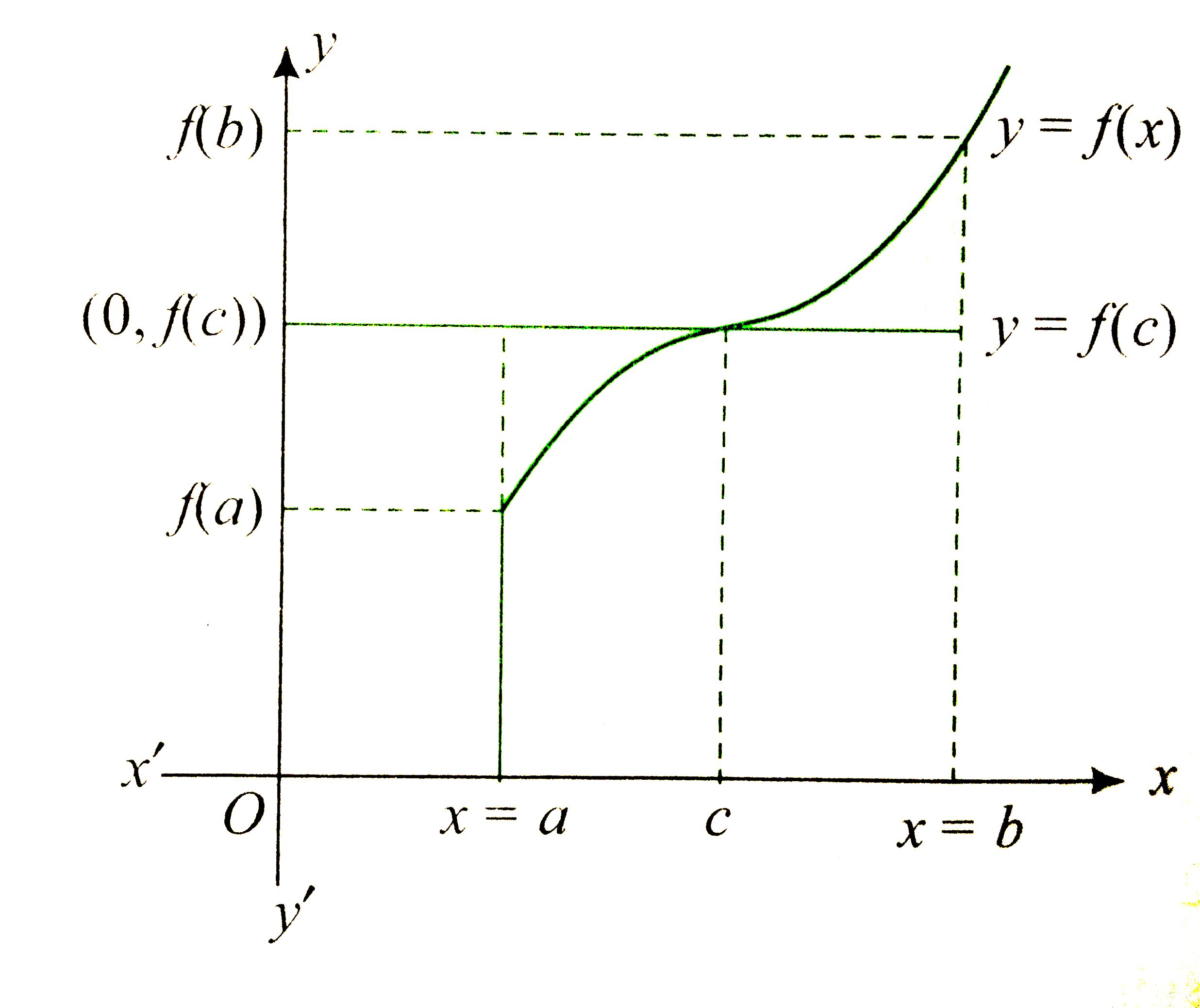
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
If the area bounded by f(x)=x33−x2+a and the straight lines x=0, x=2, and the x-axis is minimum, then the value of a is06:03View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx

Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
The value of the parameter a for which the area of the figure bounded by the abscissa axis, the graph of the function y=x3+3x2+x+a, and the straight lines, which are parallel to the axis of ordinates and cut the abscissa axis at the point of extremum of the function, which is the least, is08:34View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
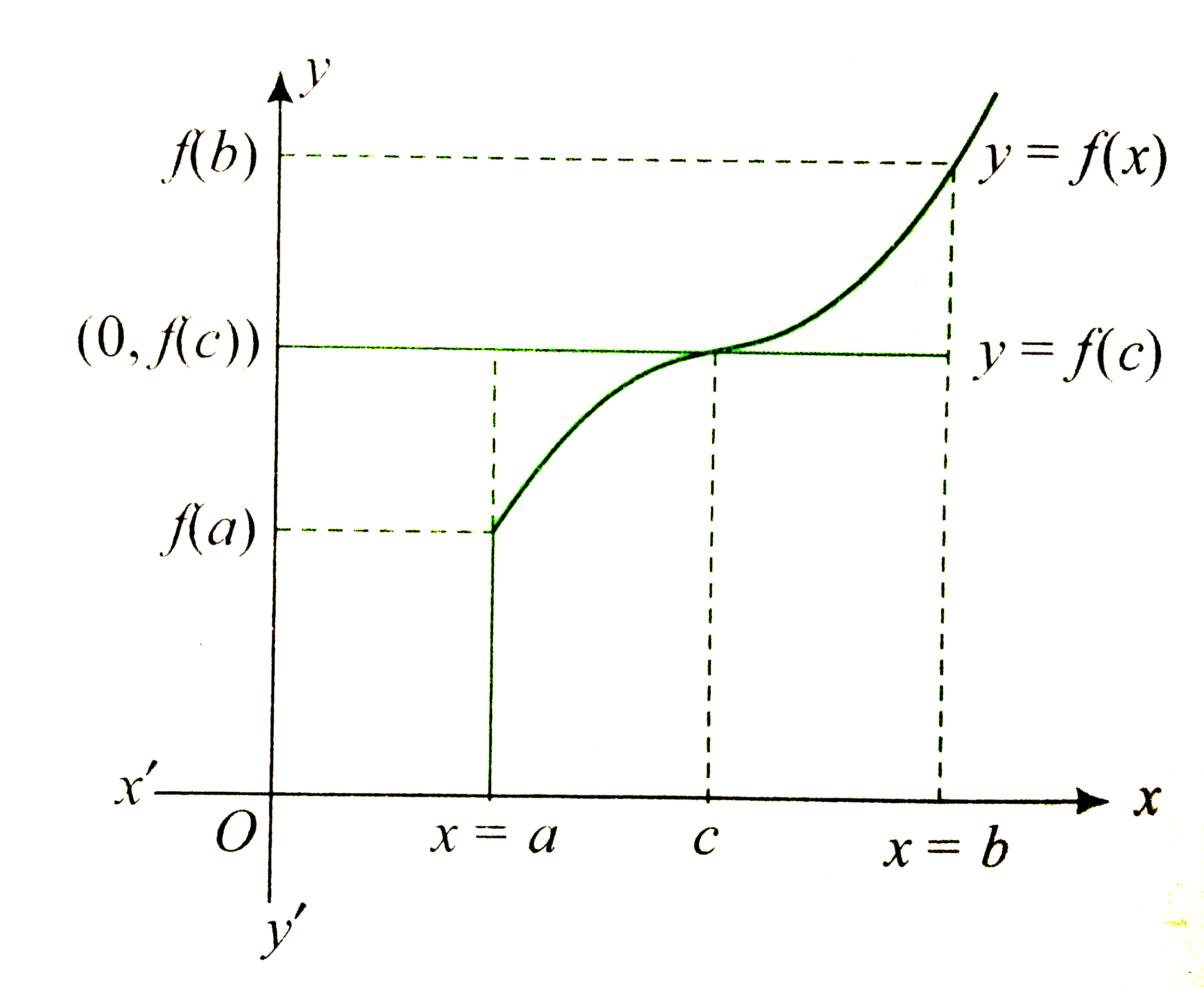
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
If the area enclosed by f(x)=sinx+cosx,y=a between two consecutive points of extremum is minimum, then the value of a is03:21View SolutionIf ∫b−c0f(x+c)dx=a∫cbf(x)dx, then a =
03:46View SolutionIf ∫b−c0f(x+c)dx=k∫cbf(x)dx then k=
03:54View SolutionLet the definite integral be defined by the formula ∫baf(x)dx=b−a2(f(a)+f(b)). For more accurate result, for cε(a,b), we can use ∫baf(x)dx=∫caf(x)dx+∫bcf(x)dx=F(c) so that for c=a+b2 we get ∫baf(x)dx=b−a4(f(a)+f(b)+2f(c)).
If f''(x)<0∀xε(a,b) and c is a point such that a<c<b, and (c,f(c)) is the point lying on the curve for which F(c) is maximum then f'(c) is equal to03:21View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx

Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
If the area bounded by f(x)=x33−x2+a and the straight lines x=0, x=2, and the x-axis is minimum, then the value of a is02:58View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b))isminiμmwhen
c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx

Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
The value of the parameter a for which the area of the figure bounded by the abscissa axis, the graph of the function y=x3+3x2+x+a, and the straight lines, which are parallel to the axis of ordinates and cut the abscissa axis at the point of extremum of the function, which is the least, is03:45View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx

Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
If the area enclosed by f(x)=sinx+cosx,y=a between two consecutive points of extremum is minimum, then the value of a is06:54View Solution

