Two curves C_(1)equiv[f(y)]^(2//3)+[f(x)]^(1//3)=0 and C_(2)equiv[f(y)]^(2//3)+[f(x)]^(2//3)=12, satisfying the relation "(x-y)f(x+y)-(x+y)f(x-y)=4xy(x^(2)-y^(2))
The area bounded by C_(1) and x+y+2=0 isSolution in Tamil
5/2 sq. units
7/2 sq. units
9/2 sq. units
None of these
The correct Answer is:C
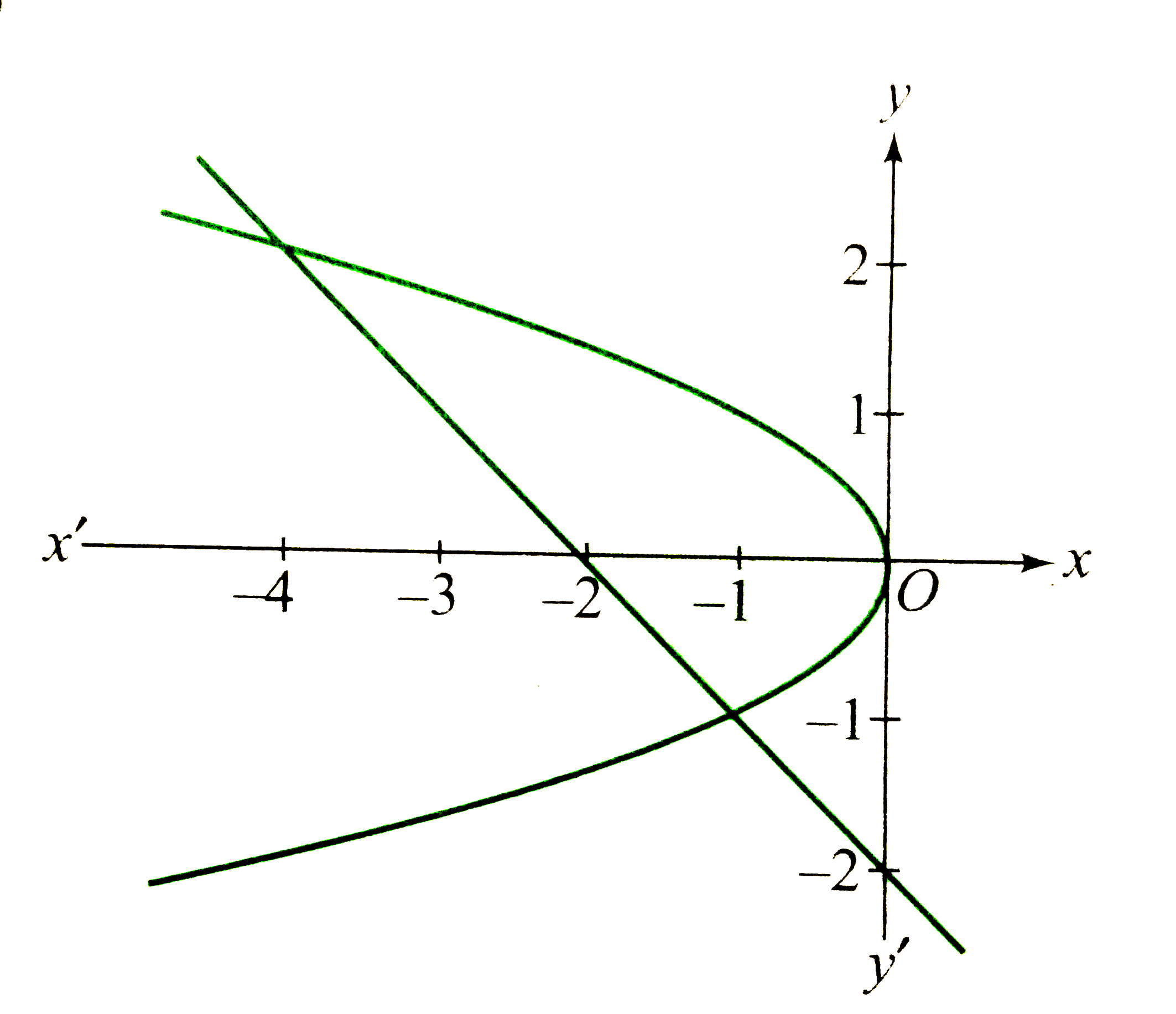
Required area =2∫−1(−y2−(−y−2))dy
=[y22+2y−y33]21
=[42+4−83−(12−2+13)]
=9/2 sq. units.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Matrix)4videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Numerical)16videos
AREA
- BOOK - CENGAGECHAPTER - AREAEXERCISE - Exercise (Multiple)10videos
AREA
- BOOK - CENGAGECHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGECHAPTER - AREA UNDER CURVESEXERCISE - Question Bank10videos
AREA UNDER CURVES
Similar Questions
Match the following lists :
 08:07View Solution
08:07View SolutionThe area enclosed by the curve C:y=x√9−x2(x≥0) and the x-axis is___.
05:23View SolutionLet A(k) be the area bounded by the curves y=x2−3 and y=kx+2 The range of A(k) is (10√53,∞) The range of A(k) is (20√53,∞) If function k→A(k) is defined for k∈[−2,∞ ), then A(k) is many-one function. The value of k for which area is minimum is 1.
03:04View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionThe area of the region (s) enclosed by the curves y=x2 and y=√|x| is
View SolutionIf a function satisfies (x−y)f(x+y)−(x+y)f(x−y)=2(x2y−y3)∀x,y∈Randf(1)=2, then
View SolutionIf a curve y=f(x) satisfies y''x^(2)+x(y')^(2)=2xy',f(0)=0 and f'(1)=1 then f(x) is
06:07View Solution|f(x)-f(y)|<=2|x-y|^(3/2);f(0)=1, then int_(0)^(1)f^(2)(x)backslash dx
10:55View SolutionTwo curves C1≡[f(y)]2/3+[f(x)]1/3=0andC2≡[f(y)]2/3+[f(x)]2/3=12, satisfying the relation (x−y)f(x+y)−(x+y)f(x−y)=4xy(x2−y2)
The area bounded by C1andC2 is12:34View SolutionTwo curves C1≡[f(y)]2/3+[f(x)]1/3=0andC2≡[f(y)]2/3+[f(x)]2/3=12, satisfying the relation (x−y)f(x+y)−(x+y)f(x−y)=4xy(x2−y2)
The area bounded by the curve C2and|x|+|y|=√12 is04:51View SolutionTwo curves C1≡[f(y)]2/3+[f(x)]1/3=0andC2≡[f(y)]2/3+[f(x)]2/3=12, satisfying the relation (x−y)f(x+y)−(x+y)f(x−y)=4xy(x2−y2)
The area bounded by C1andx+y+2=0 is06:16View SolutionIf C1≡y=11+x2andC2≡y=x22 be two curve lying in XY plane. Then
View Solutionमान लीजिये f:R→R में एक अवकलनीय फलन है जो प्रतिबन्ध को सन्तुष्ट करता है
f.(x+y3)=2+f(x)+f(y)3,∀x,y∈Rतथा f'(2)=2
यदि g(x)=|f(|x|)−3|,Ax∈R हो, तो g(x) के लिए02:39View SolutionTwo curves C1≡[f(y)]2/3+[f(x)]1/3=0andC2≡[f(y)]2/3+[f(x)]2/3=12, satisfying the relation (x−y)f(x+y)−(x+y)f(x−y)=4xy(x2−y2)
The area bounded by the curve C1andC2 isView SolutionTwo curves C1≡[f(y)]2/3+[f(x)]1/3=0andC2≡[f(y)]2/3+[f(x)]2/3=12, satisfying the relation (x−y)f(x+y)−(x+y)f(x−y)=4xy(x2−y2)
The area bounded by the curve C2and|x|+|y|=√12 is02:13View SolutionTwo curves C1≡[f(y)]2/3+[f(x)]1/3=0andC2≡[f(y)]2/3+[f(x)]2/3=12, satisfying the relation (x−y)f(x+y)−(x+y)f(x−y)=4xy(x2−y2)
The area bounded by C1andx+y+2=0 is08:43View Solution

