Draw the graph of the relation y2(x−1)=x2(1+x) Solution in Tamil
Video Solution
Text Solution
We have y2(x−1)=x2(1+x)
or y=±x√x+1x−1
Let us first draw the graph of y=f(x)=x√x+1x−1
Clearly,the domain of the function is (−∞,−1)∪(1,∞)
f(x)=0∴x=0,1
So the graph meets the x-axis at (0,0) and (−1,0).
Also, f(x)≥0 for x≥1 and f(x)<0 for x<−1
f′(x)=1.√x+1x−1+xx−1−(x+1)(x−1)22√x+1x−1
=x2−x−1(x−1)2√x+1x−1
=(x−11−√52)(x−1+√52)(x−1)2√x+1x−1
f′(x)=0∴x=1+√52, which is the point of minima.
x=1−√52 is not a critical point as −1<1−√52<1
f(x) decreases for (−∞,−1)∪(1,1+√52)
f(x) increases for 1+√52,∞
Also xx→1+√x+1x−1=∞
So the graph of y=f(x)=x√x+1x−1 is as shown in the following figure.
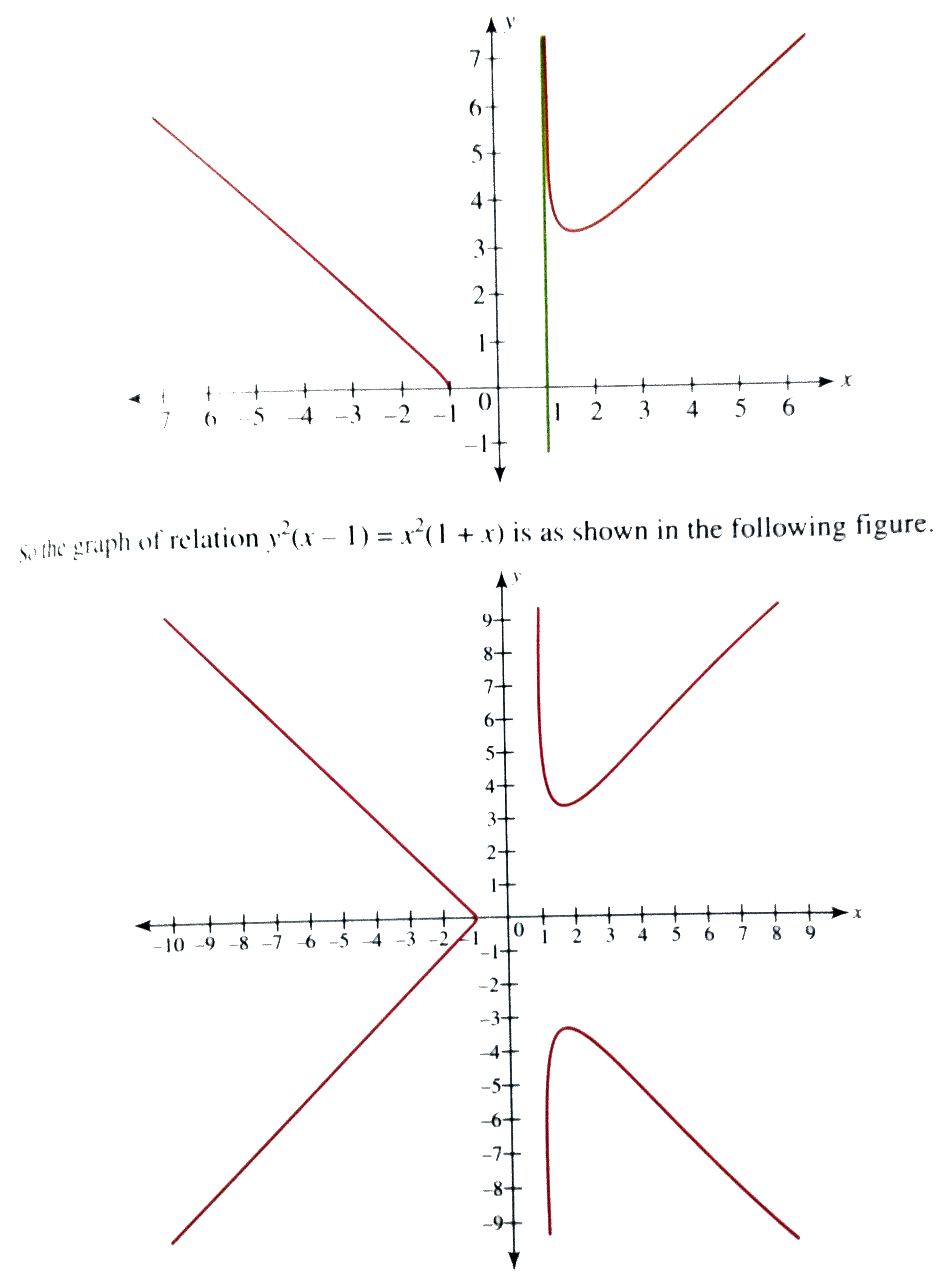
So the graph of relation y2(x−1)=x2(1+x) is as shown in the following figure.

|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Draw the graph of y=sin2x−cosx
04:14View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
01:18View SolutionSolve: (x+2)3=2x(x2−1)
View SolutionDraw the graph of y=x−1x2 and hence the graph of y=|x−1|x2.
04:25View SolutionDraw the graph of y=x−1x−2.
03:58View SolutionDraw the graph of the relation y2=x2(1−x)
02:16View SolutionDraw the graph of the relation y2(x−1)=x2(1+x)
03:14View SolutionDraw the graph of the relation y=|x|√1−x2
03:03View SolutionDraw the graph of y=x−1x2 and hence the graph of y=|x−1|x2.
05:20View SolutionDraw graph of y=1x2−x.
06:32View SolutionDraw the graph of y=x−1x−2.
04:33View SolutionDraw the graph of the relation y2=x2(1−x)
02:24View SolutionDraw the graph of the relation y2(x−1)=x2(1+x)
03:59View SolutionDraw the graph of the relation y=|x|√1−x2
10:04View SolutionDraw graph of y=(1)/(x^(2))-x .
05:36View Solution

