State whether the statements are true (T) or (F) false.
If opposite angles of a quadrilateral are equal, it must be a parallelogram.
To determine whether the statement "If opposite angles of a quadrilateral are equal, it must be a parallelogram" is true or false, we can follow these steps:
1. Understanding the Statement: The statement claims that if a quadrilateral has equal opposite angles, then it must be classified as a parallelogram.
2. Define a Quadrilateral: A quadrilateral is a four-sided polygon. It can have various shapes, including rectangles, squares, trapezoids, and irregular quadrilaterals.
3. Identify Opposite Angles: Let's denote the angles of the quadrilateral as A, B, C, and D. According to the statement, we have:
- Angle A = Angle C (opposite angles)
- Angle B = Angle D (opposite angles)
4. Properties of a Parallelogram: In a parallelogram, opposite angles are equal. Therefore, if we can show that having equal opposite angles implies that the quadrilateral is a parallelogram, we can conclude that the statement is true.
5. Using Co-Interior Angles: For a quadrilateral to be a parallelogram, we can use the property of co-interior angles:
- If two lines are parallel, then the sum of the co-interior angles is equal to 180 degrees.
- Let's assume that sides AB and CD are parallel, and sides AD and BC are also parallel.
6. Establishing Relationships: If we have:
- Angle A + Angle B = 180 degrees (co-interior angles)
- Angle C + Angle D = 180 degrees (co-interior angles)
Since Angle A = Angle C and Angle B = Angle D, we can substitute:
- Angle A + Angle D = 180 degrees
- Angle B + Angle C = 180 degrees
7. Conclusion: Since we have established that the opposite angles are equal and the co-interior angles add up to 180 degrees, we can conclude that the quadrilateral must be a parallelogram.
8. Final Answer: Therefore, the statement "If opposite angles of a quadrilateral are equal, it must be a parallelogram" is True (T).
- Angle A = Angle C (opposite angles)
- Angle B = Angle D (opposite angles)
- If two lines are parallel, then the sum of the co-interior angles is equal to 180 degrees.
- Let's assume that sides AB and CD are parallel, and sides AD and BC are also parallel.
- Angle A + Angle B = 180 degrees (co-interior angles)
- Angle C + Angle D = 180 degrees (co-interior angles)
- Angle A + Angle D = 180 degrees
- Angle B + Angle C = 180 degrees
Topper's Solved these Questions
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBook:NCERT EXEMPLARChapter:UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYExercise:APPLICATIONS, GAMES AND PUZZLES
Explore 3 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBook:NCERT EXEMPLARChapter:UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYExercise:THINK AND DISCUSS
Explore 2 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBook:NCERT EXEMPLARChapter:UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYExercise:THINK AND DISCUSS
Explore 2 Videos
- SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTBook:NCERT EXEMPLARChapter:SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTExercise:Exercise
Explore 52 Videos
- VISUALISING SOLID SHAPES Book:NCERT EXEMPLARChapter:VISUALISING SOLID SHAPES Exercise:EXERCISE
Explore 91 Videos
Similar Questions
State whether the statements are true (T) or (F) false.
If diagonals of a quadrilateral are equal, it must be a rectangle.
View SolutionState whether the statements are true (T) or (F) false.
If diagonals of a quadrilateral bisect each other, it must be a parallelogram.
View SolutionState whether the statements are true (T) or (F) false.
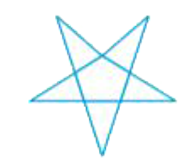 is a polygon.
is a polygon.
View SolutionState whether the statements are true (T) or (F) false.
Rectangle is a regular quadrilateral.
View SolutionState whether the statements are true (T) or (F) false.
A kite is not a convex quadrilateral.
View SolutionState whether the statements are true (T) or (F) false.
Sum of all the angles of a quadrilateral is 180°.
View SolutionState whether the statements are true or falsea−b=b−a
View SolutionState whether the statements are true or falsea×b=b×a
View SolutionState whether the statements are true or falsea÷a=b÷a
View SolutionState whether the statements are true (T) or (F) false.
All kites are squares.
View Solution