State whether the statements are true (T) or (F) false.
Every parallelogram is a rectangle.
To determine whether the statement "Every parallelogram is a rectangle" is true or false, we need to analyze the definitions and properties of both parallelograms and rectangles.
1. Definition of a Parallelogram:
A parallelogram is a quadrilateral where opposite sides are parallel and equal in length. Additionally, the diagonals bisect each other, and opposite angles are equal.
2. Definition of a Rectangle:
A rectangle is a specific type of parallelogram where all four angles are right angles (90 degrees). In a rectangle, opposite sides are also parallel and equal, and the diagonals are equal in length.
3. Comparison of Properties:
- All rectangles are parallelograms because they satisfy the properties of a parallelogram (opposite sides are parallel and equal, diagonals bisect each other).
- However, not all parallelograms are rectangles because parallelograms do not necessarily have right angles. A parallelogram can have angles that are not 90 degrees.
4. Conclusion:
Since there exist parallelograms that do not have all angles equal to 90 degrees, the statement "Every parallelogram is a rectangle" is false.
Final Answer:
The statement "Every parallelogram is a rectangle" is False (F).
---
A parallelogram is a quadrilateral where opposite sides are parallel and equal in length. Additionally, the diagonals bisect each other, and opposite angles are equal.
A rectangle is a specific type of parallelogram where all four angles are right angles (90 degrees). In a rectangle, opposite sides are also parallel and equal, and the diagonals are equal in length.
- All rectangles are parallelograms because they satisfy the properties of a parallelogram (opposite sides are parallel and equal, diagonals bisect each other).
- However, not all parallelograms are rectangles because parallelograms do not necessarily have right angles. A parallelogram can have angles that are not 90 degrees.
Since there exist parallelograms that do not have all angles equal to 90 degrees, the statement "Every parallelogram is a rectangle" is false.
The statement "Every parallelogram is a rectangle" is False (F).
Topper's Solved these Questions
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - APPLICATIONS, GAMES AND PUZZLES
3 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - THINK AND DISCUSS
2 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - THINK AND DISCUSS
2 Videos
- SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTBOOK - NCERT EXEMPLARCHAPTER - SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTEXERCISE - Exercise
52 Videos
- VISUALISING SOLID SHAPES BOOK - NCERT EXEMPLARCHAPTER - VISUALISING SOLID SHAPES EXERCISE - EXERCISE
91 Videos
Similar Questions
State whether the statements are true (T) or (F) false.
Every trapezium is a rectangle.
View SolutionState whether the statements are true (T) or (F) false.
Every kite is a parallelogram.
View SolutionState whether the statements are true (T) or (F) false.
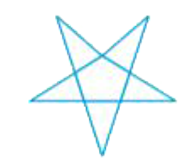 is a polygon.
is a polygon.
View SolutionState whether the statements are true (T) or (F) false.
Every square is a trapezium.
View SolutionState whether the statements are true (T) or (F) false.
Every rhombus is a trapezium.
View SolutionState whether the statements are true (T) or (F) false.
Every rectangle is a trapezium.
View SolutionState whether the statements are true (T) or (F) false.
Every square is a parallelogram.
View SolutionState whether the statements are true (T) or (F) false.
Every square is a rhombus.
View SolutionState whether the statements are true or falsea−b=b−a
View SolutionState whether the statements are true or falsea×b=b×a
View Solution
