State whether the statements are true (T) or (F) false.
Every square is a parallelogram.
To determine whether the statement "Every square is a parallelogram" is true or false, we can analyze the properties of both squares and parallelograms.
1. Definition of a Square:
A square is a type of quadrilateral where all four sides are equal in length, and all four angles are right angles (90 degrees). Additionally, the diagonals of a square are equal in length and bisect each other at right angles.
2. Definition of a Parallelogram:
A parallelogram is a quadrilateral with opposite sides that are both parallel and equal in length. The opposite angles are also equal, and the diagonals bisect each other.
3. Comparison of Properties:
- Sides: In a square, all sides are equal. In a parallelogram, opposite sides are equal, but not necessarily all four sides.
- Angles: In a square, all angles are 90 degrees. In a parallelogram, opposite angles are equal, but they can be any angle that satisfies the property of parallel sides.
- Diagonals: In a square, the diagonals are equal and bisect each other at right angles. In a parallelogram, the diagonals bisect each other, but they are not necessarily equal.
4. Conclusion:
Since a square satisfies all the properties of a parallelogram (opposite sides are equal and parallel), we can conclude that every square is indeed a parallelogram.
Thus, the statement "Every square is a parallelogram" is True (T).
A square is a type of quadrilateral where all four sides are equal in length, and all four angles are right angles (90 degrees). Additionally, the diagonals of a square are equal in length and bisect each other at right angles.
A parallelogram is a quadrilateral with opposite sides that are both parallel and equal in length. The opposite angles are also equal, and the diagonals bisect each other.
- Sides: In a square, all sides are equal. In a parallelogram, opposite sides are equal, but not necessarily all four sides.
- Angles: In a square, all angles are 90 degrees. In a parallelogram, opposite angles are equal, but they can be any angle that satisfies the property of parallel sides.
- Diagonals: In a square, the diagonals are equal and bisect each other at right angles. In a parallelogram, the diagonals bisect each other, but they are not necessarily equal.
Since a square satisfies all the properties of a parallelogram (opposite sides are equal and parallel), we can conclude that every square is indeed a parallelogram.
Topper's Solved these Questions
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - APPLICATIONS, GAMES AND PUZZLES
3 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - THINK AND DISCUSS
2 Videos
- UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - UNDERSTANDING QUADRILATERALS AND PRACTICAL GEOMETRYEXERCISE - THINK AND DISCUSS
2 Videos
- SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTBOOK - NCERT EXEMPLARCHAPTER - SQUARE - SQUARE ROOT AND CUBE-CUBE ROOTEXERCISE - Exercise
52 Videos
- VISUALISING SOLID SHAPES BOOK - NCERT EXEMPLARCHAPTER - VISUALISING SOLID SHAPES EXERCISE - EXERCISE
91 Videos
Similar Questions
State whether the statements are true (T) or (F) false.
Every trapezium is a parallelogram.
View SolutionState whether the statements are true (T) or (F) false.
Every kite is a parallelogram.
View SolutionState whether the statements are true (T) or (F) false.
Every square is a trapezium.
View SolutionState whether the statements are true (T) or (F) false.
Every square is a rhombus.
View SolutionState whether the statements are true (T) or (F) false.
All rectangles are parallelograms.
View Solutionstate whether the statement are true (T) or false (F).
Every kite is a parallelogram.
View SolutionState whether the statements are true (T) or (F) false.
All kites are squares.
View SolutionState whether the statements are true (T) or (F) false.
All squares are rectangles.
View SolutionState whether the statements are true (T) or (F) false.
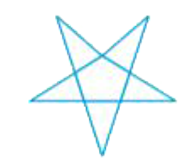 is a polygon.
is a polygon.
View SolutionState whether the statements are true (T) or (F) false.
Every rhombus is a trapezium.
View Solution
