In a circle with center O and radius 10 cm, PQ and RS are two parallel chords of lengths x cm and 12 cm, respectively, and both the chords are on the opposite sides of O. If the distance between PQ and RS is 14 cm, the value of x is :
केंद्र O तथा त्रिज्या 10 सेमी वाले एक वृत्त में, PQ और RS दो समानांतर जीवाएं हैं जिनकी लंबाई क्रमशः x सेमी और 12 सेमी है | दोनों जीवाएं O के विपरीत दिशा में हैं| यदि PQ और RS के बीच की दूरी 14 सेमी है, तो x का मान ज्ञात करें |
a)16
b)20
c)15
d)18
To solve the problem, we will follow these steps:
Step 1: Understand the Geometry
We have a circle with center O and radius 10 cm. There are two parallel chords, PQ and RS, with lengths x cm and 12 cm respectively. The distance between the two chords is 14 cm.
Step 2: Set Up the Diagram
Draw a circle with center O and radius 10 cm. Mark the chords PQ and RS such that they are parallel and on opposite sides of the center O. Let the perpendicular distances from O to PQ and RS be OE and OF respectively.
Step 3: Use the Properties of Chords
Since OE is perpendicular to PQ, we can denote the half-length of PQ as PE = x/2. Similarly, since OF is perpendicular to RS, we denote the half-length of RS as RF = 12/2 = 6 cm.
Step 4: Relate the Distances
The total distance between the two chords is given as 14 cm. Therefore, we can express this as:
EF=OE+OF=14 cm
Step 5: Apply the Pythagorean Theorem
For triangle ORE:
- The hypotenuse OR = 10 cm (radius)
- The base RF = 6 cm
- The height OF is unknown.
Using the Pythagorean theorem:
OR2=OF2+RF2
102=OF2+62
100=OF2+36
OF2=100−36=64
OF=8 cm
Step 6: Find OE
Now we can find OE using the total distance:
OE+OF=14
OE+8=14
OE=14−8=6 cm
Step 7: Apply the Pythagorean Theorem Again
Now, we can apply the Pythagorean theorem to triangle OPE:
- The hypotenuse OP = 10 cm
- The height OE = 6 cm
- The base PE = x/2.
Using the Pythagorean theorem:
OP2=OE2+PE2
102=62+(x/2)2
100=36+(x/2)2
(x/2)2=100−36=64
x/2=8
x=16 cm
Final Answer
The value of x is 16 cm.
---
We have a circle with center O and radius 10 cm. There are two parallel chords, PQ and RS, with lengths x cm and 12 cm respectively. The distance between the two chords is 14 cm.
Draw a circle with center O and radius 10 cm. Mark the chords PQ and RS such that they are parallel and on opposite sides of the center O. Let the perpendicular distances from O to PQ and RS be OE and OF respectively.
Since OE is perpendicular to PQ, we can denote the half-length of PQ as PE = x/2. Similarly, since OF is perpendicular to RS, we denote the half-length of RS as RF = 12/2 = 6 cm.
The total distance between the two chords is given as 14 cm. Therefore, we can express this as:
EF=OE+OF=14 cm
For triangle ORE:
- The hypotenuse OR = 10 cm (radius)
- The base RF = 6 cm
- The height OF is unknown.
OR2=OF2+RF2
102=OF2+62
100=OF2+36
OF2=100−36=64
OF=8 cm
Now we can find OE using the total distance:
OE+OF=14
OE+8=14
OE=14−8=6 cm
Now, we can apply the Pythagorean theorem to triangle OPE:
- The hypotenuse OP = 10 cm
- The height OE = 6 cm
- The base PE = x/2.
OP2=OE2+PE2
102=62+(x/2)2
100=36+(x/2)2
(x/2)2=100−36=64
x/2=8
x=16 cm
The value of x is 16 cm.
Topper's Solved these Questions
Similar Questions
AB and CD are two parallel chords of a circle of lengths 10 cm and 4 cm respectively. If the chords are on the same side of the centre and the distance between them is 3cm, then the diameter of the circle is.
View SolutionAB and CD are two parallel chords of a circle such that AB=10cm and CD=24cm. If the chords are on the opposite sides of the centre and the distance between them is 17cm, find the radius of the circle.
View Solution
Knowledge Check
In a circle of radius 17 cm, two parallel chords of lengths 30 cm and 16 cm are drawn. If both the chords are on the same side of the centre, then the distance between the chords is a
A9 cmB7 cmC23 cmD11 cmAB and CD are two parallel chords of a circle such that AB=10cm and CD=24cm. If the chords are on the opposite sides of the centre and the distance between them is 17cm, find the radius of the circle.
A12 cmB13 cmC14 cmD16 cmPQ and RS are two parallel chords of a circle with centre C such that PQ = 8 cm and RS = 16 cm. If the chords are on the same side of the centre and the distance between them is 4 cm, then the radius of the circle is :
A3√2 cmB3√5 cmC4√5 cmD5√5 cm
AB and CD are two parallel chords of a circle such that AB=10 cm and CD=24 cm. If the chords are on the opposite sides of the centre and the distance between them is 17 cm, find the radius of the circle.
View SolutionIn a circle of radius 5 cm, AB and CD are two parallel chords of lengths 8 cm and 6 cm respectively. Calculate the distance between the chords if they are
(i) on the same side of the centre.
(ii) on the opposite sides of the centre.
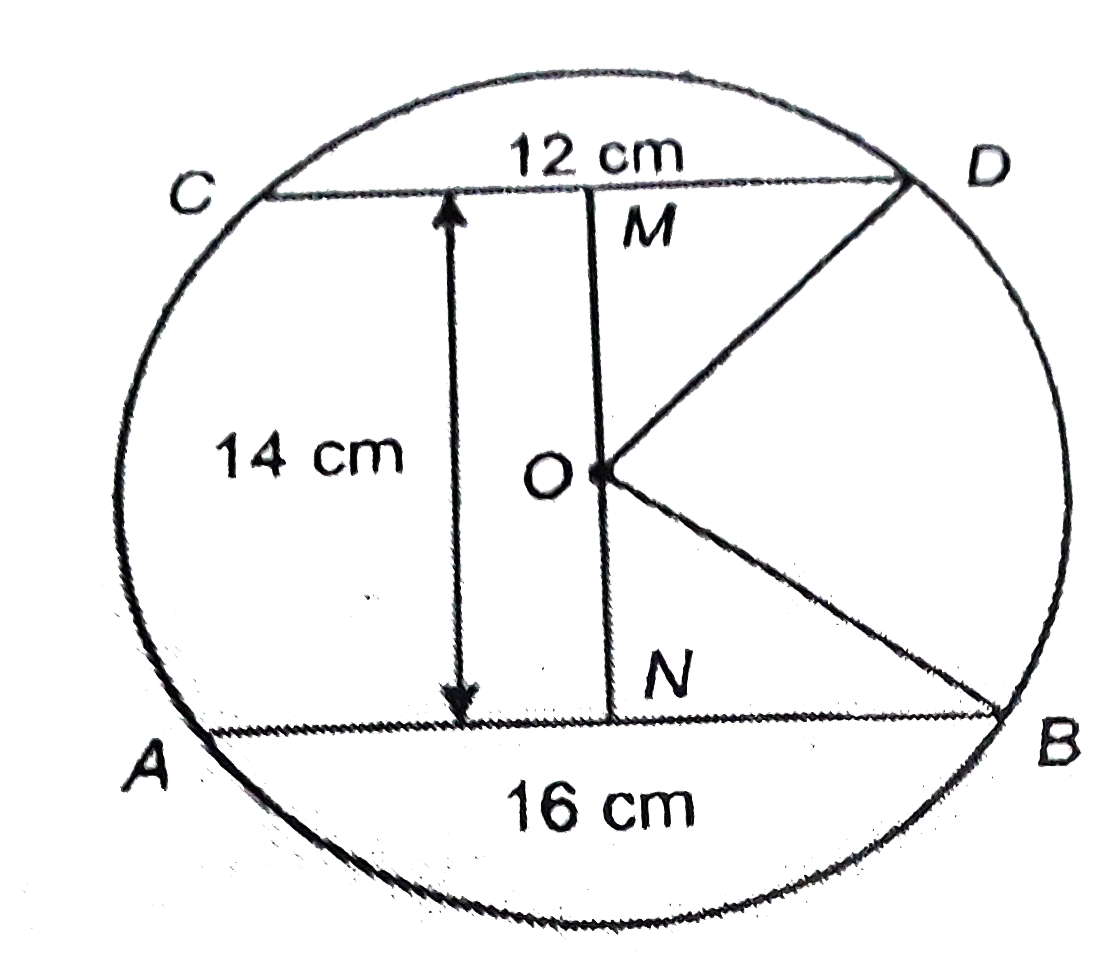
View SolutionIn the adjoining figure ,AB and CD are two parallel chords of a circle with centre O , whose length are 16 cm and 12 cm respectively. Find the radius of the circle if the distance between them is 14 cm.
View SolutionIn a circle of radius 10 cm, PQ and RS are two parallel chords of length 16 cm and 12 cm respectively. What is the distance between the chords if they are on opposite sides of the centre?
त्रिज्या 10 सेमी के एक वृत्त में, PQ और RS क्रमशः 16 सेमी और 12 सेमी लंबाई के दो समानांतर जीवा हैं। यदि वे केंद्र के विपरीत किनारों पर हैं, तो जीवा के बीच की दूरी कया है?
View SolutionTwo parallel chords of lengths 30cm and 16cm are drawn on the opposite sides of the centre of a circle of radius 17cm. Find the distance between the chords.
View Solution