PQRS is a cyclic quadrilateral. If angle P is three times the angle R and angle S is five times the angle Q , then the sum of angles Q and R is:
PQRS एक चक्रीय चतुर्भुज है | यदि कोण P कोण R का तिगुना है तथा कोण S कोण Q से पांच गुना है, तो कोण Q और R का योग ज्ञात करें |
65∘
70∘
75∘
72∘
To solve the problem, we need to find the sum of angles Q and R in the cyclic quadrilateral PQRS, given that angle P is three times angle R and angle S is five times angle Q.
1. Define Variables:
- Let angle R = α.
- Then angle P = 3α (since angle P is three times angle R).
- Let angle Q = β.
- Then angle S = 5β (since angle S is five times angle Q).
2. Use the Property of Cyclic Quadrilaterals:
- In a cyclic quadrilateral, the sum of opposite angles is 180 degrees:
Angle P+Angle R=180andAngle Q+Angle S=180
- Therefore, we can write:
3α+α=180(1)
β+5β=180(2)
3. Solve Equation (1):
- From equation (1):
4α=180
α=1804=45 degrees
4. Solve Equation (2):
- From equation (2):
6β=180
β=1806=30 degrees
5. Find the Sum of Angles Q and R:
- Now we have:
- Angle Q = β = 30 degrees
- Angle R = α = 45 degrees
- Therefore, the sum of angles Q and R is:
Q+R=β+α=30+45=75 degrees
Final Answer:
The sum of angles Q and R is 75 degrees.
---
- Let angle R = α.
- Then angle P = 3α (since angle P is three times angle R).
- Let angle Q = β.
- Then angle S = 5β (since angle S is five times angle Q).
- In a cyclic quadrilateral, the sum of opposite angles is 180 degrees:
Angle P+Angle R=180andAngle Q+Angle S=180
- Therefore, we can write:
3α+α=180(1)
β+5β=180(2)
- From equation (1):
4α=180
α=1804=45 degrees
- From equation (2):
6β=180
β=1806=30 degrees
- Now we have:
- Angle Q = β = 30 degrees
- Angle R = α = 45 degrees
- Therefore, the sum of angles Q and R is:
Q+R=β+α=30+45=75 degrees
The sum of angles Q and R is 75 degrees.
Topper's Solved these Questions
Similar Questions
PQRS is a cyclic quadrilateral. If angle P is four times the ∠R and ∠S is three times the ∠Q , then the sum of ∠Q and ∠R is:
PQRS एक चक्रीय चतुर्भुज है | यदि कोण P कोण R से चार गुना है तथा कोण S कोण Q से तीन गुना है, तो कोण Q और R का योग ज्ञात करें |
View SolutionPQRS is a cyclic quadrilateral. If ∠P is four times the ∠R and ∠S is three times the ∠Q , then the average of ∠Q and ∠R is:
PQRS एक चक्रीय चतुर्भुज है | यदि कोण P कोण R से चार गुना है तथा कोण S कोण Q से तीन गुना है, तो कोण Q और R का औसत ज्ञात करें |
View Solution
Knowledge Check
PQRs is a cyclic quadrilateral. Find the measure of ∠Pand∠Q.
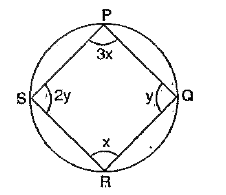 A135∘,60∘B60∘,120∘C60∘,90∘D100∘,120∘
A135∘,60∘B60∘,120∘C60∘,90∘D100∘,120∘In a parallelogram PQRS, angle P is four times of angle Q, then the measure of ∠R is
A144∘B36∘C72∘D130∘In ΔPQR, If ∠R>∠Q, then
AQR>PRBPQ>PRCPQ<PRDQR>PR
PQRS is a cyclic quadrilateral. If angle P is four times the ∠R and ∠S is three times the ∠Q , then the sum of ∠Q and ∠R is:
PQRS एक चक्रीय चतुर्भुज है | यदि कोण P कोण R से चार गुना है तथा कोण S कोण Q से तीन गुना है, तो कोण Q और R का योग ज्ञात करें |
View SolutionThe vertices A, B, C and D of a quadrilateral ABCD lie on a circle. ∠A is thrice ∠C and ∠D is twice ∠B. What is the difference between the measures of ∠B and ∠C?
किसी चतुर्भुज ABCD के शीर्ष बिंदु A, B, C और D एक वृत्त पर स्थित हैं | कोण A कोण C से तिगुना है तथा कोण D कोण B से दोगुना है | कोण B और कोण C के मान में क्या अंतर है ?
View SolutionS is the incentre of △PQR. If ∠PSR=125∘ , then the measure of ∠PQR is:
S, त्रिभुज PQR का अंतःकेंद्र है | यदि ∠PSR=125∘ है, तो कोण PQR का मान ज्ञात करें |
View SolutionABCD is a cyclic quadrilateral such that AB is the diameter of the circle circumscribing it and ∠ADC=129∘. Then ∠BAC is equal to:
ABCD एक ऐसा चक्रीय चतुर्भुज है कि AB इसे घेरने वाले वृत्त का व्यास है तथा ∠ADC=129∘ है | कोण BAC का मान ज्ञात करें |
View SolutionIn a quadrilateral PQRS, angle Q is twice the angle P. Angle R is thrice the angle P. The value of angle R is 150∘ What is the difference between angle Q and angle S?
View Solution
