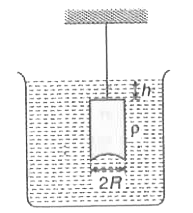
A hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is
 Solution in Gujrati
Solution in Gujrati
Mg
Mg−Vρg
Mg+πR2hρg
ρg(V+πR2h)
The correct Answer is:D
Step by step video & image solution for A hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density rho where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Multiple correct answers)
2 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Comprehension)
5 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 A (Previous year Questions)
29 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
A solid sphere of radius R and density ρ is attached to one end of a mass-less spring of force constant k. The other end of the spring is connected to another solid sphere of radius R and density 3ρ. The complete arrangement is placed in a liquid of density 2ρ and is allowed to reach equilibrium. The correct statements(s) is (are)
View SolutionA wooden cylinder of diameter 4 r, height H and density ρ/3 is kept on a hole of diameter 2 r of a tank, filled with water of density ρ as shown in the

If level of liquid starts decreasing slowly, when the level of liquid is at a height h1 above the cylinder, the block just start moving up. Then the value of h1 is
View SolutionA wire suspended vertically from one of itsends is strached by attached a weight of 200N to the lower end . The weight streches the wire by 1mm . Then the elastic energy stored in the wire is
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View SolutionA hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is

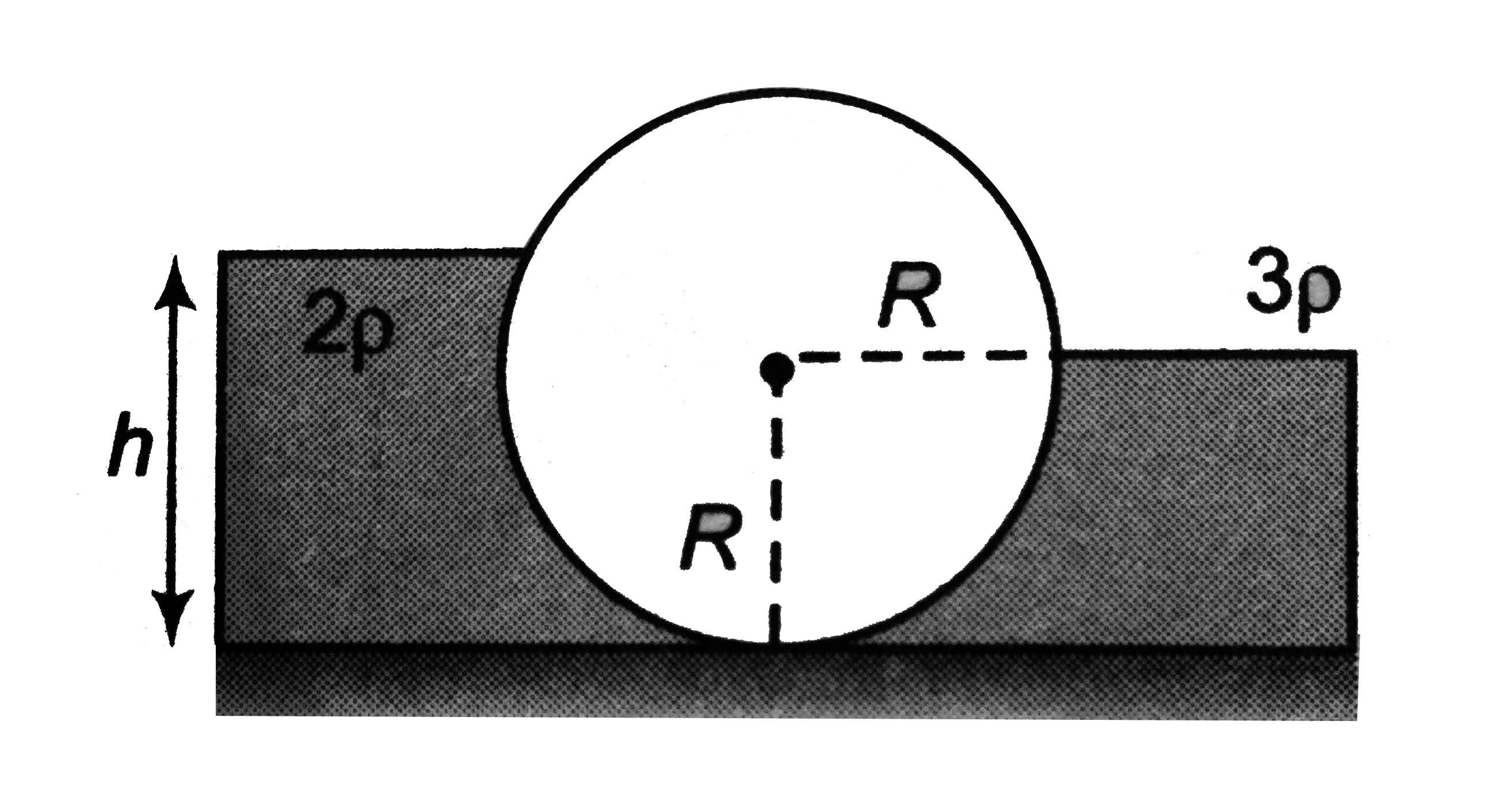
View SolutionIn the figure shown, the heavy cylinder (radius R) reasting on a smooth surface separates two liquids of densities 2ρ and 3ρ. The height h for the equilibrium of cylinder must be
View SolutionA hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder bby the liquid is

View Solution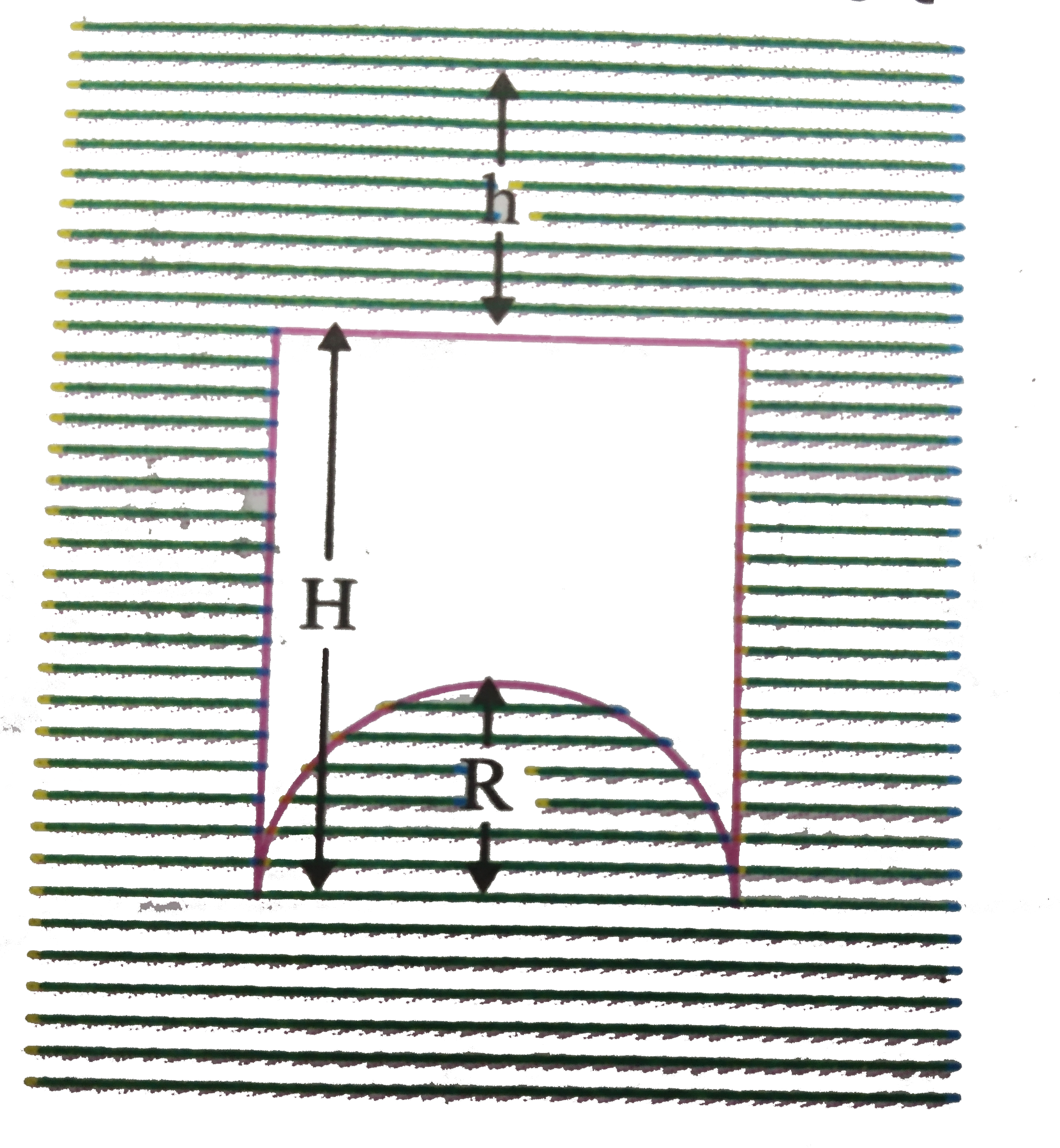
A cylinder of radius R, height H and density simga has a hemispherical cut at its bottom. The top of the cyliner is kept at depth h from the liquid surface. If the density of liquid is ρ, find the hydrostatic force acting on the hemispherical surface of the cylinder.
View SolutionA cylinder vessel containing a liquid of density rho is closed by a smooth piston of mass m as shown. If atmospheric pressure is P_0 , radius of cylinder is r and height of liquid is h . Find (a) Pressure of liquid just below the piston (b) force at bottom of cylinder. .
View SolutionA cylindrical vessel of radius r is filled with a homogeneous liquid upto a height h. It is found that the force exerted by the liquid column on the bottom of the cylinder is equal to the force exerted by the liquid on the sides of the cylinder. What is the relation between r and h?
View SolutionA conical portion of radius R and height H is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at depth h below the liquid surface . The force on the bottom of the cylinder by the liquid is

View SolutionR त्रिज्या के एक बेलन की तली से R त्रिज्या का ही अर्द्धगोलाकार भाग अलग कर दिया जाता है। शेष बचे बेलनाकार भाग का आयतन V तथा द्रव्यमान M है। इस भाग को एक डोरी द्वारा ऊर्ध्वाधर ρ' घनत्व वाले द्रव में लटका दिया जाता है। बेलन का ऊपरी सिरा द्रव के पृष्ठ से h गहराई पर है। द्रव द्वारा बेलन के निचले सिरे पर आरोपित बल है
View SolutionCalculate the moment of inertia of a hollow cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder?
View Solution
