In the figure shown, a particle P strikes the inclined smooth plane horizontally and rebounds vertically. If the angle θ is 60∘ then the coefficient of restitution is:
 Solution in Gujrati
Solution in Gujrati
1√3
2√3
13
None of these
The correct Answer is:C
Aong tangent
ucosθ=vsinθ …(i)
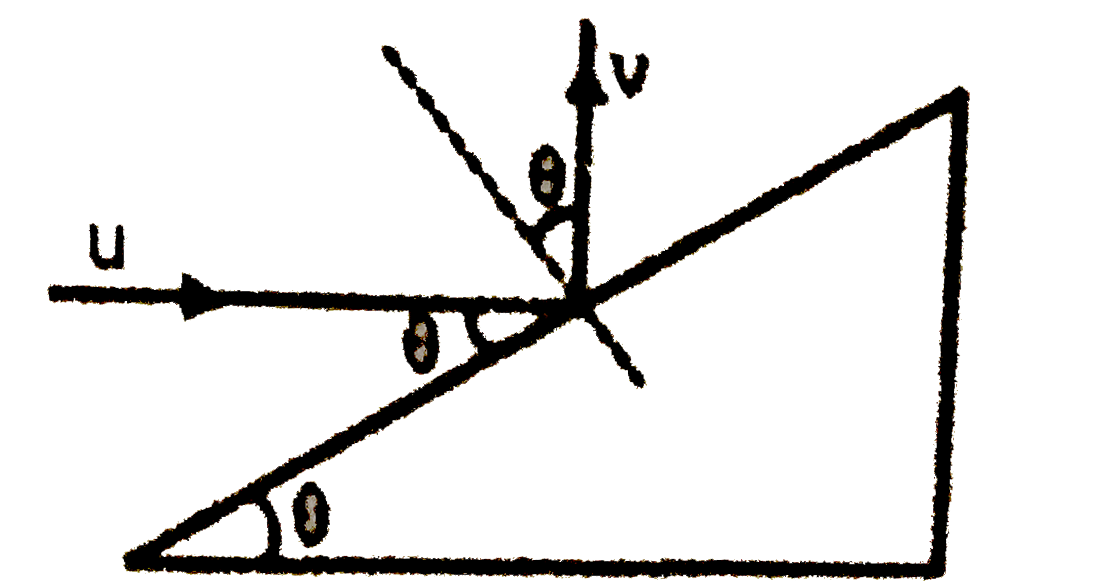
Along normal
e=vcosθusinθ=cot2θ=cot260=13
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III
41 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Two particle A and B start moving due to their mutual interaction only. If at any tiem 't', →aA and →aB are their respective accelerations, →vA and →vB are their respective velocities, and upto that time WA and WB are the work done on A and B respectively by the mutual force, mA and mB are their masses respectively, then which of the following is alwys correct.
View SolutionA particle of mass m, kinetic energy K and momentum p collision head on elastically with another particle of mass 2m at rest. After collision. :
Column IColumn II(A)Momentum of first particle(p)3/4p(B)Momentum of second particle(q)−K/9(C)Kinetic energy of first particle(r)−p/3(D)Kinetic energy of second particle(s)8K9None
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View SolutionAssertion: If the initial and final positions coincide, the displacement is a null vector.
Reason: A physical quantity can not be called a vector, if its magnitude is zero.
View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
View SolutionA particle of mass m strikes a horizontal smooth floor with velocity u making an angle theta with the floor and rebound with velocity v making an angle theta with the floor. The coefficient of restitution between the particle and the floor is e . Then
View SolutionA ball is projected in a direction inclined to the vertical and bounces on a smooth horizontal plane. The range of one rebound is R . If the coefficient of restitution is e , then range of the next rebound is
View SolutionA particle strikes a horizontal smooth floor with a velocity a making an angle θ with the floor and rebounds with velocity v making an angle ϕ with the floor. If the coefficient of restitution between the particle and the floor is e, then
View SolutionA particle is to be projected horizontally with velocity v from a point P , which is 60 m above the foot of a plane inclined at angle 45^(@) with horizontal as shown in figure. The particle hits the plane perpendicularly at A . After rebound from inlined plane it again hits at B . If coefficient of restitution between particles and plane is (1)/(sqrt(2)) then,
View SolutionA particle strikes a smooth horizontal surface at an angle of 45^(@) with a velocity of 100m//s and rebounds. If the coefficient of restitution between the floor and the particle is 0.57 then the angle which the velocity of the particle after it rebounds will make with the floor is
View SolutionA particle strikes a horizontal frictionless floor with a speed u, at an angle theta with the vertical, and rebounds with a speed upsilon , at an angle phi with the vertical. The coefficient of restitution between the particle and the floor is e. The angle phi is equal to :
View SolutionA particle strikes a horizontal frictionless floor with a speed u, at an angle θ to the vertical, and rebounds with a speed v, at an angle ϕ to the vertical. The coefficient of restitution between the particle and the floor is e. The magnitude of v is
View SolutionA particle strikes a smooth horizontal surface at an angle θ>0 and it rebounds at an angle ϕ as shown

View SolutionA particle strikes a horizontal smooth floor with a velocity u making an angle θ with the floor and rebounds with velocity v making an angle ϕ with the floor. The coefficient of restitution between the particle and the floor is e.
View SolutionA particle of mass m strikes a horizontal smooth floor with a velocity u making an angle 'θ' with the floor and rebound with velocity v making an angle 'ϕ' with the floor. The coefficient of restitution between the particle and the floor is e. Then
View SolutionA particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical, and rebounds with a speed v at an angle ϕ with vertical. The coefficient of restitution between the particle and floor is e. The magnitude of v is
View Solution
