A moving 2kg ball with a speed of 2ms−1 hits obliquely a stationary identical ball inelastically as shown. If the first ball move away with angle α=30∘ to the original path, find the total kinetic energy lost after the collision
 Solution in Gujrati
Solution in Gujrati
4/3J
5/4J
6/5J
7/6J
The correct Answer is:A

Tangential component remain same
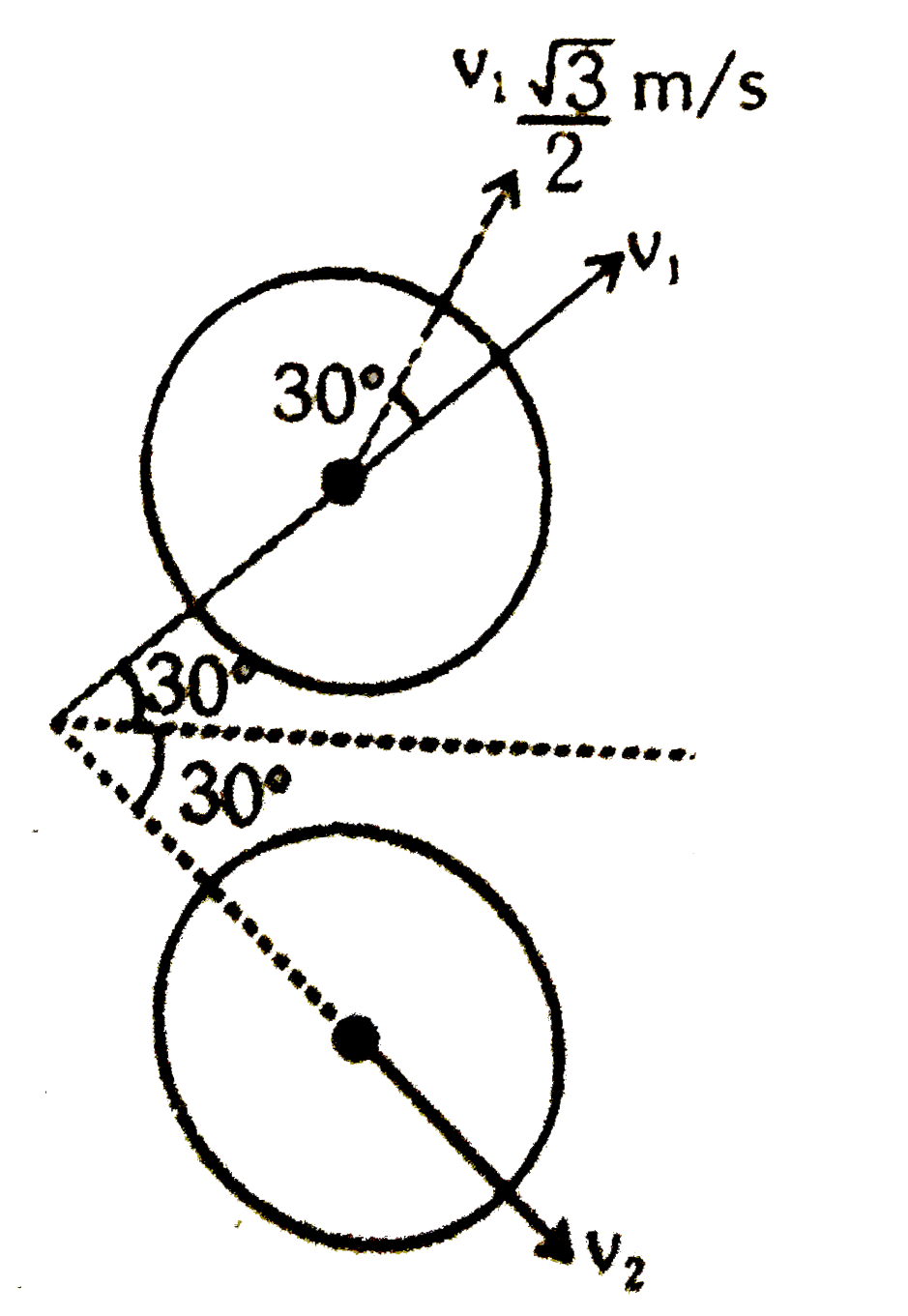
1=√3v12⇒v1=2√3
Momentum is conserved along normal
2√3=2×v12+2×v2⇒√3=1√3+v2
v2=2√3
ΔKE=12×2×4−⎛⎝12×2×(2√3)2+12×2×(2√3)2⎞⎠
=43J
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III
41 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Two particle A and B start moving due to their mutual interaction only. If at any tiem 't', →aA and →aB are their respective accelerations, →vA and →vB are their respective velocities, and upto that time WA and WB are the work done on A and B respectively by the mutual force, mA and mB are their masses respectively, then which of the following is alwys correct.
View SolutionA particle of mass m, kinetic energy K and momentum p collision head on elastically with another particle of mass 2m at rest. After collision. :
Column IColumn II(A)Momentum of first particle(p)3/4p(B)Momentum of second particle(q)−K/9(C)Kinetic energy of first particle(r)−p/3(D)Kinetic energy of second particle(s)8K9None
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View SolutionAssertion: If the initial and final positions coincide, the displacement is a null vector.
Reason: A physical quantity can not be called a vector, if its magnitude is zero.
View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
View SolutionA ball of mass m moving at a speed v makes a head on inelastic collision with an identical ball at rest. The kinetic energy of the balls after the collision is 3/4th of the original. Find the coefficient of restitution.
View SolutionA metal ball of mass 2 kg moving with speed of 36 Km//h has a collision with a stationary ball of mass 3 kg . If ater collision, both the ball move together, the loss in Kinetic energy due to collision is :
View SolutionA ball moving with a speed of 9m//s strikes an identical ball at rest, such that after the collision, the direction of each ball makes an angle of 30^(@) with the original line of motion. Find the speeds of the two balls after collision.
View SolutionA ball moving with a speed of 10" m s"^(-1) strikes an identical ball such that after the collision the direction of each ball makes an angle 45^(@) with the original line of motion. Find the speeds of the two balls after the collision.
View SolutionA ball of mass 1 kg moving with a velocity of "0.4 ms"^(-1) collides with another stationary ball. After the collision, the first ball moves with a velocity of 0.3ms^(1) in a direction making an angle of 90^(@) with its initial direction. The momentum of the second ball after the collision will be (in kg ms^(-1) )
View SolutionA ball moving with velocity of 6 m/s strikes an identical stationary ball. After collision each ball moves at an angle of 30^(@) with the original line of motion. What are the speeds of the balls after the collision ?
View SolutionA ball moving with a velocity 12m/s strikes an identical ball at rest.After collision both balls move in directions making 300 with original direction of motion.speeds of the balls after collision are (in ms−1) ?
View SolutionA ball moving with a speed of 9ms−1 strikes an identical ball such that after the collision the direction of each ball makes and angle 30∘ with the original line of motion. Find the speeds of the two balls after the collision.
View SolutionA ball moving with a velocity of 6 m/s strikes an identical stationary ball. After collisions each ball moves at an angle of 30^(@) with the original line of motion. What are the speeds of the balls after the collision?
View SolutionA ball moving with a velocity of 12ms−1 collides with another identical stationary ball . After the collision they move as shown in figure . Find the speed of the balls after the collision . Also , decide whether the condition is elastic or not .
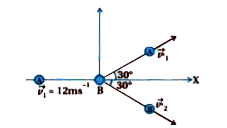
View SolutionA ball moving with a velocity of 6 m/s strikes an identical stationary ball. After collision each ball moves at angle of 30^@ with the original line of motion. Assuming that the collision is elastic, what are the speeds of the balls after the collision?
View Solution
