[Gujrati] A block of mass 0.9 kg attached to a spring of force constan

A mass M is performing linear simple harmonic motion. Then correct graph for acceleration a and corresponding linear velocity v is

View Solution

Column-I gives different situtions in which bodes are floating in liquid. Column-II gives correspoding time periods of oscillation.
ocr_image
A cube floating in liquid.

View Solution

A simple pendulum has time period $2 s$ . The point of suspension is now moved upward accoding to relation $y = (6 t - 3.75 t^{2}) m$ where $t$ is in second and y is the vertical displacement in upward direction. The new time period of simple pendulum will be

View Solution

The frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of

View Solution

Choose the correct statement:

View Solution

A block of mass $100 g$ attached to a spring ofstiffness $100 N / M i s$ lying on a frictionless floor as shown. The block is moved to compress the spring by $10 c m$ and released. If the collation with the wall is elastic then find the time period of oscillations.
ocr_image

View Solution

Figure shown a block P of mass m resting on a smooth horizontal surface, attached to a spring of force constant k which is rigidly fixed on the wall on left side, shown in the figure . At a distance l to the right of the block there is a rigid wall. If block is pushed towards loft so that spring is compressed by a distance $5 l / 3$ and when released, if will starts its oscillations. If collision of block with the wall is considered to be perfectly elastic. Find the time period of oscillation of the block.
ocr_image

View Solution

A block of mass $2 k g$ executes simple harmonic motion under the reading from at a spring .The angular and the time period of motion are $0.2 c m$ and $2 π$ sec respectively Find the maximum force execute by the spring in the block.

View Solution

A block of mass m moving at a speed v_0 compresses a spring of spring constant k as shown in the figure. Find (a) the maximum compression of spring and (b) speed of the block when the spring is compressed to half of maximum compression.

View Solution

A block is attached to a spring and is placed on a horizontal smooth surface as shown in which spring is unstretched. Now the spring is given an initial compression $2 x_{0}$ an block is released from rest. Collision with the wall $P Q$ are elastic.
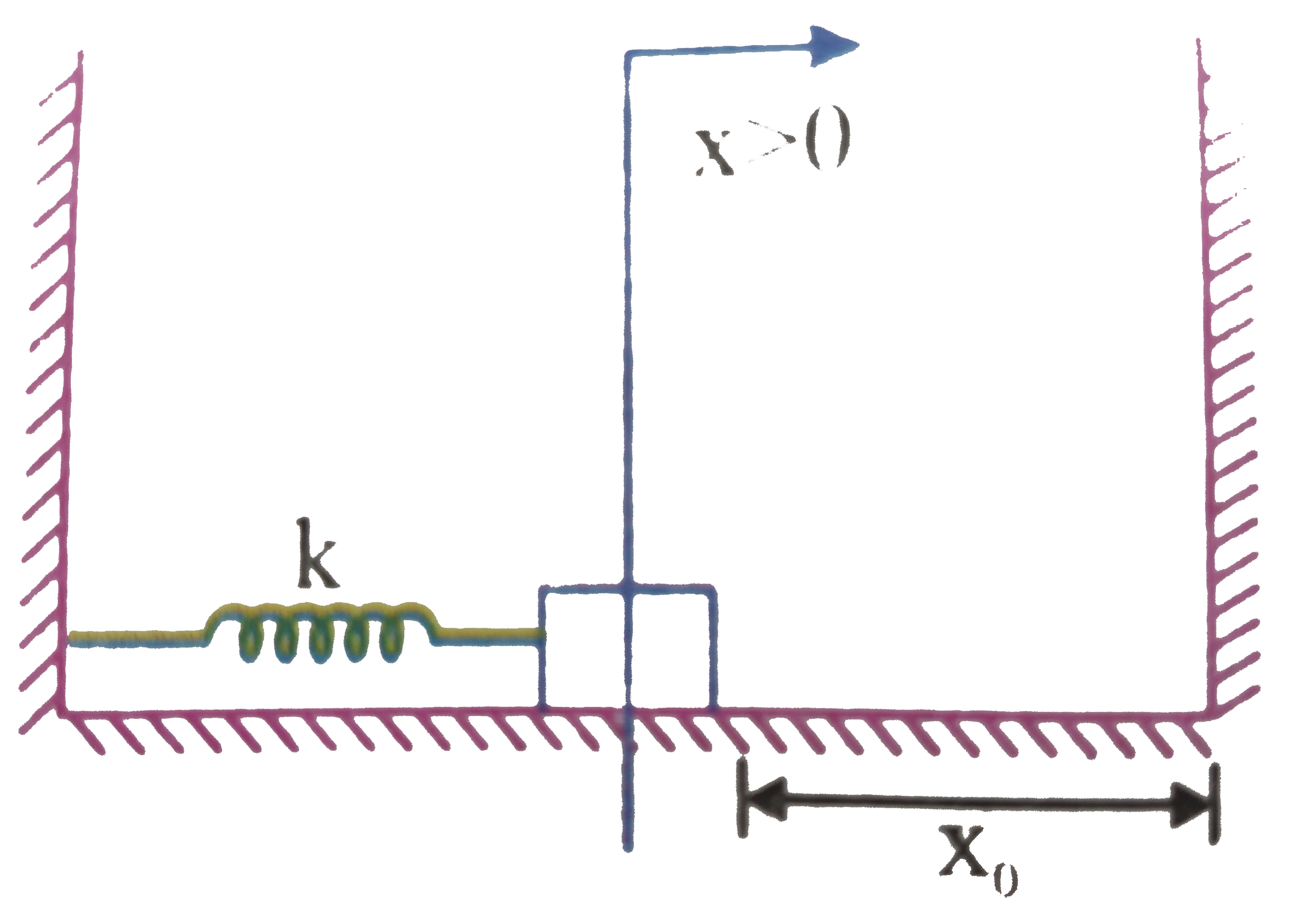
ocr_image
Find the time period of motion of the block:

View Solution

Initially spring is in its natural length . The block of mass 3 kg in contact with rigid wall . The block of mass 1 kg is pushed through a distance 4 cm towards the wall and then released. The velocity of the center of mass when the block of mass 3 kg breaks off the wall is (k = 100 N//m)

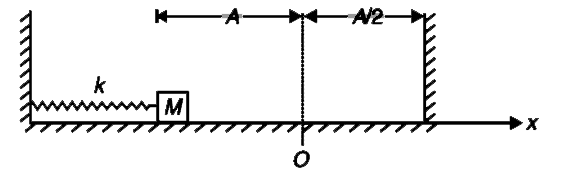
View Solution

A block of mass M connected to an ideal spring of force constant k, is placed on a smooth surface. The block is pushed to the left so as to compress the spring by a length A and then it is released. The block hits an elastic wall at a distance $\frac{3 A}{2}$ from its point of release. Assume the collision to be instantaneous.
(a) Calculate the time required by the block to complete one oscillation
(b) Draw the velocity - time graph for one oscillation of the block.
(c) Find the value of k for which average force experienced by the wall due to repeated hitting of the block is $F_{0}$ .
ocr_image

View Solution

In the figure, the block of mass m, attached to the spring of stiffness k is in correct with the completely elastic wall, and the compression in the spring is e. The spring is compressed further by e by displacing the block towards left and is then released. If the collision between the block and the wall is completely eleastic then the time period of oscillation of the block will be
ocr_image

View Solution

A block of mass m compresses a spring iof stifffness k through a distacne l//2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is

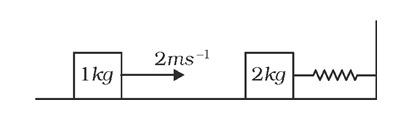
View Solution

A spring-block system is resting on a frictionless floor as shown in the figure. The spring constant is 2.0 N m^(–1) and the mass of the block is 2.0 kg. Ignore the mass of the spring. Initially the spring is in an unstretched condition. Another block of mass 1.0 kg moving with a speed of 2.0 m s^(–1) collides elastically with the first block. The collision is such that the 2.0 kg block does not hit the wall. The distance, in metres, between the two blocks when the spring returns to its unstretched position for the first time after the collision is _________.

View Solution

A spring-block system is resting on a frictionless floor as shown in the figure. The spring constant is $2.0 N m^{- 1}$ and the mass of the block is 2.0 kg. Ignore the mass of the spring. Initially the spring is in an unstretched condition. Another block of mass 1.0 kg moving with a speed of $2.0 m s^{- 1}$ collides elastically with the first block. The collision is such that the 2.0 kg block does not hit the wall. The distance, in metres, between the two blocks when the spring returns to its unstretched position for the first time after the collision is
ocr_image

View Solution

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

ALLEN -SIMPLE HARMONIC MOTION-Exercise-01