Block A in the figure is released from the rest when the extension in the spring is x0. The maximum downward displacement of the block will be :
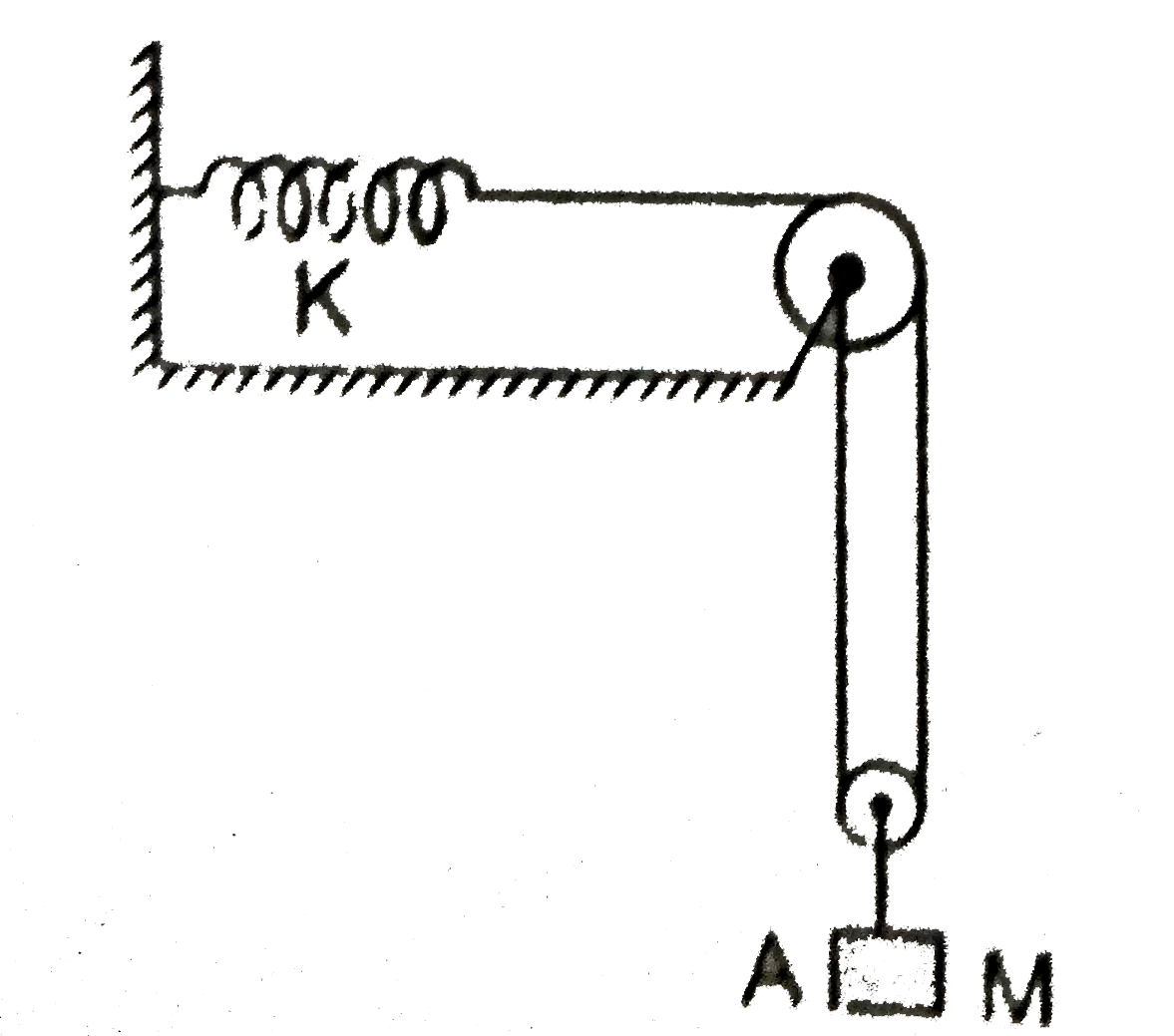Solution in Gujrati
Mg2k−x0
Mg2k+x0
2Mgk−x0
2Mgk+x0
The correct Answer is:A
For maximum displacement
Mg(x)=12k(2x)2⇒x=Mg2k⇒x=mg2k−x0
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-02
19 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise- 3 Match The Column
1 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - SOME WORKED OUT EXAMPLES
29 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
A mass M is performing linear simple harmonic motion. Then correct graph for acceleration a and corresponding linear velocity v is
View SolutionColumn-I gives different situtions in which bodes are floating in liquid. Column-II gives correspoding time periods of oscillation.
_E01_069_Q01.png)
A cube floating in liquid.
View SolutionA simple pendulum has time period 2s. The point of suspension is now moved upward accoding to relation y=(6t−3.75t2)m where t is in second and y is the vertical displacement in upward direction. The new time period of simple pendulum will be
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionChoose the correct statement:
View SolutionBlock A of the mass M in the figure is released from rest when the extension in the spring is x0. The maximum downwards displacement of the block is (assume x0<Mg/k).
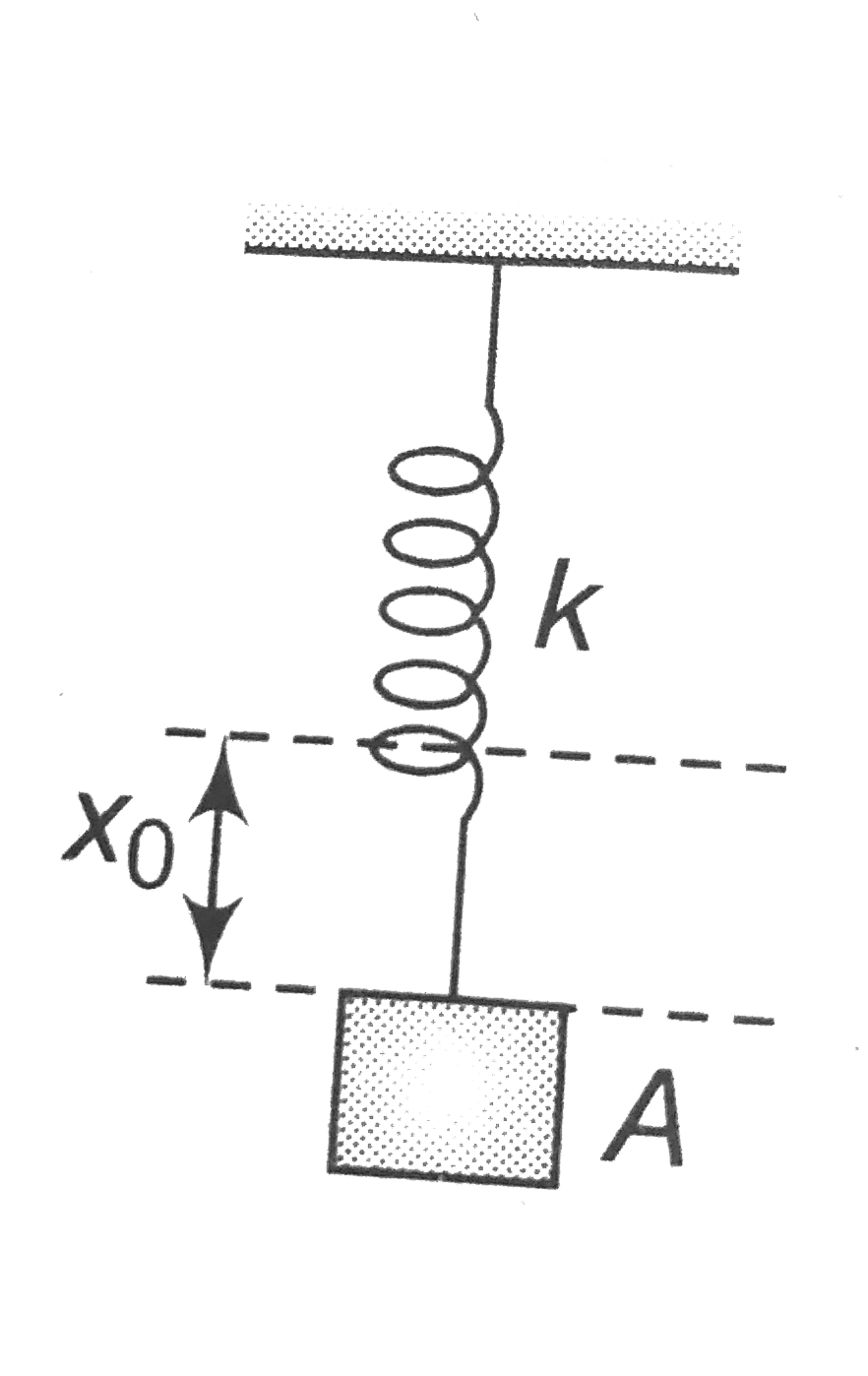
View SolutionThe given arrangement is released from rest when spring is in natural length. Maximum extension in spring during the motion is x_(0). a_(1),a_(2) and a_(3) are accelerations of the blocks. Make the correct options
View SolutionBlock A in the figure is released from rest when the extension in the spring is x0(x0<mg/k). The maximum downward displacement of the block is (there is no friction) :
View SolutionBlock A in the figure is released from the rest when the extension in the spring is x0. The maximum downward displacement of the block will be :
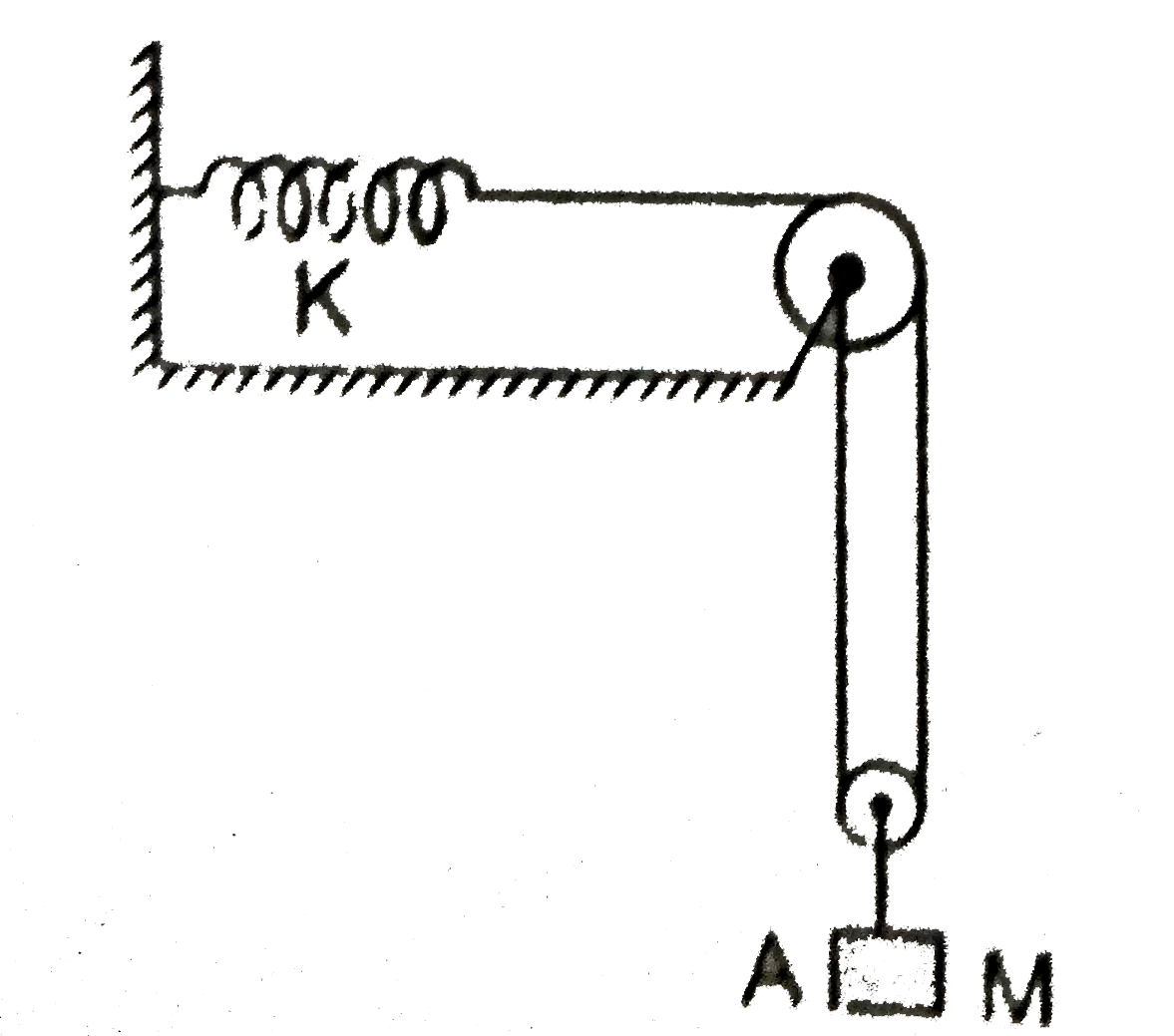
View SolutionA block is suspended by an ideal spring of force constant force F and if maximum displacement of block from its initial mean position of rest is x0 then
View SolutionBlocks A and B shown in the figure are having equal masses m. The system is released from rest with the spring unstretched. The string between A and ground is cut, when there is maximum extension in the spring. The acceleration of centre of mass of the two blocks at this instant is
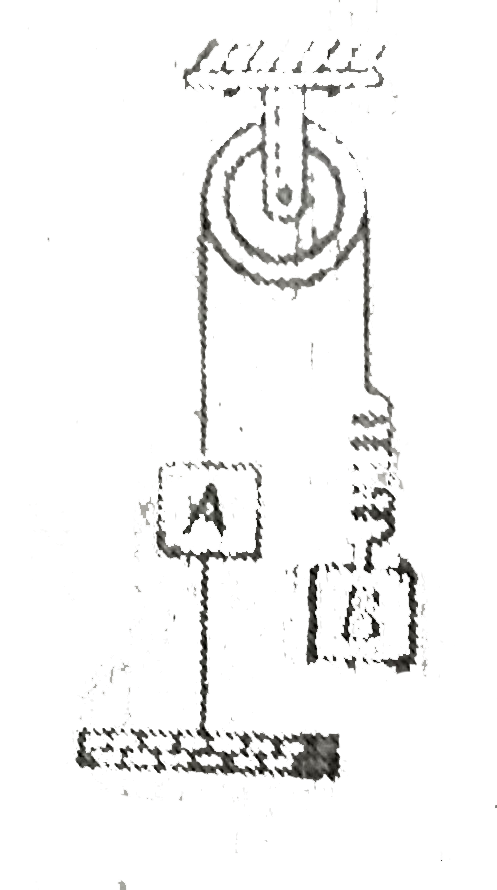
View SolutionConsider the situation shown in figure. Mass of block A is m and that of blcok B is 2m. The force constant of string is k. Friction is absent everywhere. System is released from rest with the spring unstretched. Find (a) The maximum extension of the spring x_(m) (b) The speed of block A when the extension in the springt is x=(x_(m))/(2) (c ) The net acceleration of block B when extension in the spring is x=(x_(m))/(4).
View SolutionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.
View SolutionThe block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m
View SolutionIn the situations shown in the figure surfaces are frictionless. Find the maximum extension of the springs if blocks are initially at rest and springs are initially in natural lengths.
View SolutionIn the adjoining figure, block A is of mass (m) and block B is of mass 2m. The spring has force constant k. All the surfaces are smooth and the system is released form rest with spring unstretched. Find the maximum extension in the spring and acceleration of block B at time of maximum extension .
View Solution