A mass M is in static equilibrium on a massless vertical spring as shown in the figure. A ball of mass m dropped from certain height sticks to the mass M after colliding with it.The oscillations they perform reach to height a above the original level of scales & depth 'b' below it.
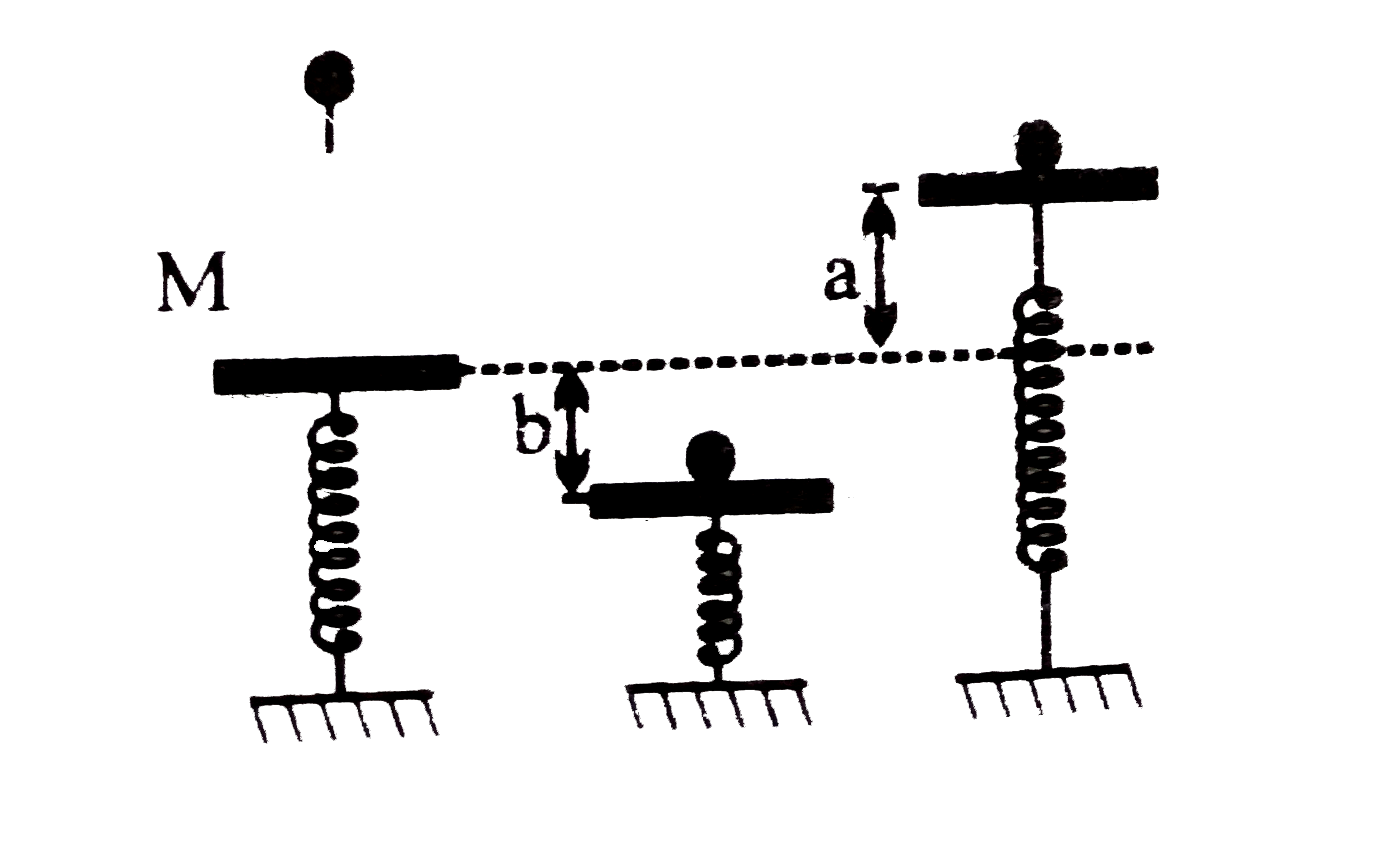
(a) Find the constant of force of the spring.,
(b) Find the oscillation frequency. Solution in Gujrati
The correct Answer is:A, B
(i) Let x0=Mgk = initial compression in spring
COME : 12k(x0+b)2=12k(a−x0)(2)+(m+M)g(b+a)
⇒k=2mgb−a
(ii) k=2mg(b−a)⇒(m+M)ω2=2mgb−a
⇒f=12π√2mg(b−a)(m+M)
(iii) Let h= initial height of m over the pan
v= common velocity of (m+M) after collision
COLM :m√(2gh)=(m+M)v......(i)
COME : 12kx02+12(m+M)v2+(m+M)gb=12k(x0+b)2
⇒=h=(M+mm)(abb−a)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [A]
39 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [B]
12 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-04 [A]
20 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
If a spring has time period T, and is cut into (n) equal parts, then the time period of each part will be.
View SolutionA particle of mass (m) is executing oscillations about the origin on the x axis. Its potential energy is V(x)=k|x|3 where k is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
View SolutionA particle simple harmonic motion completes 1200 oscillations per minute and passes through the mean position with a velocity 3.14ms−1. Determine displacement of the particle from its mean position. Also obtain the displacement equation of the particle if its displacement be zero at the instant t=0.
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionChoose the correct statement:
View SolutionA block of mass m is dropped onto a spring of constant k from a height h . The second end of the spring is attached to a second block of mass M as shown in figure. Find the minimum value of h so that the block M bounces off the ground. If the block of mass m sticks to the spring immediately after it comes into contact with it.
View SolutionA mass M is in static equilibrium on a massless vertical spring as shown in the figure. A ball of mass m dropped from certain height sticks to the mass M after colliding with it.
The oscillations they perform reach to height'a' above the original level of scales & depth 'b' below it.
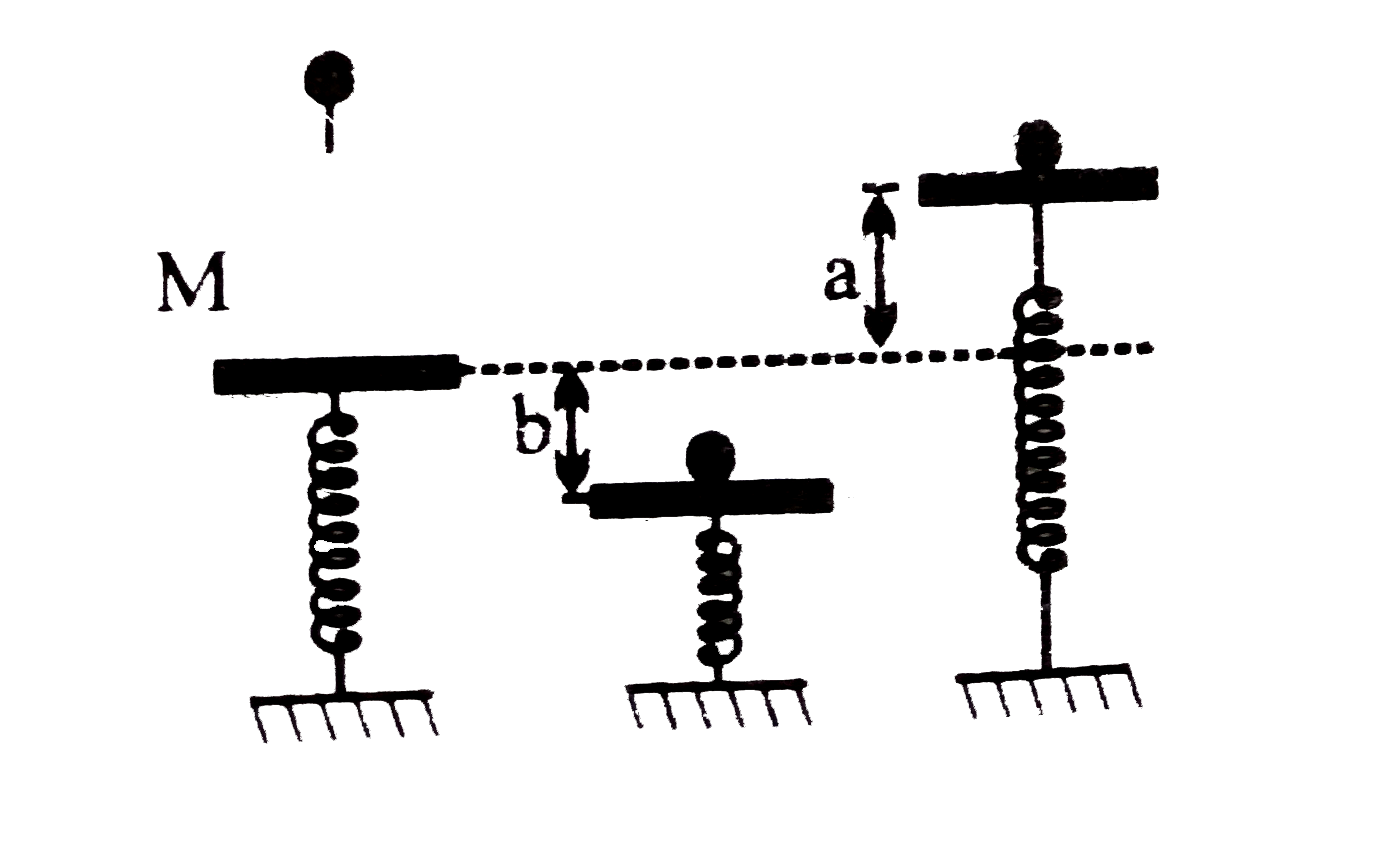
(a) Find the constant of force of the spring.,
(b) Find the oscillation frequency.
(c ) What is the height above the initial level from which the mass m was dropped?
View SolutionA body of mass m falls from a height h onto the pan of a spring balance. The masses of the pan and spring are negligible. The force constant of the spring is k. The body sticks to the pan and oscillates simple harmonically. The amplitude of oscillation is

View SolutionA solid ball of mass m is made to fail from a height H on a pan suspended through a spring of spring constant K as shown in figure. If the does not rebound and the pan is massless, then amplitude of oscillation is
View SolutionAn ideal spring supports a disc of mass M. A body of mass m is released from a certain height from where it falls to hit M. The two masses stick together at the moment they touch and move together from then on . The oscillations reach to a height a above the original level of the disc and depth b blow. it The constant of the force of the spring is
View SolutionA mass m = 50 g is dropped on a vertical spring of spring constant 500 N/m from a height h= 10 cm as shown in figure (18-E14). The mass sticks to the spring and executes simple harmonic oscillations after that. A concave mirror of focal length 12 cm facing the mass is fixed with its principal axis coinciding with the line of motion of the mass, its pole being at a distance of 30 cm from the free end of the spring. Find the length in which the image of the mass oscillates.
View SolutionAn ideal spring supports a disc of mass M. A body of mass m is released from a certain height from where it falls to hit M. The two masses stick together at the moment they touch and move together from then on. The oscillations reach to a height a above the original level of the disc and depth b below it. The constant of the force of the spring is
View SolutionA particle of mass 'm' is attached to three identical springs A, B and C each of force constant 'k' as shown in figure. If the particle of mass 'm' is pushed sightly against the spring 'A' and released. Find the period of oscillation
View SolutionA particle of mass 'm' is attached to three identical springs A, B and C each of force constant 'k' as shown in figure. If the particle of mass 'm' is pushed sightly against the spring 'A' and released. Find the period of oscillation
View SolutionA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

View Solutionएक m द्रव्यमान का गुटका स्प्रिंग नियतांक k की स्प्रिंग से ऊर्ध्वाधर रूप से लटक रहा है। यदि द्रव्यमान को ऊर्ध्वाधर रूप से दोलन कराया जाता है, तो इसकी कुल ऊर्जा होती है
View Solution
