Two independent harmonic oscillators of equal mass are oscillating about the origin with angular frequencies (omega_1) and (omega_2) and have total energies (E_1 and E_2), respectively. The variations of their momenta (p) with positions (x) are shown (s) is (are) a/b = n(square) and a/R= n, then the correct eqution......
(##JMA_CHMO_C10_022_Q01##)Solution in Gujrati
E1ω1=E2ω2
ω2ω1=n2
ω1ω2=n2
E1ω1=E2ω2
The correct Answer is:B, D
P1max=maω1=b
P2max=mRω2=R
ω1ω2=1n2
ω2ω1=n2
E1=12mω21a2
E2=12mω22R2
E1E2=ω21ω22a2R2=ω21ω22n2=ω21ω22ω2ω1
E1E2=ω1ω2
E1E2=E2ω2
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Paragraph
3 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Subjective
30 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [B]
12 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
A uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.
The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.
View SolutionTwo masses m1 and m2 concute a high spring of natural length l0 is compressed completely and tied by a string. This system while conving with a velocity v0 along +ve x-axis pass thorugh the origin at t=0, at this position the string sanps, Position of mass m1 at time t is given by the equation x1t=v0(A/1−cosωt). Calculate (i) position of the particle m2 as a funcation of time, (ii) l0 in terms of A.
View SolutionA particle of mass (m) is executing oscillations about the origin on the x axis. Its potential energy is V(x)=k|x|3 where k is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionChoose the correct statement:
View SolutionTwo bodies with moment of inertia I1 and I2(I1>I2) have equal angular momenta. If their kinetic energy of rotation are E1 and E2 respectively, then.
View SolutionWhen a particle oscillates simple harmonically, its potential energy varies periodically. If the frequency of oscillation of the particle is n, the frequency of potential energy variation is
View SolutionTwo independent harmonic oscillators of equal mass are oscillating about the origin with angular frequencies omega_(1) and omega_(2) and have total energies E_(1) and E_(2) repsectively. The variations of their momenta p with positions x are shown in figures. If (a)/(b) = n^(2) and (a)/(R) = n , then the correc t equation(s) is (are) :
View Solutionदो स्वतंत्र समान द्रव्यमान के आवर्त दोलन मूल बिन्दु से परितः कोणीय आवृत्तियों ω1 , एवं ω2 , तथा कुल ऊर्जाओं क्रमश: E1, तथा E2 से दोलन कर रहे हैं। उनके संवेगों (p) का स्थिति x के साथ परिवर्तन सम्बन्ध चित्रों में दर्शाये गये हैं। यदि ab = n2 तथा aR=n है, तब सही कथन है
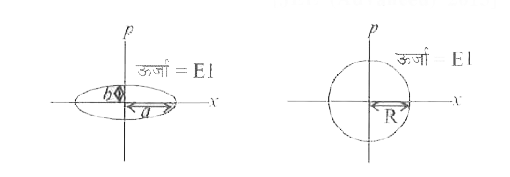
View SolutionThe variations of potential energy (U) with position x for three simple harmonic oscillators A, B and C are shown in figure. The oscillators have same mass. The time period of oscillation is greatest for
View Solutionसमष्टि S में किन्हीं दो स्वतन्त्र घटनाओं E1 तथा E2के लिए P[(E1∪E2)∩(E1∩E2)] का मान है
View SolutionWhen a particle oscillates simple harmonically, its potential energy varies periodically. If the frequency of oscillation of the particle is n, the frequency of potential energy variation is………………
View SolutionWhen a particle oscillates simple harmonically, its potential energy varies periodically. If the frequency of oscillation of the particle is n, the frequency of potential energy variation is………………
View SolutionWhen a particle oscillates simple harmonically, its potential energy varies periodically. If the frequency of oscillation of the particle is n, the frequency of potential energy variation is………………
View SolutionIn force oscillation of a particle, the amplitude is maximum for a frequency omega_1 , while the energy maximum for a frequency omega_2 , of the force. Then
View SolutionFor a simple harmonic oscillator the frequency of oscillation is independent of
View Solution
