A block with mass (M) is connected by a massless spring with stiffness constant (k) to a rigid wall and moves without friction on a horizontal surface. The block oscillates with small amplitude A about an equilibrium position (x_0). Consider two cases : (i) when the block is at (x_0) , and (ii) when the block is at x=x0+A. In both the cases, a particle with mass m(lt M) is softly placed on the block after which they strick to each other. Which of the following statement (s) is (are) true about the motion after the mass (m) is placed on the mass (M) ?Solution in Gujrati
The amplitude of oscillation in the first case changes by a factor of √Mm+M, whereas in the second case it remains unchanged
The final time period of oscillation in both the cases in same
The total energy decreases in both the cases
The instantaneous speed at x0 at the combined decreases in both the cases.
The correct Answer is:A, B, D
Ti=2π√MK,Tf=2π√M+mK
case (i):M(Aω)=(M+m)V
∴ Velocity decreases at equilibrium position.
By energy conservation
Af=Ai√MM+m
case (ii) :
No energy loss, amplitude remains same
At equilibrium (x0) velocity =Aω
In both cases ω decreases so velocity decreases in both cases
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Paragraph
3 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Subjective
30 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [B]
12 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
A uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.
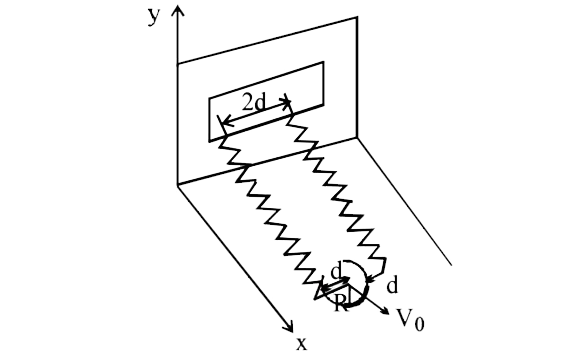
The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.
View SolutionTwo masses m1 and m2 concute a high spring of natural length l0 is compressed completely and tied by a string. This system while conving with a velocity v0 along +ve x-axis pass thorugh the origin at t=0, at this position the string sanps, Position of mass m1 at time t is given by the equation x1t=v0(A/1−cosωt). Calculate (i) position of the particle m2 as a funcation of time, (ii) l0 in terms of A.
View SolutionA particle of mass (m) is executing oscillations about the origin on the x axis. Its potential energy is V(x)=k|x|3 where k is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionChoose the correct statement:
View SolutionA block P of mass m is placed on horizontal frictionless plane. A second block of same mass m is placed on it and is connected to a spring of spring constant k, the two blocks are pulled by distance A. Block Q oscillates without slipping. What is the maximum value of frictional force between the two blocks.

View SolutionTwo spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is
View Solution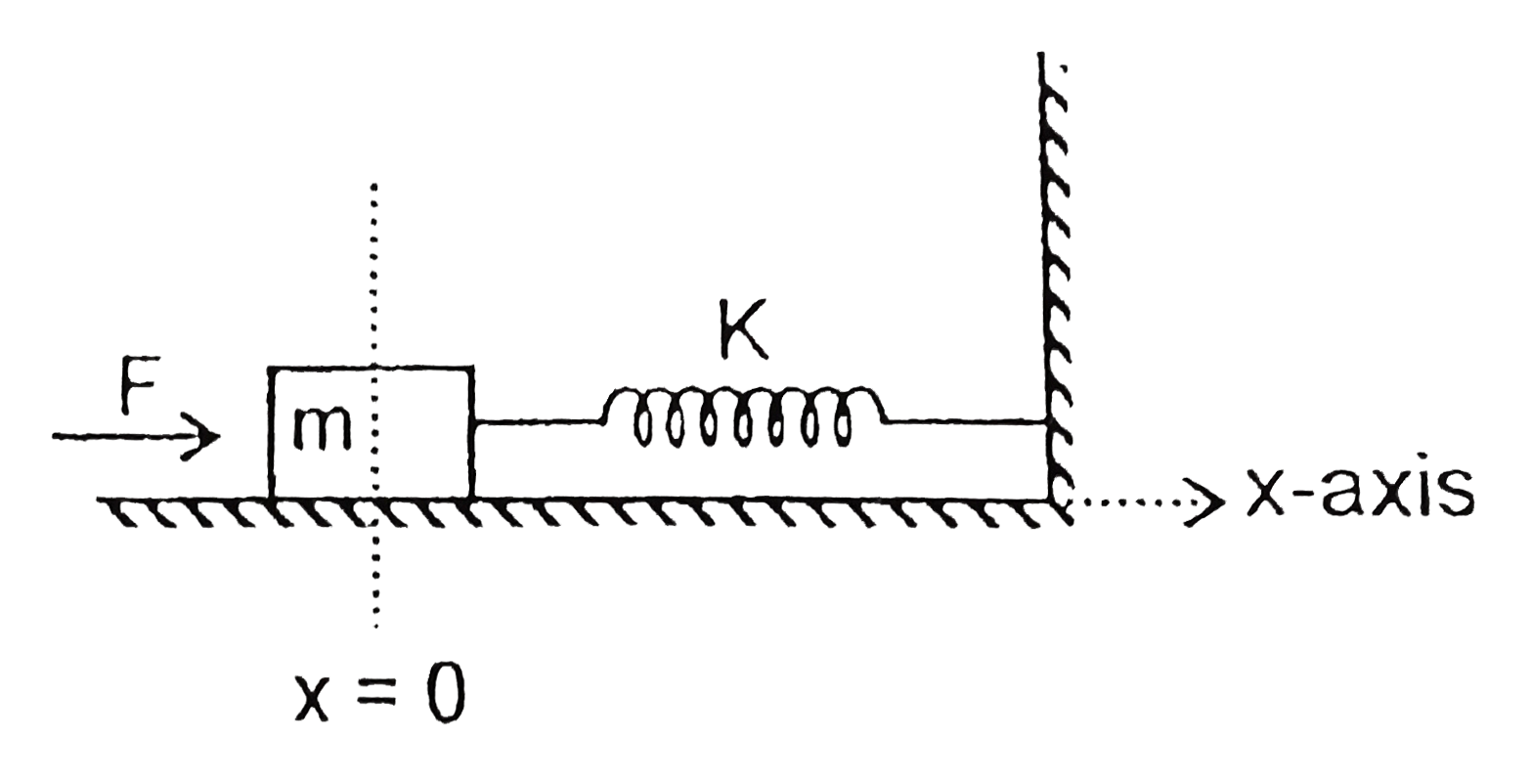
A block of mass m connected to a spring of stiffness k is placed on horizontal smooth surface. When block is at x=0, spring is in natural length. The block is also subjected to a force F=k|x|∘ then
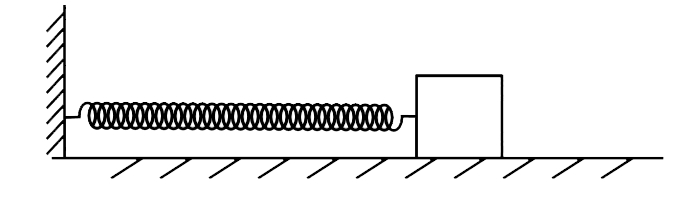
View SolutionA spring block system is placed on a rough horizontal floor. Force constant of the spring is k. The block is pulled to right to give the spring an elongation equal to x0 and then it is released. The block moves to left and stops at the position where the spring is relaxed. Calculate the maximum kinetic energy of the block during its motion.
View SolutionA block Q of mass 2m is placed on a horizontal frictionless plane. A second block of mass m is placed on it and is connected to a spring of spring constant K, the two block are pulled by distance A. Block Q oscillates without slipping. The work done by the friction force on block Q when the spring regains its natural length is:
View Solutionm द्रव्यमान का एक ब्लॉक P क्षैतिज चिकने समतल पर रखा है। समान द्रव्यमान m का एक दूसरा ब्लॉक Q इस पर रखा है तथा स्प्रिंग नियतांक k की एक स्प्रिंग से जुड़ा है। दोनों ब्लॉक दूरी A से विस्थापित किए जाते हैं। ब्लॉक Q बिना फिसले दोलन करता है। दोनों ब्लॉकों के मध्य घर्षण बल का अधिकतम मान है
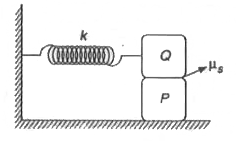
View SolutionA block Q of mass 2m is placed on a horizontal frictionless plane. A second block of mass m is placed on it and is connected to a spring of spring constant K, the two block are pulled by distance A. Block Q oscillates without slipping. The work done by the friction force on block Q when the spring regains its natural length is
View Solutionएक ब्लॉक चित्रानुसार एक स्प्रिंग से सम्बद्ध है। स्प्रिंग नियतांक k व अल्प घर्षण बल f है। यदि ब्लॉक को साम्यावस्था से x0 दूरी खींच कर छोड़ दिया जाये तो ये कुछ समय तक दोलन के उपरान्त स्थिर हो जाता है। दोलन में अवमन्दन का कारण घर्षण है।

विराम अवस्था में आने से पहले ब्लॉक कितने दोलन पूर्ण कर लेगा ?
View SolutionA block diagram is associated with a spring. The spring constant k and the small friction force are f. If the block is out of sync x_0 If the distance is dragged and left, it becomes stable after oscillation for some time. The reason for damping in oscillation is friction. The total distance traveled by the block from start to finish will be
View Solutionद्रव्यमान m की एक वस्तु स्प्रिंग स्थिरांक k के द्रव्यमान रहित स्प्रिंग के एक सिरे से जुड़ी होती है। स्प्रिंग का दूसरा सिरा एक दीवार से सटा हुआ है। ब्लॉक एक क्षैतिज खुरदरी सतह पर चल सकता है। ब्लॉक और सतह के बीच घर्षण का गुणांक है μ । तब स्प्रिंग का संपीड़न जिसके लिए स्प्रिंग का अधिकतम विस्तार अधिकतम संपीड़न का आधा हो जाता है:
View SolutionTwo springs are connected to a block of mass M is placed on a frictionless surface as shown in figure. If both springs have a spring constant k, the frequency of oscillation of the block is………

View Solution
