[Gujrati] Young's modulus of brass and steel are 10 xx 10^(10) N//m^(2

Blood is flowing at the rates of 200 $c m^{3} / sec$ in a capillary of cross-sectional area $0.5 m^{2}$ . The velocity of flow, (in mm/sec) is:

View Solution

A tank 5 m high is half filled with water and then is filled to top with oil of density $0.85 g / c m^{3}$ The pressure at the bottom of the tank, due to these liquids is

View Solution

Two paricles of equal mass $m$ go round a circle of radius R under the action of their mutual gravitional attraction. The speed of each particle is

View Solution

Assertion: The driver in a vechicle moving with a constant speed on a straight road is in a non-inertial frame of referance.
Reason: A reference frame in which Newton's laws of motion are applicable is non-inertial.

View Solution

A rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be

View Solution

Two wires of diameter 0.25 cm , one made of steel and other made of brass, are loaded as shown in the figure. The unloaded length of the steel wire is 1.5 m and that of brass is 1.0 m . Young's modulus of steel is 2.0 xx 10^(11) Pa and that of brass is 1.0 xx 10^(11) Pa. Compute the ratio of elongations of steel and brass wires. (/_\l_("steel"))/(/_\l_("brass"))=?

View Solution

Young's modulus of brass and steel are $10 \times 10^{10} N / m$ and $2 \times 10^{11} N / m^{2}$ , respectively. A brass wire and a steel wire of the same length are extended by $1 m m$ under the same force. The radii of the brass and steel wires are $R_{B}$ and $R_{S}$ . respectively. Then

View Solution

The young 's modulus of brass and steel are 1.0 xx 10^(11) Nm^(-2) and 2.0 xx 10^(11) N//m^(2) . Respectively . A brass wire and steel wire of the same length extend by 1 mm, each under the same forece . It radii of brass and steel wires are R_(B) and R_(S) respectively, them

View Solution

The Young's modulus of brass and steel are respectively $1.0 \times 10^{11} N / m^{2}$ and $2.0 \times 10^{11} N / m^{2}$ . A brass wire and steel wire of the same length are extended by $1 m m$ each under the same force. If radii of brass and steel wires are $R_{B}$ and $R_{S}$ respectively,. then

View Solution

The Young's modulus of brass and steel are respectively $1.0 \times 10^{11} N m^{- 2}$ and $2.0 \times 10^{11} N m^{- 2}$ . A brass wire and a steel wire of the same length are extended by 1 mm each under the same force. If radii of bras and steel wires are $R_{B}$ and $R_{s}$ respectively, then

View Solution

If a uniform brass wire of length 5 m and radius $10^{- 3}$ m is extended by $10^{- 3}$ m, then the energy stored in the wire will be
(Young's modulus for brass $= 10 \times 10^{10} N / m^{2}$ )

View Solution

The Young's modulii of brass ans steel are in the ratio of $1 : 2$ . A brass wire and a steel wire of the same length are extended by the same amount under the same deforming force. If $r_{B}$ and $r_{S}$ are the radii of brass and steel wires respectively, then

View Solution

Two wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in figure. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires .Young's modulus of steel is $2.0 \times 10^{11}$ Pa and that of brass is $9.1 \times 10^{11}$ Pa.
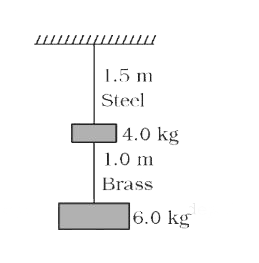
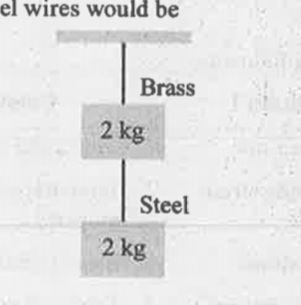
ocr_image

View Solution

If the ratio of lengths, radii and Young's modulus of steel and brass wires shown in the figure are a, b and c respectively, the ratio between the increase in lengths of brass and steel wires would be Brass and steel wire would be
ocr_image

View Solution

The Young's Modulus of steel is twice that of brass. Two wires of same length and of same area of cross-section, one of steel and another of brass are suspended from the same roof. If then the weights added to the steel and brass wires must be in the ratio of

View Solution

The ratios of length areas of cross-section and Young's modulii of steel of that of brass wires shown in the figure are a,b and c respectively . The ratio of increase in the lengths of brass of that of steel wires is [Assume that the masses of steel and brass wires are negligible]

View Solution

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

ALLEN -RACE-Basic Maths (Properties of Matter & Fluid Mechanics)(Elasticity)

Young's modulus of brass and steel are 10×1010N/m2 and 2×1011N/m2, respectively. A brass wire and a steel wire of the same length are extended by 1mm under the same force. The radii of the brass and steel wires are RB and RS respectively. Then Solution in Gujrati

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

ALLEN -RACE-Basic Maths (Properties of Matter & Fluid Mechanics)(Elasticity)