A horizontal platform is rotating with uniform angular velcity around the vertical axis passing through its centre. At some instant of time a viscous fluid of mass m is dropped at the centre and is allowed to spread out and finally fall. The angular velocity during this period :
decreases continuously
decreases initially and increases again
remains unaltered
increases continuously
The correct Answer is:B
To solve the problem, we need to analyze the situation using the principles of angular momentum and the effects of adding mass to a rotating system.
1. Understanding the System:
- We have a horizontal platform rotating with a uniform angular velocity (ω) around a vertical axis.
- At a certain moment, a viscous fluid of mass 'm' is dropped at the center of the platform.
2. Moment of Inertia:
- The moment of inertia (I) of the system will change when the fluid is added. Initially, the moment of inertia is I₀ (the moment of inertia of the platform alone).
- When the fluid is added and spreads out, the total moment of inertia increases because the fluid has mass and it contributes to the overall distribution of mass in the system.
3. Conservation of Angular Momentum:
- According to the conservation of angular momentum, the initial angular momentum (L₀) of the system must equal the final angular momentum (L) after the fluid is added.
- Mathematically, this can be expressed as:
I₀⋅ω=I⋅ω′
where ω' is the new angular velocity after the fluid is added.
4. Effect of Increasing Moment of Inertia:
- Since the moment of inertia (I) increases due to the addition of the fluid, and angular momentum is conserved, we can see that:
I₀⋅ω=I⋅ω′
implies that if I increases, ω' must decrease to keep the equation balanced.
5. Final Behavior of Angular Velocity:
- Initially, as the fluid spreads out, the moment of inertia increases, causing the angular velocity to decrease.
- After the fluid has spread out and starts to fall, the moment of inertia may decrease (as the mass is no longer contributing to the rotation), which could lead to an increase in angular velocity.
- Therefore, we can conclude that the angular velocity decreases initially and then may increase again after the fluid has settled.
Conclusion:
The correct answer is that the angular velocity decreases initially and then increases again.
- We have a horizontal platform rotating with a uniform angular velocity (ω) around a vertical axis.
- At a certain moment, a viscous fluid of mass 'm' is dropped at the center of the platform.
- The moment of inertia (I) of the system will change when the fluid is added. Initially, the moment of inertia is I₀ (the moment of inertia of the platform alone).
- When the fluid is added and spreads out, the total moment of inertia increases because the fluid has mass and it contributes to the overall distribution of mass in the system.
- According to the conservation of angular momentum, the initial angular momentum (L₀) of the system must equal the final angular momentum (L) after the fluid is added.
- Mathematically, this can be expressed as:
I₀⋅ω=I⋅ω′
where ω' is the new angular velocity after the fluid is added.
- Since the moment of inertia (I) increases due to the addition of the fluid, and angular momentum is conserved, we can see that:
I₀⋅ω=I⋅ω′
implies that if I increases, ω' must decrease to keep the equation balanced.
- Initially, as the fluid spreads out, the moment of inertia increases, causing the angular velocity to decrease.
- After the fluid has spread out and starts to fall, the moment of inertia may decrease (as the mass is no longer contributing to the rotation), which could lead to an increase in angular velocity.
- Therefore, we can conclude that the angular velocity decreases initially and then may increase again after the fluid has settled.
The correct answer is that the angular velocity decreases initially and then increases again.
Similar Questions
A horizontal disk is rotating with angular velocity ω about a vertical axis passing through its centre. A ball is placed at the centre of groove and pushed slightly. The velocity of the ball when it comes out of the groove -

View SolutionA horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View SolutionA uniform disk of mass 300kg is rotating freely about a vertical axis through its centre with constant angular velocity ω. A boy of mass 30kg starts from the centre and moves along a radius to the edge of the disk. The angular velocity of the disk now is
View SolutionA uniform horizontal circular platform of mass 200kg is rotating at 5 rpm about vertical axis passing through its centre. A boy of mass 80kg is standing at its edge. if boy moves to centre of platform, find out final angular speed
View SolutionA horizontal disc rotates freely with angular velocity ω about a vertical axes through its centre. A ring having the same mass and radius as the disc, is now gently placed coaxially on the disc. After some time, the two rotate with a common angular velocity. then.
View SolutionA smoothh disc is rotating with uniform angular speed ω about a fixed vertical axis passing through its centre and normal to its plane as shown. A small block of mass m is gently placed at the periphery of the disc. Then (pickup the correct alternative or alternatives)

View SolutionA uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
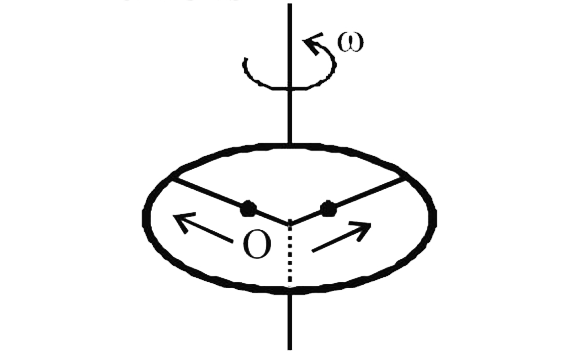
View SolutionA ring of mass M and radius R is rotating with angular speed ω about a fixed vertical axis passing through its centre O with two point masses each of mass M8 at rest at O. These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed of the system is 89ω and one fo the masses is at a distance of 35R from O. At this instant the distance of the other mass from O is
View SolutionA uniform disc of radius a and mass m, is rotating freely with angular speed ω in a horizontal plane about a smooth fixed vertical axis through its centre. A particle, also of mass m, is suddenly attached to the rim of the disc of the disc and rotates with it. The new angular speed is
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω. another disc of the same dimensions but of mass M/4 is placed gently on the first disc coaxially. The angular velocity of the system now is 2ω/√5.
View Solution
