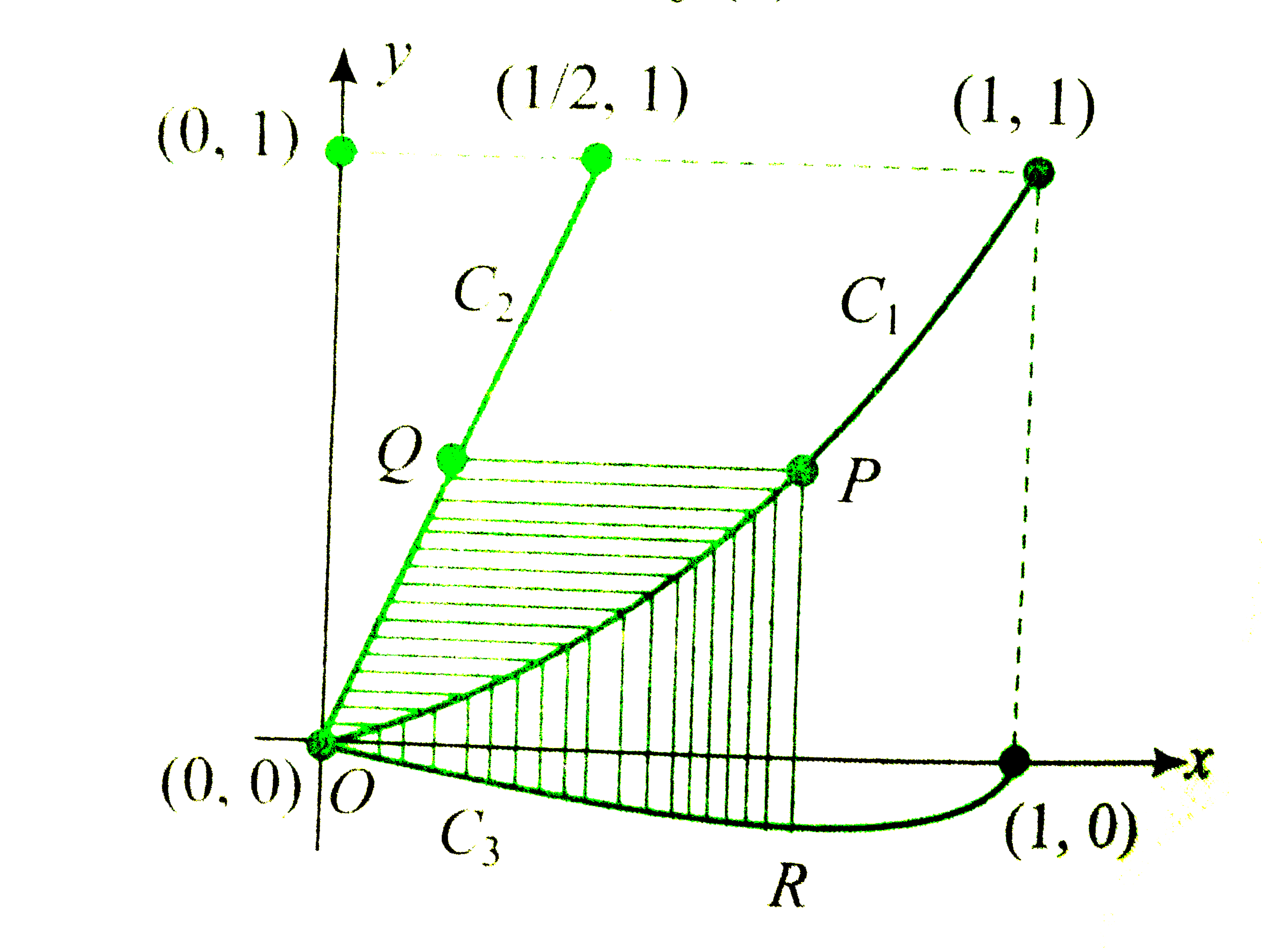
Let C1C2 be the graphs of the functions y=x2 and y=2x, respectively, where 0≤x≤1. Let C3 be the graph of a function y=f(x), where 0≤x≤1,f(0)=0. For a point P on C1, let the lines through P, parallel to the axis, meet C2 and C3 at Q and R, respectively (see Figure). If for every position of P(onC1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x)Solution in Bengali
Let P be on C1,y=x2be(t,t2)
∴ y co-ordinate of Q is also t2
Now, Q on y =2x where y=t2
∴ x=t2/2
∴ Q(t22,t2)
For point R, x=t and it is on y=f(x)
∴ R(t,f(t))
Given that,
Area OPQ = Area OPR
⇒ ∫t20(√y−y2)dy=∫t0(x2−f(x))dx
Differentiating both sides w.r.t. t, we get
(√t2−t22)(2t)=t2−f(t)
⇒ f(t)=t3−t2
⇒ f(x)=x3−x2
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Solved Examples10videos
AREA
- BOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Concept Application Exercise 9.19videos
AREA
- BOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
Similar Questions
Find the area bounded by the curve x2=y,x2=−yandy2=4x−3
10:00View SolutionFind the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
06:20View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
04:10View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' isView SolutionLet f(x)=M a xi mu m{x2,(1−x)2,2x(1−x)}, where 0≤x≤1. Determine the area of the region bounded by the curves y=f(x),x-axis ,x=0,andx=1.
02:47View SolutionLet C_1 and C_2, be the graph of the functions y= x^2 and y= 2x, 0<=x<= 1 respectively. Let C_3, be the graph of a function y- (fx), 0<=x<=1, f(0)=0. For a point Pand C_2, let the lines through P, parallel to the axes, meet C_2 and C_3, at Q and R respectively. If for every position of P (on C_1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).
View SolutionThe points of discontinuity of the function f(x)={2√x , 0≤x≤1, 4−2x , 1<x
03:41View SolutionLet C1andC2 be the graphs of the functions y=x2andy=2x, respectively, where 0≤x≤1. Let C3 be the graph of a function y=f(x), where 0≤x≤1,f(0)=0. For a point P on C1, let the lines through P, parallel to the axes, meet C2andC3 at Q and R, respectively (see figure). If for every position of P(onC1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).
 03:29View Solution
03:29View SolutionLet f be a function such that f(x+f(y))=f(f(x))+f(y) ∀x,y∈R and f(h)=h for 0ε
where ε>0, then determine f'(x) and f(x).05:45View Solutionमाना C1 और C2 क्रमशः फलन y=x2 औरy=2x,0≤x≤1 के ग्राफ हैं। माना C3 फलन, y=f(x),0≤x≤1,f(0)=0 का ग्राफ है। C1 के एक बिंदु P के लिए माना कि बिन्दु P से होकर जाने वाली तथा अक्षों के समान्तर रेखायें C2 व C3 को क्रमशः Q और R पर मिलती है।
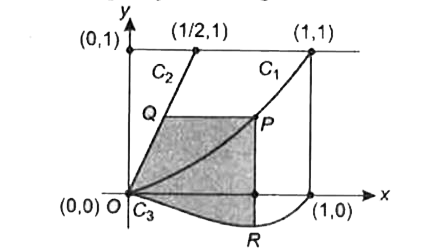 यदिP की प्रत्येक स्थिति ( C1 पर ) के लिए छायांकित क्षेत्र OPQ और ORP का क्षेत्रफल समान हो,तो फलन f(x) को ज्ञात कीजिए। 04:31View Solution
यदिP की प्रत्येक स्थिति ( C1 पर ) के लिए छायांकित क्षेत्र OPQ और ORP का क्षेत्रफल समान हो,तो फलन f(x) को ज्ञात कीजिए। 04:31View SolutionLet f:[0,1]→[0,1] be a continuous function. Then prove that f(x)=x for at least one 0≤x≤1.
02:32View SolutionIn the hexaploid wheat, the haploid (n) and basic (x) numbers of chromosomes are
03:51View SolutionLet C1C2 be the graphs of the functions y=x2 and y=2x, respectively, where 0≤x≤1. Let C3 be the graph of a function y=f(x), where 0≤x≤1,f(0)=0. For a point P on C1, let the lines through P, parallel to the axis, meet C2 and C3 at Q and R, respectively (see Figure). If for every position of P(onC1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x)
10:54View SolutionLet C1andC2 be the graphs of the functions y=x2andy=2x, respectively, where 0≤x≤1. Let C3 be the graph of a function y=f(x), where 0≤x≤1,f(0)=0. For a point P on C1, let the lines through P, parallel to the axes, meet C2andC3 at Q and R, respectively (see figure). If for every position of P(onC1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).
 05:38View Solution
05:38View SolutionThe points of discontinuity of the function f(x)={2√x , 0≤x≤1, 4−2x , 1<x
02:21View SolutionLet f:[0,1]→[0,1] be a continuous function. Then prove that f(x)=x for at least one 0≤x≤1.
05:11View Solution

