In the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.
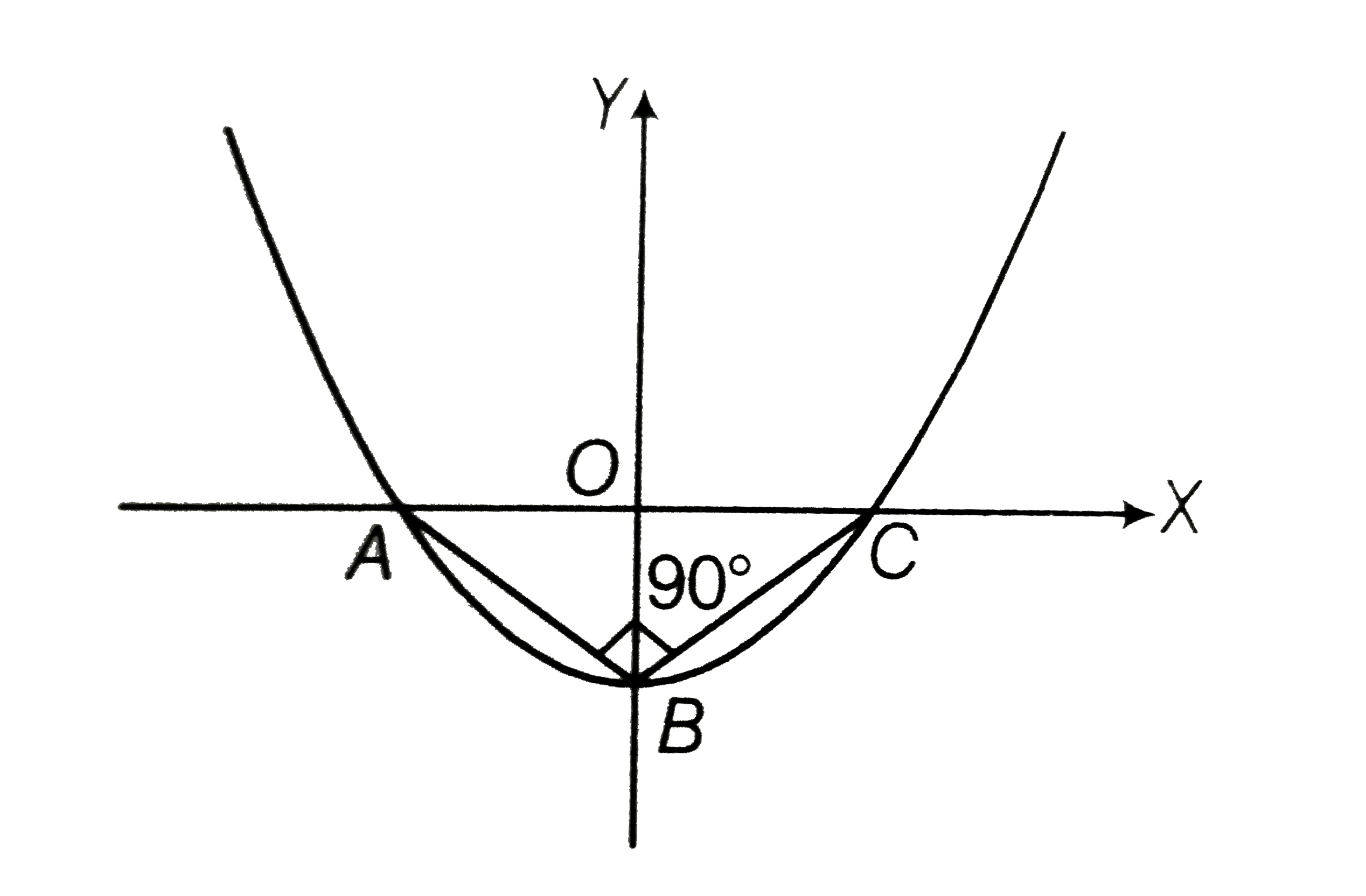
Number of integral value of λ for which λ2 lies between the roots of f(x)=0, is
y=x2−2√2
y=x2−12
y=x22−2
y=x22√2−2√2
The correct Answer is:4
∵AC=4√2
∴AB=BC=4√22=4 units
OB=√42−(2√2)2=2√2
∴A(−2√2,0),C(2√2,0),B(0,−2√2)
Since y=ax2+bx+x passes through A,B and C, we get
y=x22√2−2√2
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - MATRIX MATCH TYPE
6 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - NUMERICAL VALUE TYPE
43 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - Multiple Correct Answer Type
38 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
291 Videos
Similar Questions
In the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.
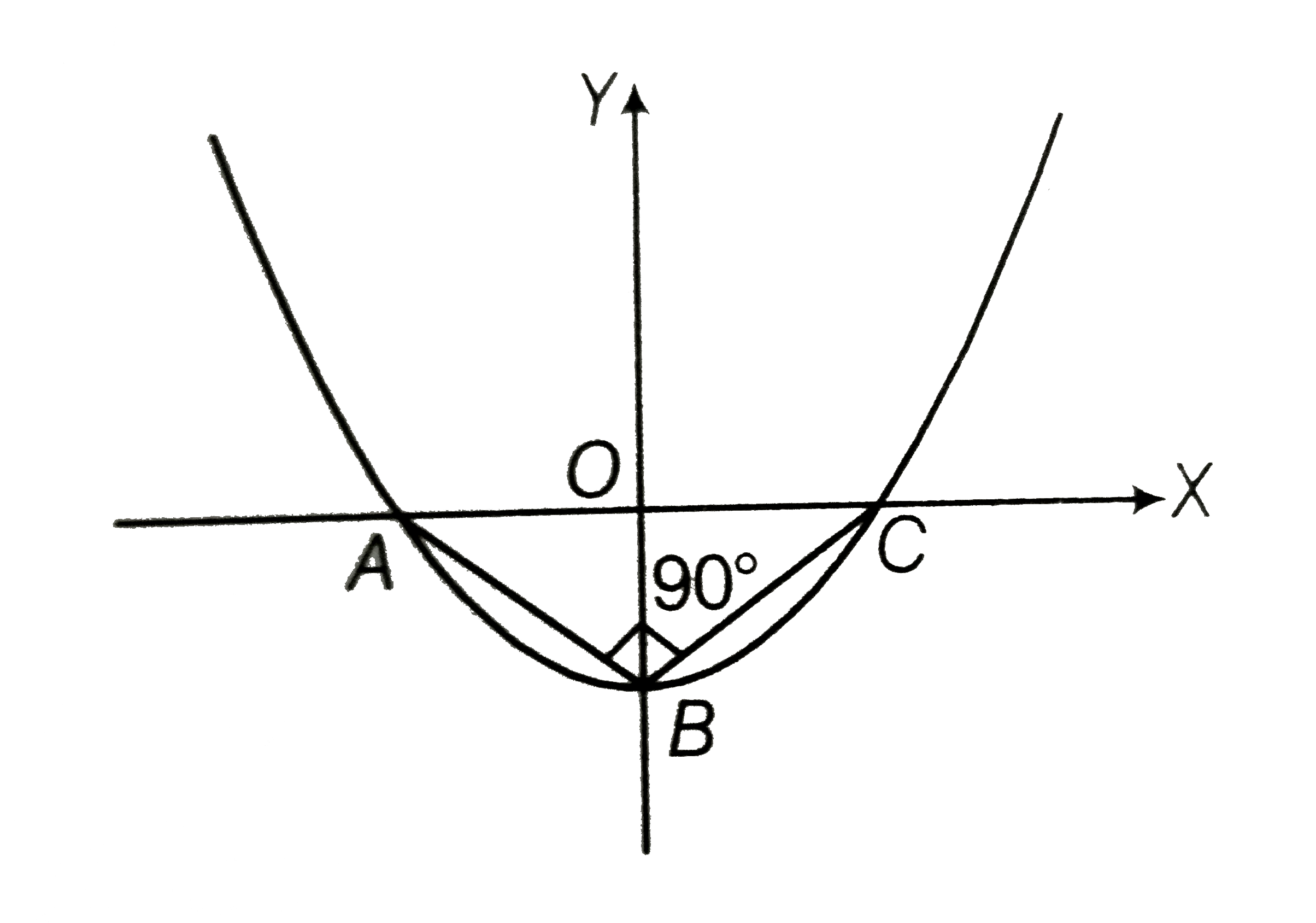
y=f(x) is given by
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔABC is right angled isosceles triangle whose hypotenuse AC=4√2 units.

y=f(x) is given by
View Solution
Knowledge Check
Value of λ so that point (λ,λ2) lies between the lines |x+2y|=3 is
A(−12,2)B(−32,2)C(−32,1)D(−1,32)ΔABC is a right angled isosceles triangle and ∠B is the right angle in the triangle. If AC measures 7√2, then which one of the lengths of AB and BC, respectively?
A7,7B9,9C10,10D11,12
In the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.
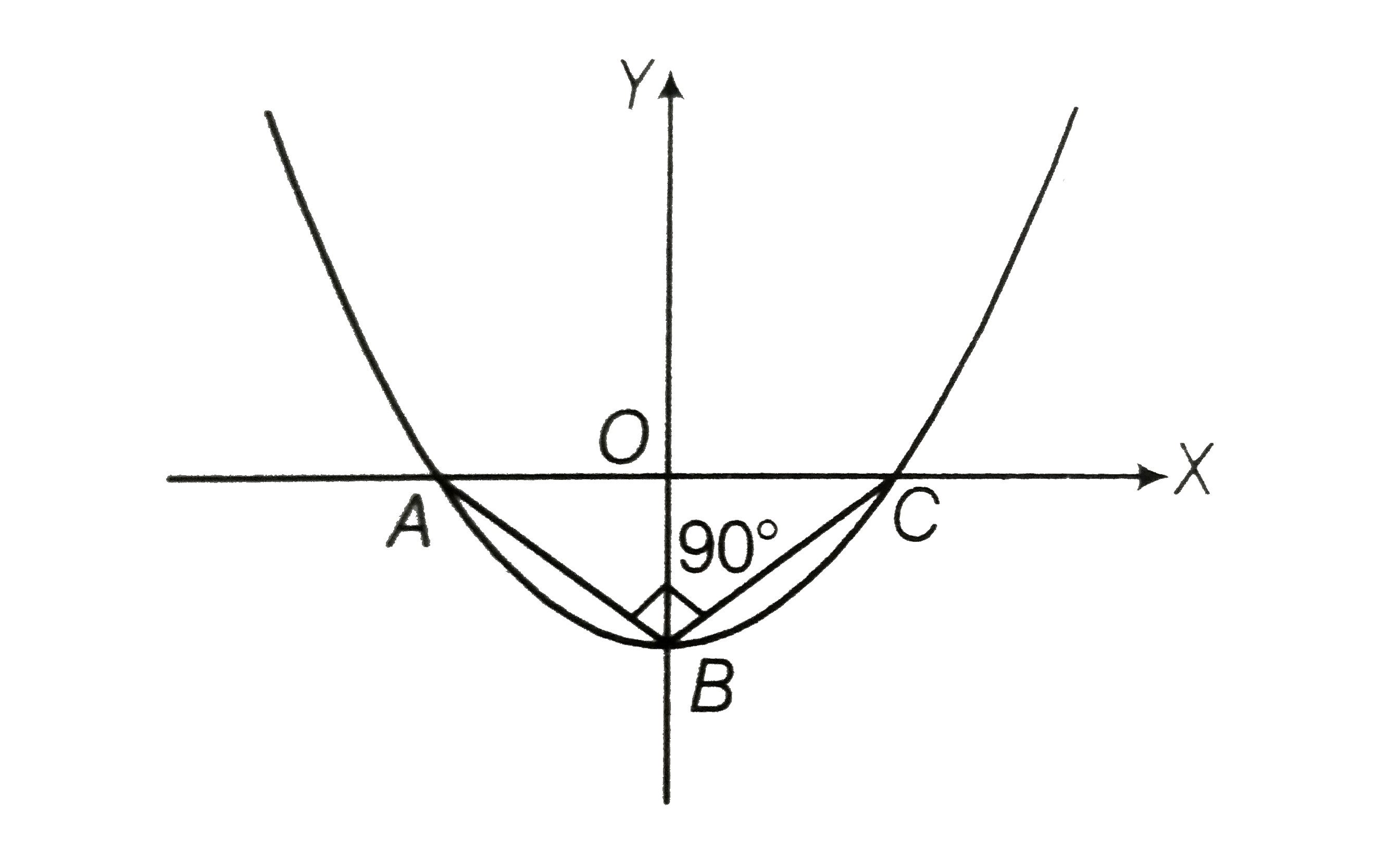
Minimum valueof y=f(x) is
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔABC is right angled isosceles triangle whose hypotenuse AC=4√2 units.

Minimum valueof y=f(x) is
View SolutionIn the given figure, vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔABC is right angled isosceles triangle whose hypotenuse AC=4√2 units. Number of integral values of k for which one root of f(x)=0 is more than k and other less than k
View SolutionValue of λ so that point (λ,λ2) lies between the lines |x+2y|=3 is
View SolutionFind the equations of the sides of an isosceles right angled triangle the equation of whose hypotenuse is 3x+4y=4 and the opposite vertex is the point (2, 2).
View SolutionFind the equations the sides of an isosceles right angled triangle the equation of whose hypotenuse is 3x+4y=4 and the opposite vertex is the point (2, 2).
View Solution
