In the above figure, ACB is a right-angled triangle. CD is the altitude. Circles are inscribed within the ΔACDandΔBCD. P and Q are the centres of the circles. The distance PQ is
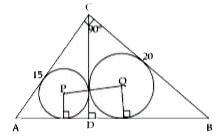
5
√50
7
8
Step by step video & image solution for In the above figure, ACB is a right-angled triangle. CD is the altitude. Circles are inscribed within the DeltaACD and DeltaBCD. P and Q are the centres of the circles. The distance PQ is by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
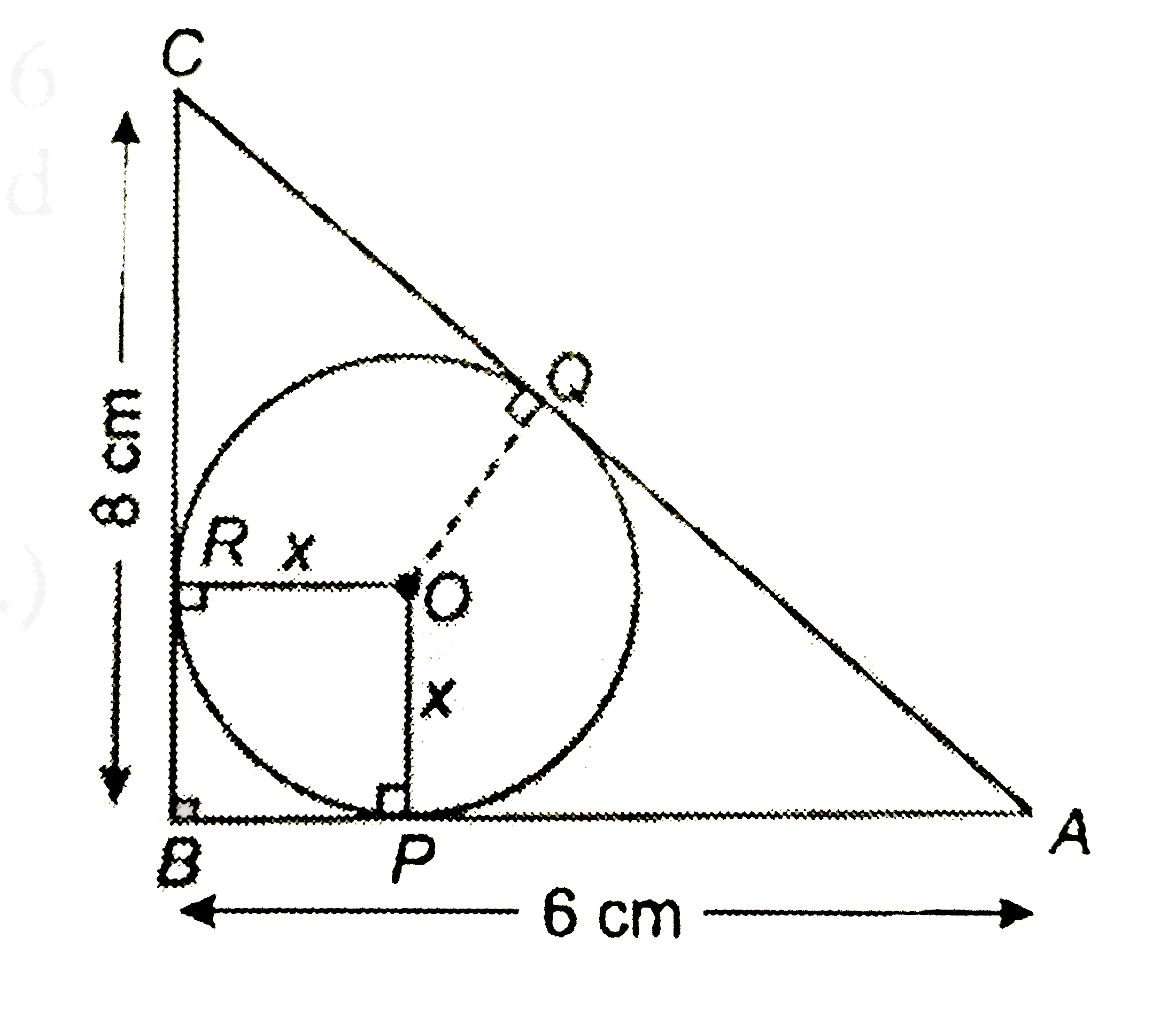
In the given figure ABC is a right angled triangle with AB=6 cm, and BC=8 cm. A circle with centre O has been inscribed inside the triangle. Find the radius of the circle.
View SolutionPQR is a right angled triangle at Q with QR =12 a=cm and PQ=5cm. A circle with centre O is inscribed in △PQR. Find the radius of the circle.
View Solution
Knowledge Check
If a right angled triangle ABC of maximum Δ area is inscribed in a circle of radius R , then
AΔ=2R2Br=(√2−1)RC1r1+1r2+1r3=√2−1RDs=(√2−1)RABC is a right angle triangle right angled at A. A circle is inscribed in it the length of the two sidescontaining right angle are 6 cm and 8 cm then the radius of the circle is
A3 cmB2 cmC5 cmD4 cm
ABC is a right angle triangle right angled at A. A circle is inscribed in it the length of the two sidescontaining right angle are 6 cm and 8 cm then the radius of the circle is
View Solution
In the figure given above AO=CD where
O is the centre of the circle. What is ∠APB equal to ?
View SolutionΔABC is a right angled triangle with ∠A=900AB=bcm,AC=acm,andBC=ccmAcircle is inscribed in this triangle. The radius of the circle,in cm, is:
View SolutionIf I is the incenter of the circle inscribed in the triangle ABC and AI cuts BC at P, then
View SolutionletABC be a right angled triangle at C.If the inscribed circle touches the side ABat D and (AD)(BD)=11, then find the area of triangle ABC..
View SolutionFind the area of right triangle if it is known that the radius of the circle inscribed in the triangle is r and that of the circumscribed circle is R.
View Solution
