A short circuit occurs in a telephone cable having a resistance of 0.45Ωm−1. The circuit is tested with a Wheatstone bridge network have values of 100Ω and 1110Ω respectively. A balance condition is found when the variable resistor has a value of 400Ω. Calculate the distance down the cable, where the short has occured.
The correct Answer is:40 m
To solve the problem of determining the distance down the cable where the short circuit has occurred, we can follow these steps:
Step 1: Understand the Given Information
- Resistance of the cable: Rc=0.45Ω/m
- Resistor values in the Wheatstone bridge: R1=100Ω and R2=1110Ω
- Variable resistor value at balance: Rv=400Ω
Step 2: Define the Resistance of the Cable Segment
Let L be the distance (in meters) from the starting point of the cable to the point where the short circuit occurs. The resistance of this segment of the cable can be expressed as:
RL=Rc×L=0.45×LΩ
Step 3: Apply the Wheatstone Bridge Balance Condition
For a Wheatstone bridge to be balanced, the following condition must hold:
R1RL=R2Rv
Substituting the known values, we have:
1000.45L=1110400
Step 4: Cross-Multiply to Solve for L
Cross-multiplying gives us:
100×400=1110×0.45L
This simplifies to:
40000=499.5L
Step 5: Solve for L
Now, we can solve for L:
L=40000499.5≈80.04m
Step 6: Round the Result
Since we are looking for a practical distance, we can round L to:
L≈80m
Final Answer
The distance down the cable where the short circuit has occurred is approximately 80 meters.
---
- Resistance of the cable: Rc=0.45Ω/m
- Resistor values in the Wheatstone bridge: R1=100Ω and R2=1110Ω
- Variable resistor value at balance: Rv=400Ω
Let L be the distance (in meters) from the starting point of the cable to the point where the short circuit occurs. The resistance of this segment of the cable can be expressed as:
RL=Rc×L=0.45×LΩ
For a Wheatstone bridge to be balanced, the following condition must hold:
R1RL=R2Rv
Substituting the known values, we have:
1000.45L=1110400
Cross-multiplying gives us:
100×400=1110×0.45L
This simplifies to:
40000=499.5L
Now, we can solve for L:
L=40000499.5≈80.04m
Since we are looking for a practical distance, we can round L to:
L≈80m
The distance down the cable where the short circuit has occurred is approximately 80 meters.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(A)16videos
ERROR AND MEASUREMENT
- BOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)22videos
ERROR AND MEASUREMENT
- BOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)22videos
ERROR AND MEASUREMENT
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-289videos
KINEMATICS
Similar Questions
In the simple potentionmeter circuit, where the length AB of the potentiometer wire is 1m, the resistors X and Y have values of 5Ω and 2Ω, respectively. When X is shunted by a wire, the balance point is found to be 0.625m from A. What is the resistance of the shunt?
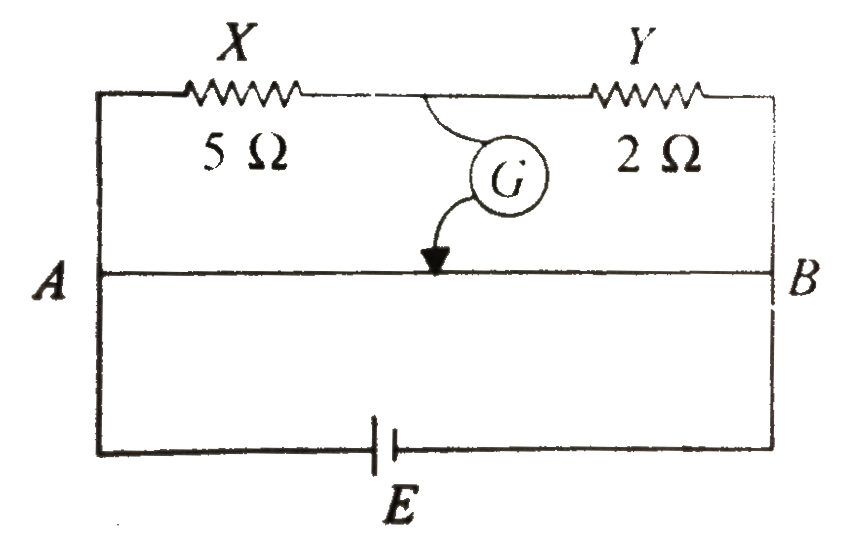 View Solution
View SolutionThe figure below shows a wheatstone bridge with resistors P and Q having almost equal resistance. When R = 400Ω , the bridge is in balanced condition. If on interchanging P and Q, the bridge is again balanced for R=405Ω, then the value of X is
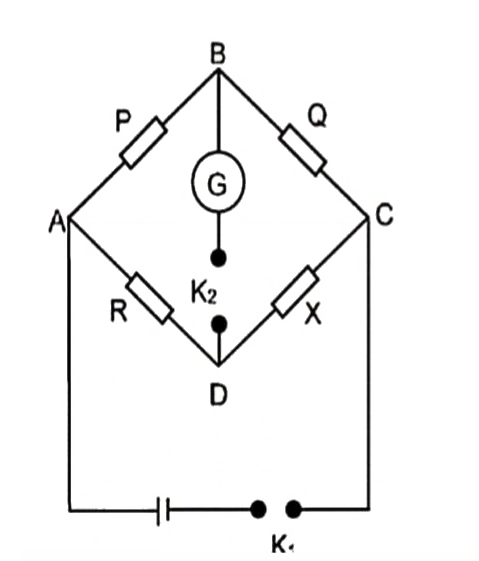 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Four resistances of 3Ω,3Ω,3Ωand4Ω respectively are used to form a Wheatstone bridge. The 4Ω resistance is short circuited with a resistance R in order to get bridge balanced. The value of R will be
A10ΩB11ΩC12ΩD13Ω
Draw the circuit for experimental verification of Ohm's law using a source of variable DC voltage, a main resistance of 100Ω, two galvanometers and two resistances of value 106Ω and 10−3Ω respectively. Clearly show the positions of the voltmeter and the ammeter.
View SolutionDraw the circuit for experimental verfication of Ohm's law using a source of variable DC voltage, a main resistance of 100(Ω), two galvanometers and two resistances of values 106Ω and 10−3 respectively. Clearly show the positions of the voltmeter and the ammeter.
View SolutionA battery of emf E0=12V is connected across a 4m long uniform wire having resistance 4Ωm. The cells of small
emfs ε1=2V and ε2−4V having internal resistance 2Ω and 6Ω respectively, are connected as shown in the figure. If galvanometer shows no deflection at the point N, the distance of point N from teh point A is equal to
 View Solution
View SolutionFour resistors A, and D form a Wheatstone bridge.
The bridge is balanced , when C = 100Ω If A and B are interchanged the bridge balances for C=121Ω. The value of D isView SolutionThe resistance in two arms of the meter bridge is 10Ω and x respectively. The balance length is l1from left. Now the resistance of 10Ω is shunted with another resistor of resistance equal to unknown resistance x then new balance point is 0.75l1 The value of resistance x is
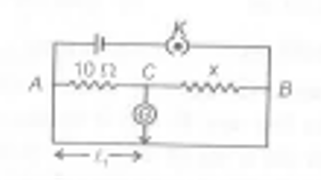 View Solution
View SolutionA cell can be balanced against 110cm and 100cm of potentiometer wire, respectively with and without being short circuited through a resistance of 10Ω. Its internal resistance is
View SolutionA cell can be balanced against 110cm and 100cm of potentiometer wire, respectively with and without being short circuited through a resistance of 10Ω. Its internal resistance is
View Solution

