Two masses A & B each of 5kg are suspended by a light inextensible string passing over a smooth massless pulley such that mass A rest on smooth table & B is held at the position shown. Mass B is now gently lifted up to the pulley and allowed to fall from rest. Determine up to what height will A rise for the ensuing motion.
The correct Answer is:1.25m
To solve the problem step by step, we will analyze the motion of the two masses A and B.
Step 1: Understand the System
We have two masses, A and B, each of mass 5 kg. Mass A is resting on a smooth table, and mass B is held at a height and then allowed to fall. When mass B falls, it will cause mass A to rise due to the tension in the string.
Step 2: Analyze the Motion of Mass B
When mass B is released from rest, it will fall under the influence of gravity. The height from which mass B falls is the same height that mass A will rise. We can denote the height that mass B falls (and thus the height that mass A rises) as h.
Step 3: Apply Energy Conservation
Since there are no non-conservative forces doing work (the pulley is massless and frictionless), we can use the principle of conservation of energy. The potential energy lost by mass B will be equal to the potential energy gained by mass A.
The potential energy lost by mass B when it falls a height h is:
PEB=mB⋅g⋅h=5⋅g⋅h
The potential energy gained by mass A when it rises a height h is:
PEA=mA⋅g⋅h=5⋅g⋅h
Step 4: Set the Energies Equal
Since the potential energy lost by mass B is equal to the potential energy gained by mass A, we can set these two equations equal to each other:
5⋅g⋅h=5⋅g⋅h
This is trivially true, indicating that the system conserves energy.
Step 5: Determine the Height
To find the height h that mass A rises, we need to consider the distance that mass B falls. If mass B is lifted to the pulley and then released, it will fall a distance equal to the length of the string that was initially held.
Assuming mass B falls a distance h, mass A will rise the same distance h. Thus, if mass B falls from a height of 1 meter (for example), mass A will rise by the same height.
Conclusion
If mass B is released from a height of 1 meter, mass A will rise to a height of 1 meter as well. Therefore, the height h that mass A rises is:
h=1 meter
We have two masses, A and B, each of mass 5 kg. Mass A is resting on a smooth table, and mass B is held at a height and then allowed to fall. When mass B falls, it will cause mass A to rise due to the tension in the string.
When mass B is released from rest, it will fall under the influence of gravity. The height from which mass B falls is the same height that mass A will rise. We can denote the height that mass B falls (and thus the height that mass A rises) as h.
Since there are no non-conservative forces doing work (the pulley is massless and frictionless), we can use the principle of conservation of energy. The potential energy lost by mass B will be equal to the potential energy gained by mass A.
PEB=mB⋅g⋅h=5⋅g⋅h
PEA=mA⋅g⋅h=5⋅g⋅h
Since the potential energy lost by mass B is equal to the potential energy gained by mass A, we can set these two equations equal to each other:
5⋅g⋅h=5⋅g⋅h
This is trivially true, indicating that the system conserves energy.
To find the height h that mass A rises, we need to consider the distance that mass B falls. If mass B is lifted to the pulley and then released, it will fall a distance equal to the length of the string that was initially held.
If mass B is released from a height of 1 meter, mass A will rise to a height of 1 meter as well. Therefore, the height h that mass A rises is:
h=1 meter
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV B14videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V A20videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III42videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
Similar Questions
Two masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)
 View Solution
View SolutionTwo masses m and M(>m) are joined by a light string passing over a smooth light pulley. The centre of mass of the system moves with an acceleration
 View Solution
View SolutionTwo masses of 10 kg and 20 kg are connected with an inextensible string passing over two smooth pulleys as shown in the figure. The acceleration of 20 kg mass will be :
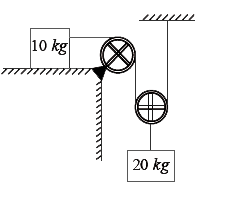 View Solution
View SolutionTwo masses 2 kg and 4 kg are connected at two ends of light inextensible string passing over a frictionless pulley . If the masses are released , then find the accelaration of the masses and the tension in the string .
View SolutionTwo masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View SolutionTwo particles having mass ratio n:1 are interconnected by a light inextensible string that passes over a smooth pulley . If the system is released , then the acceleration of the centre of mass of the system is
View SolutionTwo masses 5 kg and 3 kg are suspended from the ends of an unstretchable light string passing over a frictionless pulley. When the masses are released, the thrust on the pulley is (g = 10ms−2)
View SolutionTwo masses of 3 kg and 4 kg are connected at the two ends of a light inextensible string that passes over a frictionless pulley. Find the acceleration of the masses and the tension in the string, when the masses are released.
View SolutionTwo masses 6 kg and 4 kg are connected by massless flexible and inextensible string passing over massless and frictionless pulley.The acceleration of centre of mass is (g=10ms^2)
View SolutionTwo masses M and M/ 2 are joint together by means of a light inextensible string passes over a frictionless pulley as shown in figure. When bigger mass is released the small one will ascend with an acceleration of
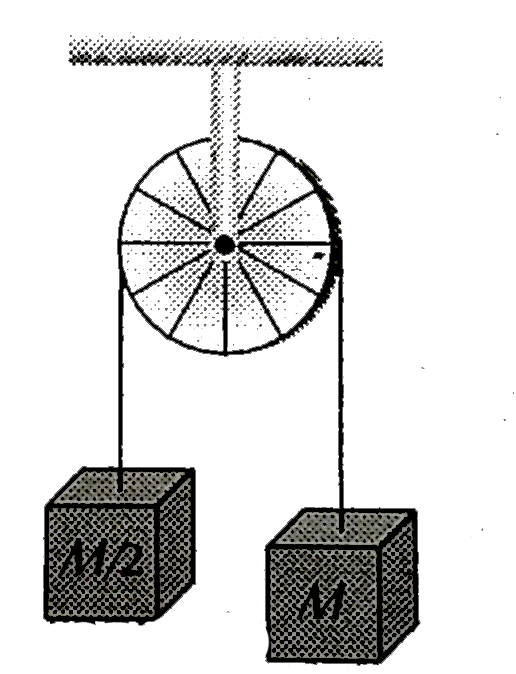 View Solution
View Solution

