Two particles having mass ratio n:1 are interconnected by a light inextensible string that passes over a smooth pulley . If the system is released , then the acceleration of the centre of mass of the system is
(n−1)2 g
(n+1n−1)2g
(n−1n+1)2g
(n+1n−1)g
To find the acceleration of the center of mass of a system consisting of two particles connected by a light inextensible string over a smooth pulley, we can follow these steps:
Step 1: Define the masses
Let the mass of the first particle be m1=nx and the mass of the second particle be m2=x, where n is the mass ratio n:1.
Step 2: Identify the forces acting on the masses
The weight of the first mass (downward) is F1=m1g=nxg and the weight of the second mass (downward) is F2=m2g=xg.
Step 3: Determine the net force and acceleration
Assuming n>1, the first mass will move downward with acceleration a and the second mass will move upward with acceleration a. The net force acting on the system can be expressed as:
Fnet=F1−F2=nxg−xg=(n−1)xg
The total mass of the system is:
mtotal=m1+m2=nx+x=(n+1)x
Using Newton's second law, we can find the acceleration a:
a=Fnetmtotal=(n−1)xg(n+1)x=n−1n+1g
Step 4: Calculate the acceleration of the center of mass
The acceleration of the center of mass acm can be calculated using the formula:
acm=m1a1+m2a2m1+m2
Here, a1=a (downward) and a2=−a (upward), so substituting the values:
acm=(nx)(n−1n+1g)+(x)(−n−1n+1g)nx+x
This simplifies to:
acm=nx⋅n−1n+1g−x⋅n−1n+1g(n+1)x=(n−1)g(n+1)
After canceling x:
acm=(n−1)(n+1)g
Step 5: Final expression for the acceleration of the center of mass
Thus, the acceleration of the center of mass of the system is:
acm=(n−1)(n+1)g
Let the mass of the first particle be m1=nx and the mass of the second particle be m2=x, where n is the mass ratio n:1.
The weight of the first mass (downward) is F1=m1g=nxg and the weight of the second mass (downward) is F2=m2g=xg.
Assuming n>1, the first mass will move downward with acceleration a and the second mass will move upward with acceleration a. The net force acting on the system can be expressed as:
Fnet=F1−F2=nxg−xg=(n−1)xg
The total mass of the system is:
mtotal=m1+m2=nx+x=(n+1)x
Using Newton's second law, we can find the acceleration a:
a=Fnetmtotal=(n−1)xg(n+1)x=n−1n+1g
The acceleration of the center of mass acm can be calculated using the formula:
acm=m1a1+m2a2m1+m2
Here, a1=a (downward) and a2=−a (upward), so substituting the values:
acm=(nx)(n−1n+1g)+(x)(−n−1n+1g)nx+x
This simplifies to:
acm=nx⋅n−1n+1g−x⋅n−1n+1g(n+1)x=(n−1)g(n+1)
After canceling x:
acm=(n−1)(n+1)g
Thus, the acceleration of the center of mass of the system is:
acm=(n−1)(n+1)g
Topper's Solved these Questions
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Only one option is correct for JEE Advanced
Explore 60 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:More a than one option is Correct
Explore 1 Video
- CENTRE OF MASSBook:DC PANDEY ENGLISHChapter:CENTRE OF MASSExercise:Medical entrances gallery
Explore 27 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
Similar Questions
The magnitude of acceleration of centre of mass of the system is

View SolutionTwo particles A and B having equal mass are interconnected by a light inextensible string that passes over a smooth pulley. One of the amsses is pulled downward by a constant force 'F' as shown in diagram, then find the acceleration of the centre of mass of the system (A+B).
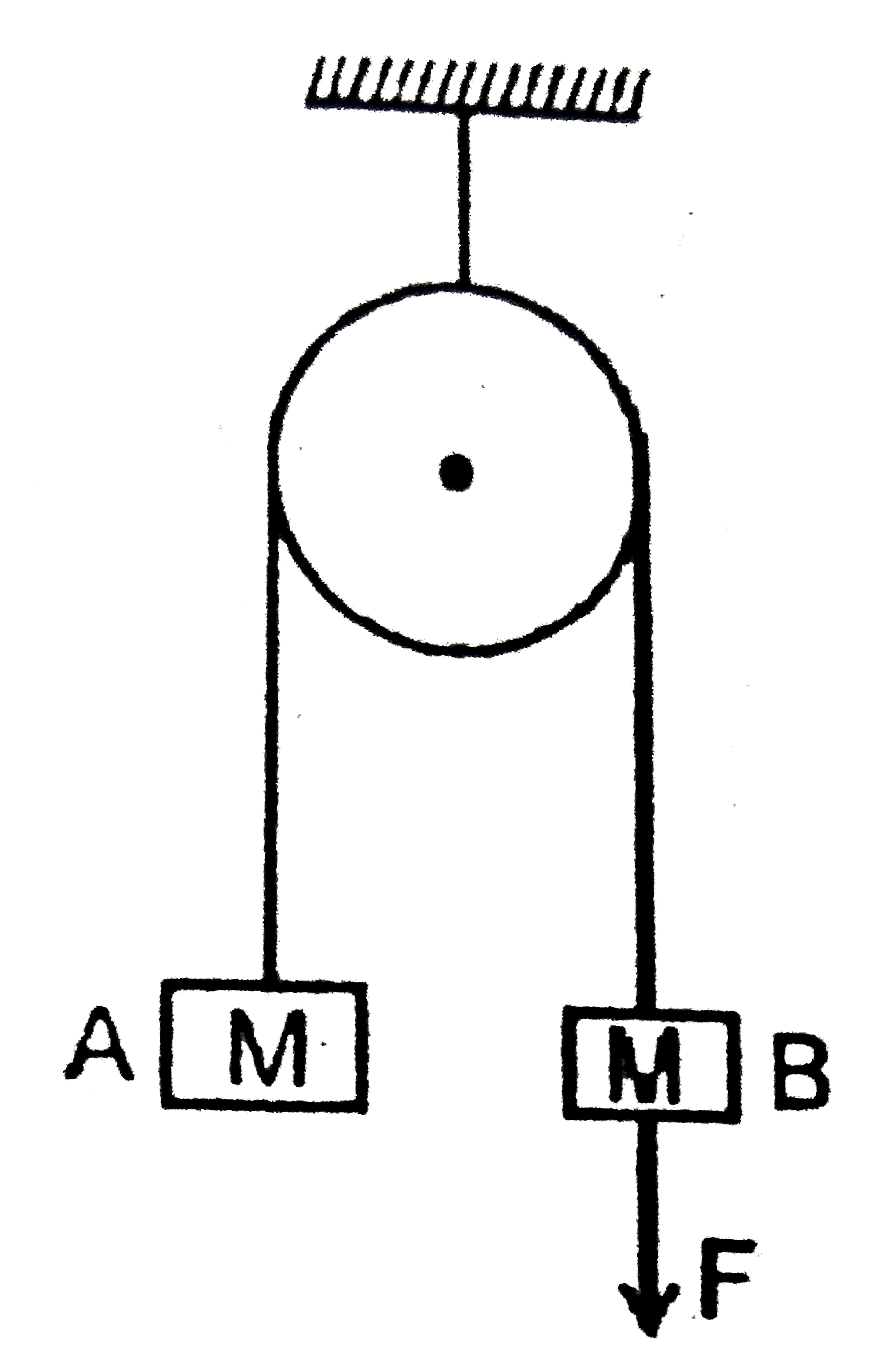
View SolutionTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
View SolutionTwo bodies of masses 1 kg and 2 kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string
View SolutionTwo masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View SolutionTwo masses 2 kg and 4 kg are connected at two ends of light inextensible string passing over a frictionless pulley . If the masses are released , then find the accelaration of the masses and the tension in the string .
View SolutionTwo blocks each of mass 4 kg connected by a light string which is passing over an ideal pulley is as shown in figure. If the system is released from rest then the acceleration (in m/s2) of centre of mass is (g = 10 m/s2)
View SolutionTwo unequal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown . If the system is released from rest, find the work done by string on both the blocks in 1 s.
(Take g=10m/s2).
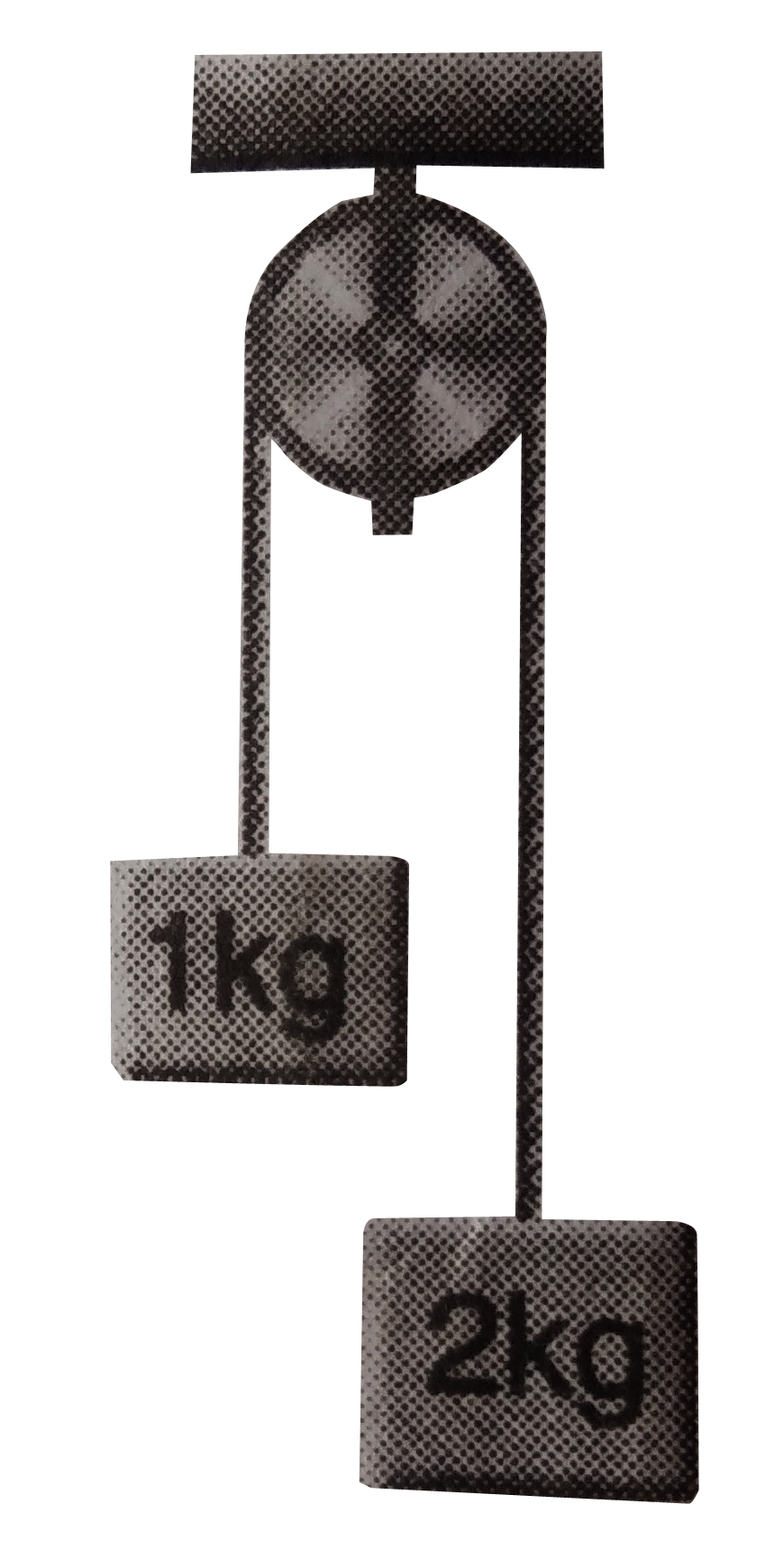
View SolutionA block of mass m1=2 kg is kept on a smooth horizontal table. Another block of mass m2=1 kg is connected to m1 by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
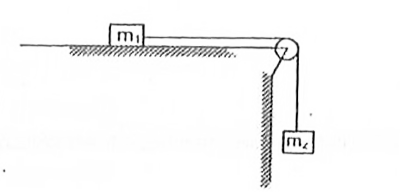
View SolutionTwo particles of masses m and M(M>m) are connected by a cord that passes over a massless, frictionless pulley. The tension T in the string and the acceleration a of the particles is
View Solution