A train moves from one station to another in two hours time. Its speed during the motion is shown in the graph Calculate (i) Maximum acceleration during the journey.
(ii) Distance covered during the time interval from 0.75 hour to 1 hour
The correct Answer is:(i) 160km/hr2 (ii) 10 km
To solve the problem, we will break it down into two parts: calculating the maximum acceleration during the journey and finding the distance covered during the time interval from 0.75 hours to 1 hour.
Part (i): Maximum Acceleration
1. Understanding the VT Graph: The velocity-time (VT) graph shows the speed of the train at different times. The slope of this graph represents acceleration.
2. Identifying Regions: The graph can be divided into three regions based on the changes in speed:
- Region 1: From 0 to 0.5 hours (speed is constant)
- Region 2: From 0.5 to 0.75 hours (speed increases linearly)
- Region 3: From 0.75 to 2 hours (speed decreases linearly)
3. Calculating Acceleration for Each Region:
- Region 1 (0 to 0.5 hours): The speed is constant, so acceleration a1=0.
- Region 2 (0.5 to 0.75 hours): The speed increases from 20 km/h to 60 km/h over 0.25 hours.
- Height = Change in speed = 60−20=40 km/h
- Base = Time interval = 0.75−0.5=0.25 hours
- Acceleration a2=HeightBase=400.25=160 km/h².
- Region 3 (0.75 to 2 hours): The speed decreases from 60 km/h to 20 km/h over 1 hour.
- Height = Change in speed = 60−20=40 km/h
- Base = Time interval = 1 hour
- Acceleration a3=HeightBase=401=40 km/h² (negative since it's deceleration).
4. Finding Maximum Acceleration: The maximum acceleration is the highest value among a1,a2, and a3.
- a1=0 km/h²
- a2=160 km/h²
- a3=40 km/h²
- Therefore, the maximum acceleration is a2=160 km/h².
Part (ii): Distance Covered from 0.75 to 1 Hour
1. Identifying the Area Under the VT Graph: The distance covered during a time interval can be found by calculating the area under the VT graph for that interval.
2. Finding the Area of the Trapezium: The area between 0.75 hours and 1 hour forms a trapezium with:
- One parallel side (speed at 0.75 hours) = 60 km/h
- Other parallel side (speed at 1 hour) = 20 km/h
- Height (time interval) = 1−0.75=0.25 hours
3. Calculating the Area:
- Area of trapezium = 12×(Base1+Base2)×Height
- Area = 12×(60+20)×0.25
- Area = 12×80×0.25=10 km.
4. Final Result: The distance covered during the time interval from 0.75 hours to 1 hour is 10 km.
Summary of Answers:
(i) Maximum acceleration during the journey is 160 km/h².
(ii) Distance covered during the time interval from 0.75 to 1 hour is 10 km.
- Region 1: From 0 to 0.5 hours (speed is constant)
- Region 2: From 0.5 to 0.75 hours (speed increases linearly)
- Region 3: From 0.75 to 2 hours (speed decreases linearly)
- Region 1 (0 to 0.5 hours): The speed is constant, so acceleration a1=0.
- Region 2 (0.5 to 0.75 hours): The speed increases from 20 km/h to 60 km/h over 0.25 hours.
- Height = Change in speed = 60−20=40 km/h
- Base = Time interval = 0.75−0.5=0.25 hours
- Acceleration a2=HeightBase=400.25=160 km/h².
- Region 3 (0.75 to 2 hours): The speed decreases from 60 km/h to 20 km/h over 1 hour.
- Height = Change in speed = 60−20=40 km/h
- Base = Time interval = 1 hour
- Acceleration a3=HeightBase=401=40 km/h² (negative since it's deceleration).
- a1=0 km/h²
- a2=160 km/h²
- a3=40 km/h²
- Therefore, the maximum acceleration is a2=160 km/h².
- One parallel side (speed at 0.75 hours) = 60 km/h
- Other parallel side (speed at 1 hour) = 20 km/h
- Height (time interval) = 1−0.75=0.25 hours
- Area of trapezium = 12×(Base1+Base2)×Height
- Area = 12×(60+20)×0.25
- Area = 12×80×0.25=10 km.
(i) Maximum acceleration during the journey is 160 km/h².
(ii) Distance covered during the time interval from 0.75 to 1 hour is 10 km.
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Exercise-04[B]14videos
KINEMATICS
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Exercise-05 [A]11videos
KINEMATICS
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Comprehension#73videos
KINEMATICS
- BOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)22videos
ERROR AND MEASUREMENT
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
Similar Questions
The velocity-time graph shows the motion of a cyclist. Find (i) its acceleration (ii) its velocity and (iii) the distance covered by the cyclist in 15 seconds.
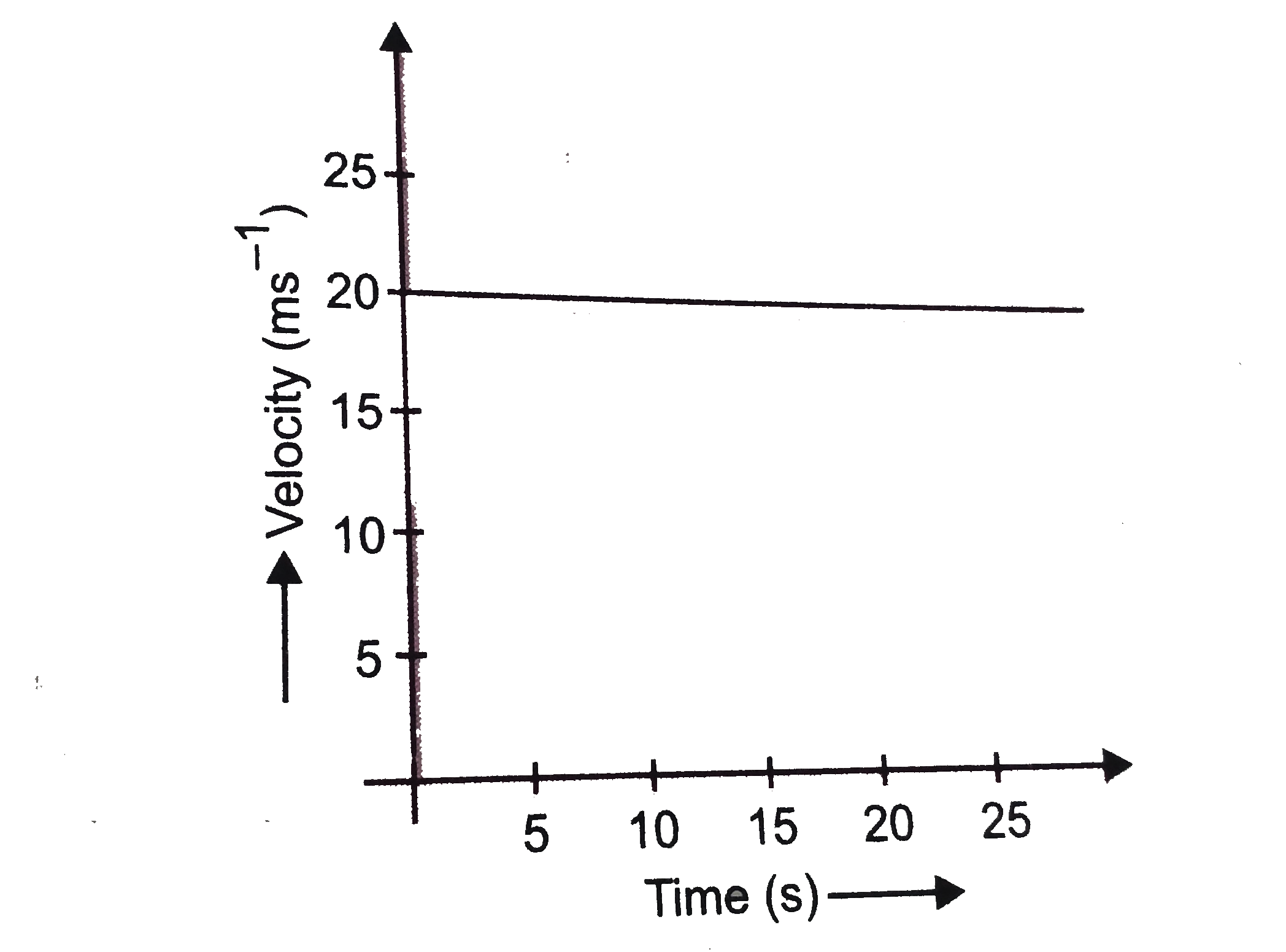 View Solution
View SolutionA car accelerates uniformly from 18km/h to 36km/h in 5 second. Calculate (i) the acceleration and (ii) the distance covered by the car in that time .
View SolutionThe velocity of a particle are given by (4t–2) ms–1 along x–axis. Calculate the average acceleration of particle during the time interval from t = 1 to t = 2s.
View SolutionA train covers 108 km in first two hours ,36 km in next half an hour and 90 km in next two hours .Find the average speed of the train during the whole journey.
View SolutionThe speed verses time graph for a particle is shown in the figure. The distance travelled (in m) by the particle during the time interval t = 0 to t = 5 s will be __________
 View Solution
View SolutionA particle starts from rest at t=0 and undergoes an acceleration as shown in figure.
Draw the velocity-time graph of the motion of the particle during the interval from zero to 4 second.
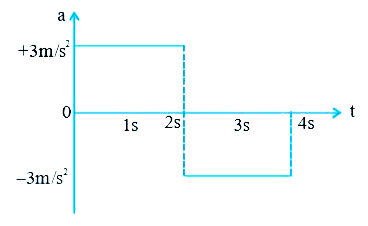 View Solution
View SolutionA subway train travels between two of its stations at then stops with the acceleration shcedule shown in the acceleration versus time graph. Then
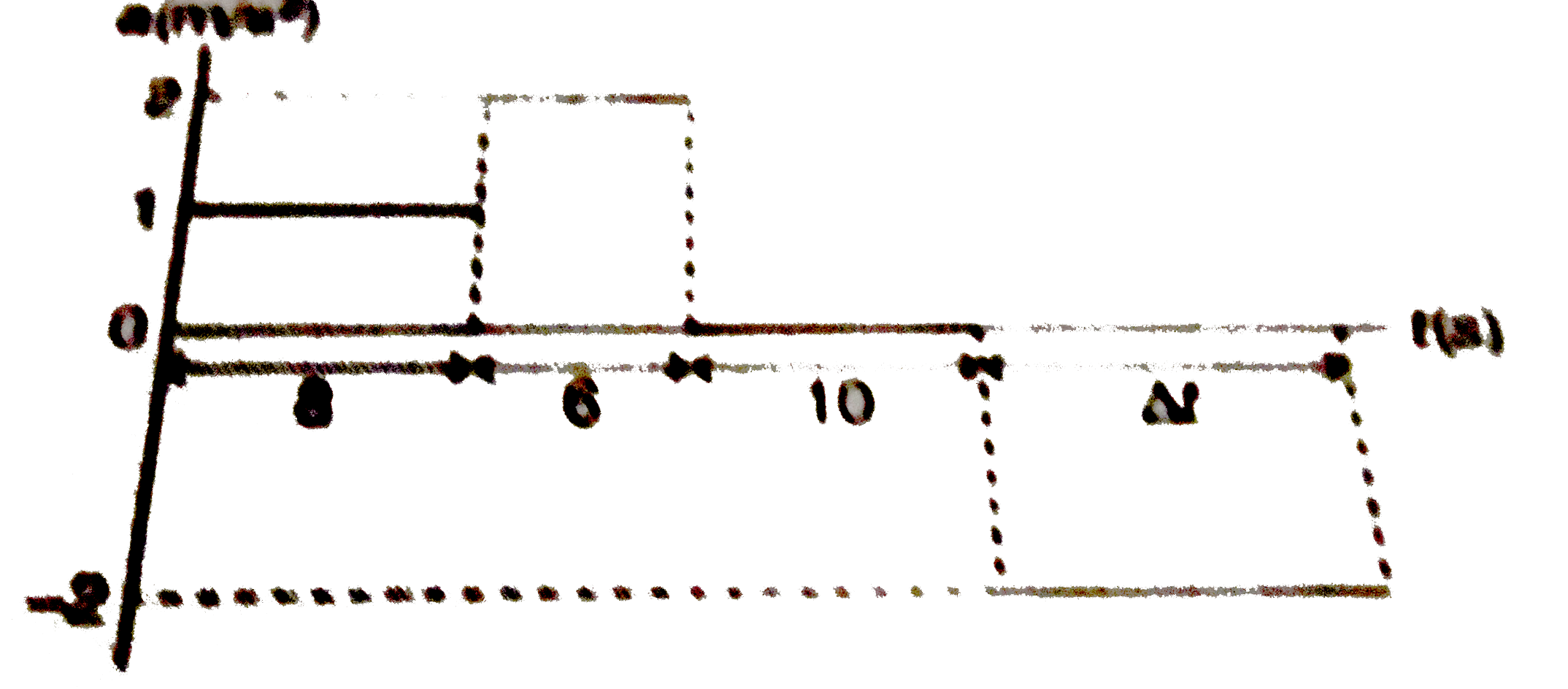 View Solution
View SolutionA body when projected vertically up from ground clovers a total distance D during the time of its flight t. If there were no gravity. The distance covered by it during the same time is equal to
View SolutionA particle moves in a straight line from origin. Its velocity time curve is shown. Find the distance of particle at the =8sec. From the origin and the distance travelled by the particle during first 8 seconds.
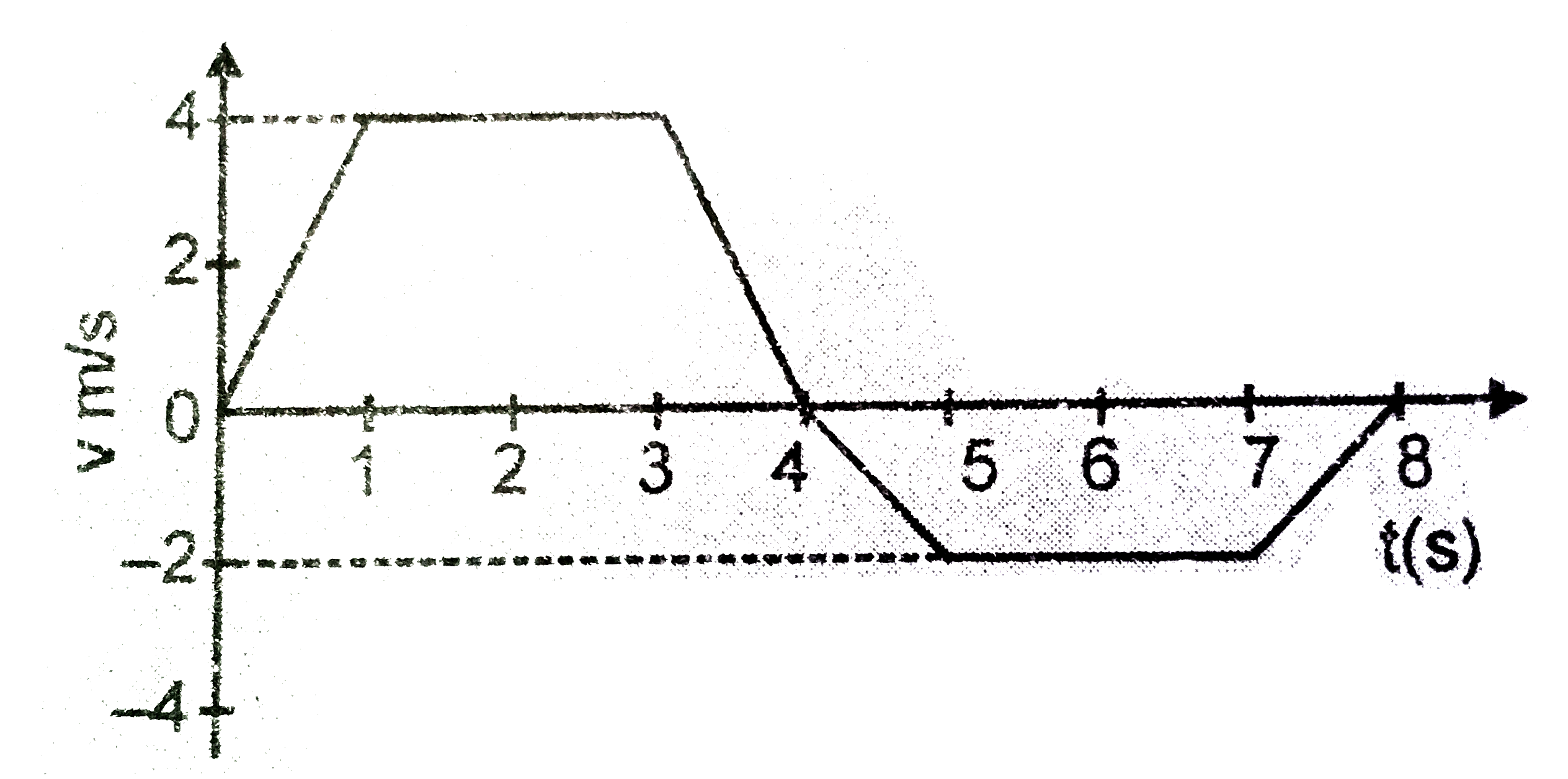 View Solution
View SolutionThe velocity-time graph of a particle in straight line motion is velocity-time graph of a particle in straight line motion is shown in. The particle starts its motion from origin.
 .
.
The distance of the particle from the origin after 8s is .View Solution

