Three ships A, B and C are in motion. The motion of A as seen by B is with speed v towards north-east . The motion. Of B as seen by C is with speed v towards the north-west. Then as seen by A, C will be moving towards
North
South
East
West
The correct Answer is:B
To solve the problem, we need to analyze the relative motions of the ships A, B, and C. We will break down the velocities and their directions step by step.
Step 1: Understanding the Directions
- Ship A is moving towards B with a velocity v towards the North-East.
- Ship B is moving towards C with a velocity v towards the North-West.
Step 2: Representing the Velocity of A with Respect to B
- The North-East direction can be represented as an angle of 45 degrees from both the North and East axes.
- Therefore, the velocity of A with respect to B can be expressed in vector form:
→vAB=vcos(45∘)^i+vsin(45∘)^j=v√2^i+v√2^j
Step 3: Representing the Velocity of B with Respect to C
- The North-West direction can also be represented as an angle of 45 degrees, but this time it is directed towards the West and North.
- Therefore, the velocity of B with respect to C can be expressed as:
→vBC=−vcos(45∘)^i+vsin(45∘)^j=−v√2^i+v√2^j
Step 4: Finding the Velocity of C with Respect to A
- To find the velocity of C with respect to A, we can use the formula:
→vCA=→vCB+→vAB
- Rearranging gives us:
→vCA=→vBC+→vAB
Step 5: Adding the Vectors
- Now substituting the values:
→vCA=(−v√2^i+v√2^j)+(v√2^i+v√2^j)
- Simplifying this:
→vCA=(−v√2+v√2)^i+(v√2+v√2)^j
- The ^i components cancel out:
→vCA=0^i+(2⋅v√2)^j=√2v^j
Step 6: Direction of C with Respect to A
- The positive ^j direction indicates that C is moving towards the North as seen by A.
- However, since we need to find the direction of C as seen by A, we must consider the negative direction:
→vCA=−√2v^j
- This means C is moving towards the South as seen by A.
Final Answer
As seen by A, C will be moving towards the South.
- Ship A is moving towards B with a velocity v towards the North-East.
- Ship B is moving towards C with a velocity v towards the North-West.
- The North-East direction can be represented as an angle of 45 degrees from both the North and East axes.
- Therefore, the velocity of A with respect to B can be expressed in vector form:
→vAB=vcos(45∘)^i+vsin(45∘)^j=v√2^i+v√2^j
- The North-West direction can also be represented as an angle of 45 degrees, but this time it is directed towards the West and North.
- Therefore, the velocity of B with respect to C can be expressed as:
→vBC=−vcos(45∘)^i+vsin(45∘)^j=−v√2^i+v√2^j
- To find the velocity of C with respect to A, we can use the formula:
→vCA=→vCB+→vAB
- Rearranging gives us:
→vCA=→vBC+→vAB
- Now substituting the values:
→vCA=(−v√2^i+v√2^j)+(v√2^i+v√2^j)
- Simplifying this:
→vCA=(−v√2+v√2)^i+(v√2+v√2)^j
- The ^i components cancel out:
→vCA=0^i+(2⋅v√2)^j=√2v^j
- The positive ^j direction indicates that C is moving towards the North as seen by A.
- However, since we need to find the direction of C as seen by A, we must consider the negative direction:
→vCA=−√2v^j
- This means C is moving towards the South as seen by A.
As seen by A, C will be moving towards the South.
Topper's Solved these Questions
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-2)
15 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
Similar Questions
An electron moving towards the east enters a magnetic field directed towards the north. The force on the electron will be directed
View SolutionA horizontal wid is blowing with a velocity v towards north-east. A man starts running towards north with acceleration a. The after which man will feel the wind blowing towards east is
View SolutionA system is shown in the figure. Block A is moving with 1m/s towards left. Wedge is moving with 1m/s towards right. Then speed of the block B will be :
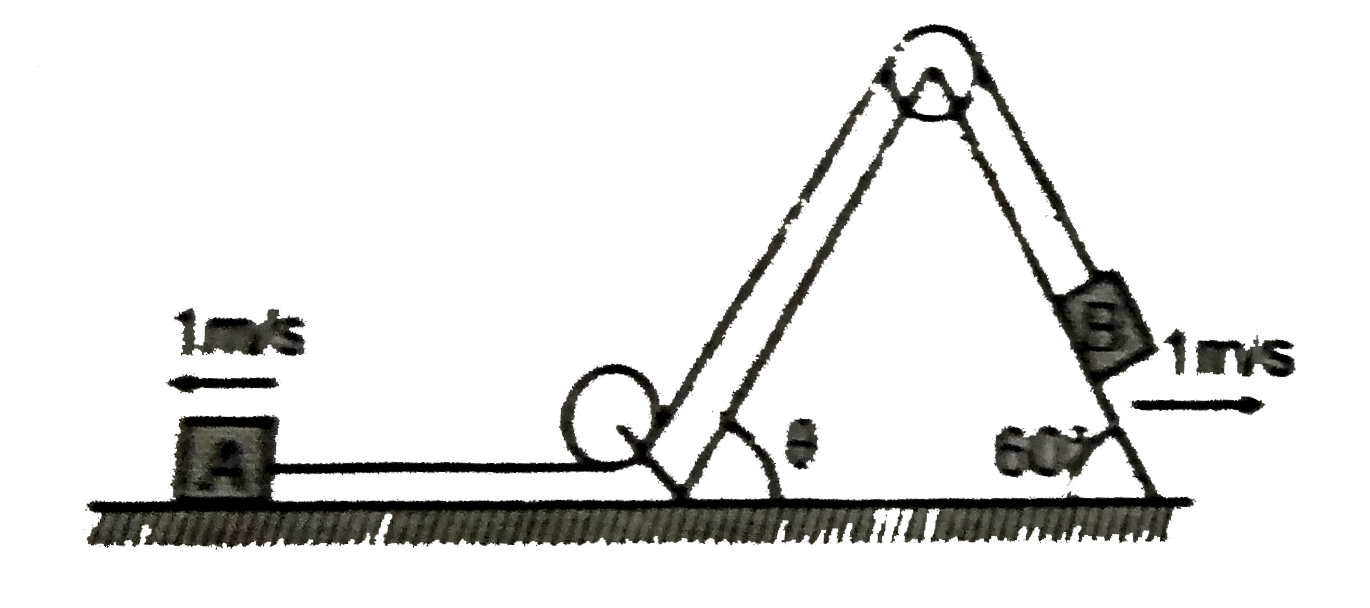
View SolutionA particle of mass m moving in the x direction with speed 2v is hit by another particle of mass 2m moving in the y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to
View SolutionThree masses A, B and C are kept on a smooth horizontal surface as shown in the fiugre. A sharp impulse is given to the mass A, so that it starts moving towards B with speed v0. What is the minimum value of m so that there is only one collision between masses A and B (all collisions are elastic)

View SolutionFrom a light-house an observer two ships A and B. Ship A proceeding towards north at a speed 20√2 km//h and ship B proceeding towards north-east at a speed of 20 km//h. Find in which direction and at what speed the ship B would appear to move to an observer standing on the deck of the ship A.
View SolutionA train is moving due east and a car is moving due north with equal speeds. A passenger in the train finds that the car is moving towards
View SolutionOut of the two cars A and B car A is moving towards east with velocity of 10 m/s whereas B is moving towards north with a velocity 20 m/s, then velocity of A w.r.t B is ( nearly )
View SolutionWhat will be the image speed if
(i) Object is moving towards the plane mirror with speed v ?
(ii) The plane mirror is moving towards the object with speed v ?
View SolutionSTATEMENT -1 : In non - uniform circular motion acceleration of a particles is along the tangent of the circle .
STATEMENT -2 : In uniform circular motion acceleration of a particle is zero .
STATEMENT -3 : In no - uniform circular motion acceleration of a particle is towards the centre of the circle.
View Solution
