Two point masses m1 and m2 at rest in gravity free space are released from distance d. Find the velocity of the CM of the system at the time of collision of particles
Zero
2
3
None
The correct Answer is:A
To solve the problem, we need to find the velocity of the center of mass (CM) of a system consisting of two point masses m1 and m2 when they collide after being released from a distance d in gravity-free space.
1. Understand the Initial Conditions:
- The two point masses m1 and m2 are at rest initially, which means their initial velocities are both zero.
- They are separated by a distance d in a gravity-free space.
2. Identify the Forces Acting on the Masses:
- Since the problem states that it is gravity-free space, there are no external forces acting on the masses.
- Therefore, the net force acting on the system is zero.
3. Apply Newton's Second Law:
- According to Newton's second law, if the net force acting on a system is zero, the acceleration of the system is also zero.
- This implies that the velocities of the masses will not change over time.
4. Calculate the Velocity of the Center of Mass:
- The velocity of the center of mass (CM) of a two-particle system is given by the formula:
vCM=m1v1+m2v2m1+m2
- Since both masses are initially at rest, we have v1=0 and v2=0.
- Substituting these values into the formula gives:
vCM=m1⋅0+m2⋅0m1+m2=0m1+m2=0
5. Conclusion:
- The velocity of the center of mass at the time of collision is 0.
Final Answer:
The velocity of the center of mass of the system at the time of collision of the particles is 0.
---
- The two point masses m1 and m2 are at rest initially, which means their initial velocities are both zero.
- They are separated by a distance d in a gravity-free space.
- Since the problem states that it is gravity-free space, there are no external forces acting on the masses.
- Therefore, the net force acting on the system is zero.
- According to Newton's second law, if the net force acting on a system is zero, the acceleration of the system is also zero.
- This implies that the velocities of the masses will not change over time.
- The velocity of the center of mass (CM) of a two-particle system is given by the formula:
vCM=m1v1+m2v2m1+m2
- Since both masses are initially at rest, we have v1=0 and v2=0.
- Substituting these values into the formula gives:
vCM=m1⋅0+m2⋅0m1+m2=0m1+m2=0
- The velocity of the center of mass at the time of collision is 0.
The velocity of the center of mass of the system at the time of collision of the particles is 0.
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (ROTATIONAL MOTION)
72 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (GRAVITATION)
25 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (CIRCULAR MOTION)
17 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Two point masses m1 and m2 are fixed to a light rod hinged at one end. The masses are at distances l1 and l2 repsectively from the hinge. Find the time period of oscillation (small amplitude) of this system in seconds if m1=m2,l1=1m,l2=3m. If the time period is xπ, then find x.
View SolutionTwo point particles of mass m and 2m are initially separated by a distance 4a. They are then released to become free to move. Find the velocities of both the particles when the distance between them reduces to a.
View SolutionTwo particles of masses m1 and m2 (m1>m2) are separated by a distance d. The shift in the centre of mass when the two particles are interchanged.
View SolutionA rigid uniform rod of mass M and length L is placed along the Y-axis on a smooth horizontal surface with its centre at the origin. Two particles , each of mas m(=M/12) hits simultaneously , at the two ends with equal speed v as shown in the figure. The collision is completely inelastic.
(i) Find the angular velocity of the system after the collision.
(ii) Two particles of mass 2m and m are placed respectively at ( L/2,0) and (−L/2,0). Calculate the time when the rod hits these particles.
View SolutionTwo masses m1 and m2 at an infinite distance from each other are initially at rest, start interacting gravitationally. Find their velocity of approach when they are at a distance r apart.
View SolutionTwo points mass m and 2m are kept at a distance a. Find the speed of particles and their relative velocity of approach when separation becomes a/2.
View SolutionA wedge of mass M is kept at rest on smooth surface a particle of mass m hits the wedge normally. Find the velocity of wedge and particle just after collision. Take coefficient of restitution as e.
View Solution
A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.
View SolutionA circular ring of mass M and radius 'a' is placed in a gravity free space. A small particle of mass m placed on the axis of the ring at a distance √3a from the center of the ring, is released from rest. The velocity with which the particle passes through the center of the ring is
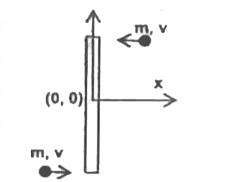
View SolutionTwo balls with masses m1=3 and m2=5kg have initial velocities v1=v2=5m/s in the directions shown in figure. They collide at the origin.
a. find the velocioty of the CM 3s before the collision.
b. Find the position of the CM 2s after the collision.
View Solution
