Particles x (of mass 4 kg) and y (of mass 9 kg) move directly towards each otyher, collide and then separate. If Δvx is the change in the velocity of x and Δvy is the change in velocity of y then the magnitude of ΔvxΔvy is :
94
32
23
49
The correct Answer is:A
To solve the problem, we will use the principle of conservation of momentum. Here are the steps to find the magnitude of the ratio of the changes in velocity of particles x and y after the collision.
1. Define the Variables:
- Let the mass of particle x, mx=4kg
- Let the mass of particle y, my=9kg
- Let the initial velocity of particle x be vx1
- Let the final velocity of particle x be vx2
- Let the initial velocity of particle y be vy1
- Let the final velocity of particle y be vy2
2. Write the Changes in Velocity:
- The change in velocity for particle x is given by:
Δvx=vx2−vx1
- The change in velocity for particle y is given by:
Δvy=vy2−vy1
3. Apply Conservation of Momentum:
- According to the conservation of momentum:
mxvx1+myvy1=mxvx2+myvy2
- Rearranging this gives:
myvy2−vy1=mx(vx2−vx1)
4. Substitute the Changes in Velocity:
- We can express the above equation in terms of changes in velocity:
myΔvy=−mxΔvx
5. Express the Ratio of Changes in Velocity:
- Rearranging the equation gives:
ΔvxΔvy=−mymx
- Substituting the masses:
ΔvxΔvy=−94
6. Find the Magnitude:
- The problem asks for the magnitude of the ratio:
∣∣∣ΔvxΔvy∣∣∣=94
Final Answer:
The magnitude of ΔvxΔvy is 94.
---
- Let the mass of particle x, mx=4kg
- Let the mass of particle y, my=9kg
- Let the initial velocity of particle x be vx1
- Let the final velocity of particle x be vx2
- Let the initial velocity of particle y be vy1
- Let the final velocity of particle y be vy2
- The change in velocity for particle x is given by:
Δvx=vx2−vx1
- The change in velocity for particle y is given by:
Δvy=vy2−vy1
- According to the conservation of momentum:
mxvx1+myvy1=mxvx2+myvy2
- Rearranging this gives:
myvy2−vy1=mx(vx2−vx1)
- We can express the above equation in terms of changes in velocity:
myΔvy=−mxΔvx
- Rearranging the equation gives:
ΔvxΔvy=−mymx
- Substituting the masses:
ΔvxΔvy=−94
- The problem asks for the magnitude of the ratio:
∣∣∣ΔvxΔvy∣∣∣=94
The magnitude of ΔvxΔvy is 94.
Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (ROTATIONAL MOTION)
72 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (GRAVITATION)
25 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (CIRCULAR MOTION)
17 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
Knowledge Check
Three particles of masses 1kg,32kg,and2kg are located the vertices of an equilateral triangle of side a. The x,y coordinates of the centre of mass are.
Aa. 5a9,2a3√3Bb. 2a3√3,5a9Cc. 5a9,2a√3Dd. 2a√3,5a9
A particle of mass 2 kg moves on a circular path with constant speed 10 m/ s . Find change in speed and magnitude of change in velocity. Whan particle completes half revolution.
View SolutionA mass m moving horizontal (along the x-axis) with velocity v collides and sticks to mass of 3m moving vertically upward (along the y-axis) with velocity 2v. The final velocity of the combination is
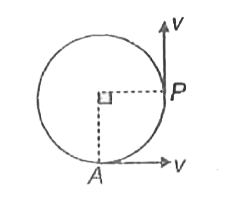
View SolutionA particle of mass 2 kg is moving in circular path with constant speed 20 m/s. The magnitude of change in velocity when particle travels from A to P will be
View SolutionA particle of mass m moving with speed v in position x - direction collides perfectly inelastically with another identical particle moving with same speed in positive y - direction . Find final velocity of the combination.
View SolutionIf y=x4−10 and if x changes from 2 to 1.99, what is the approximate change in y? Also, find the changed value of y.
View SolutionIf y=x4−10 and if x changes from 2 to 1.99, what is the approximate change in y ? Also, find the changed value of y.
View SolutionTwo bodies of different masses 2kg and 4kg are moving with velocities 2m/s and 10m/s towards each other due to mutual gravitational attraction. Then the velocity of the centre of mass is
View Solution
