An unknown resistance r si determined in terms of a standared resistance R=100Ω by using potentiometer. The potential difference across r is balanced againt 45cm length of the wire and that (r+R) is obtained at 70cm of the wire. Find the value of the unknown resistance.
200Ω
280Ω
180Ω
100Ω
The correct Answer is:C
To find the unknown resistance r using the potentiometer, we can use the relationship between the lengths of the wire and the resistances.
1. Identify the Given Values:
- Standard resistance R=100Ω
- Length of wire for r: L1=45cm
- Length of wire for r+R: L2=70cm
2. Use the Potentiometer Formula:
The formula relating the resistances and lengths is given by:
rR=L1L2
Rearranging this gives:
r=R⋅L1L2
3. Substitute the Known Values:
Substitute R=100Ω, L1=45cm, and L2=70cm into the equation:
r=100⋅4570
4. Calculate the Unknown Resistance:
First, calculate 4570:
4570=914≈0.642857
Now multiply by 100:
r=100⋅0.642857≈64.2857Ω
5. Final Calculation:
To get the exact value:
r=100⋅4570=450070=64.2857Ω
Thus, the value of the unknown resistance r is approximately 64.29Ω.
Final Answer:
The unknown resistance r is approximately 64.29Ω.
- Standard resistance R=100Ω
- Length of wire for r: L1=45cm
- Length of wire for r+R: L2=70cm
The formula relating the resistances and lengths is given by:
rR=L1L2
Rearranging this gives:
r=R⋅L1L2
Substitute R=100Ω, L1=45cm, and L2=70cm into the equation:
r=100⋅4570
First, calculate 4570:
4570=914≈0.642857
Now multiply by 100:
r=100⋅0.642857≈64.2857Ω
To get the exact value:
r=100⋅4570=450070=64.2857Ω
The unknown resistance r is approximately 64.29Ω.
Similar Questions
If E is the emf of a cell of internal resistance r and external resistance R, then potential difference across R is given as
View SolutionIn a potentiometer experiment, the balancing length with a resistance of 2Ω is found to be 100cm, while that of an unknown resistance is 500cm. Calculate the value of the unknown resistance.
View Solution
Knowledge Check
A potentiometer wire of length 100 cm has a resistance of 100Ω it is connected in series with a resistance and a battery of emf 2 V and of negligible internal resistance. A source of emf 10 mV is balanced against a length of 40 cm of the potentiometer wire. what is the value of the external resistance?
A790ΩB890ΩC990ΩD1090ΩA cell having an emf E and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
A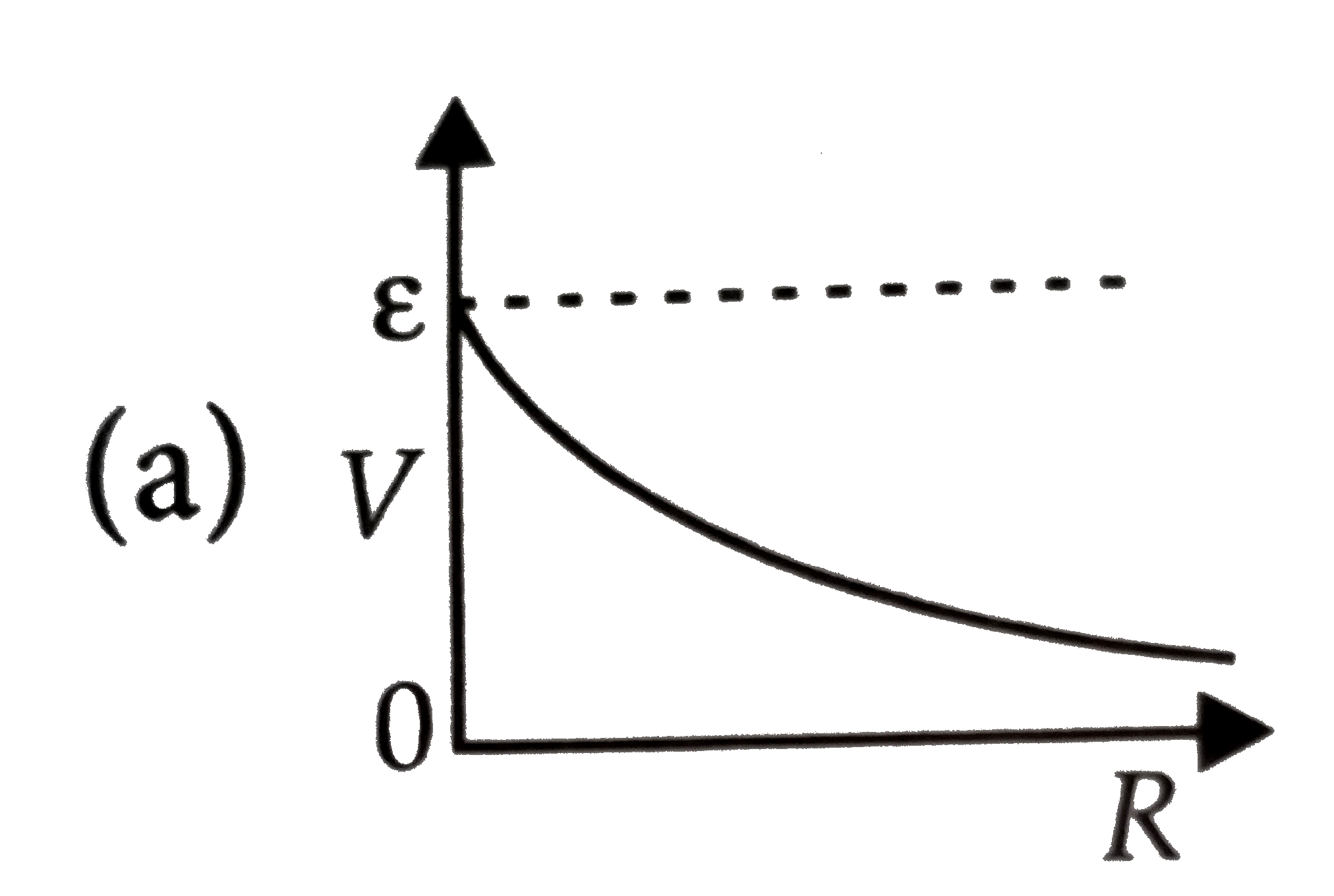 B
B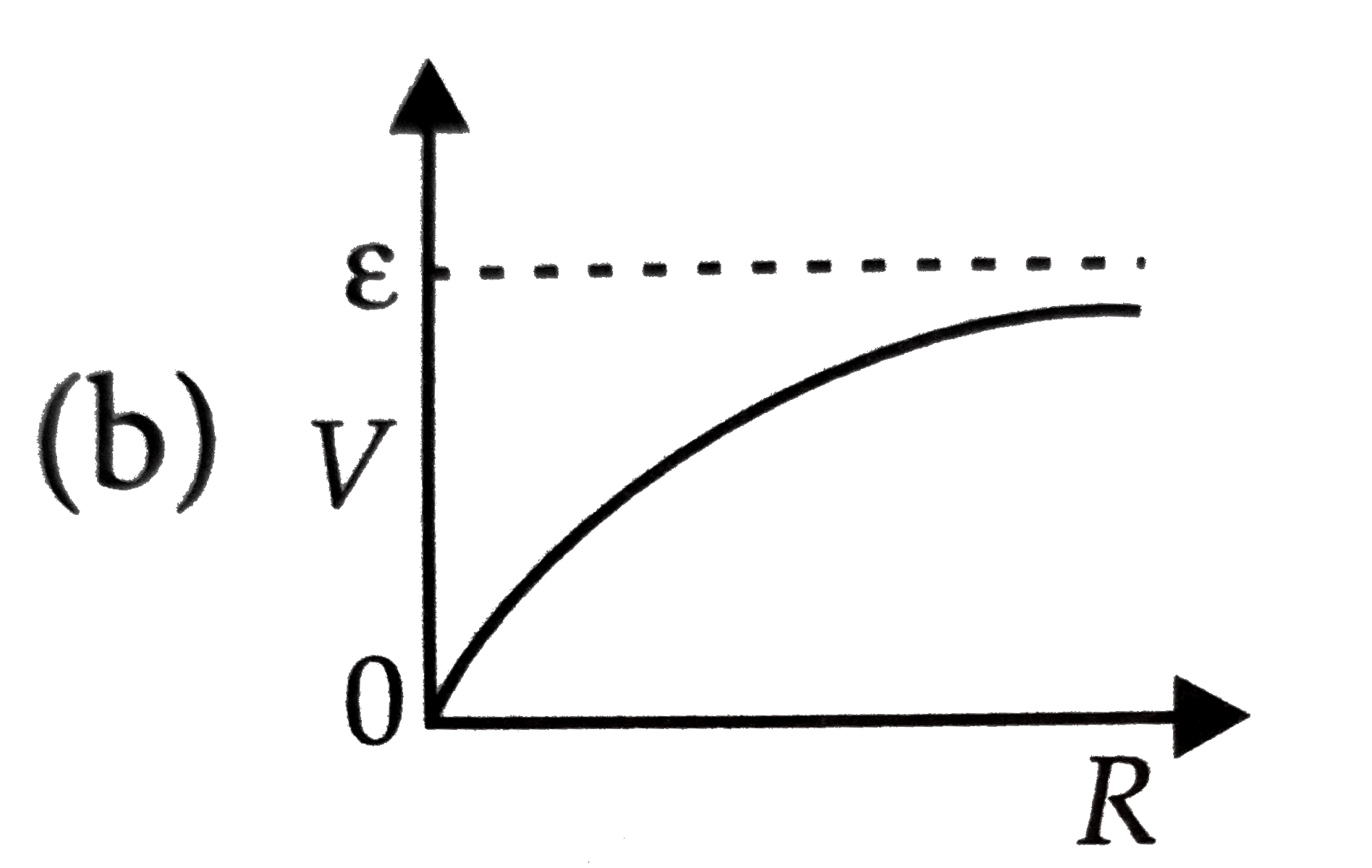 C
C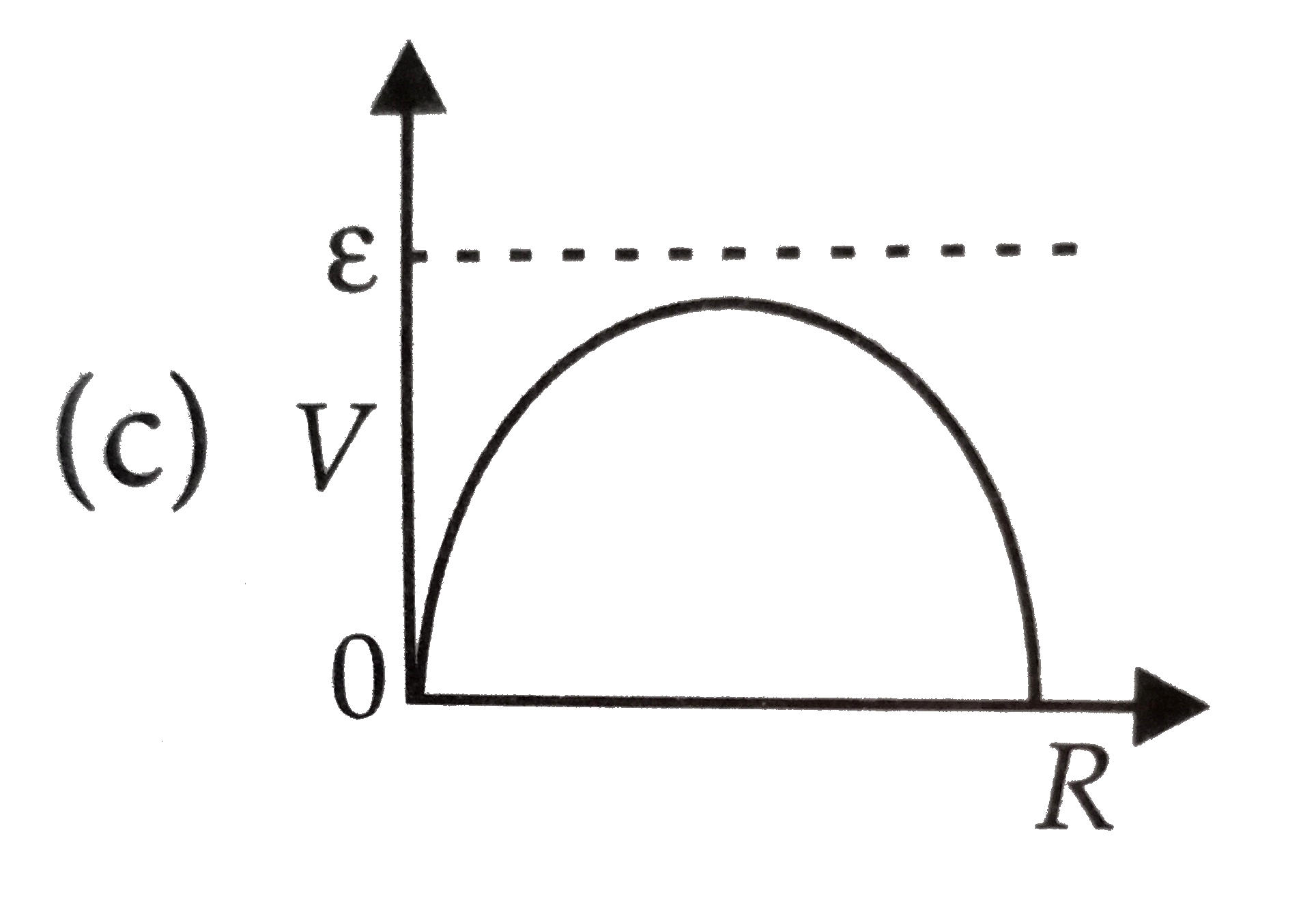 D
D
A potentiometer wire of length 10 m and resistance 10Ω per meter is connected in serice with a resistance box and a 2 volt battery. If a potential difference of 100 mV is balanced across the whole length of potentiometer wire, then then the resistance introduce introduced in the resistance box will be
View SolutionAn unknown resistance R is connected in series with a 2 ohm resistance. A current is flowing in this combination. The balancing length for potential difference across 2 ohm resistor, in a potentiometer experiment is found to be 300 cm, while the balancing length for the potential difference across the unknown R is found to be 360cm. The unknown resistance R is
View Solution
A uniform potentiometer wire AB of length 100 cm has a resistance of 5Ω and it is connected in series with an external resistance R and a cell of emf 6 V and negligible internal resistance. If a source of potential drop 2 V is balanced against a length of 60 cm of the potentiometer wire, the value of resistance R is
View SolutionThe e.m.f. of a standard cell balances across 150 cm length of a wire of potentiometer. When a resistance of 2Ω is connected as a shunt with the cell, the balance point is obtained at 100cm . The internal resistance of the cell is
View SolutionTo the potentiometer wire of L and 10Ω resistance, a battery of emf 2.5 volts and a resistance R are connected in series. If a potential difference of 1 volt is balanced across L/2 length, the value of R is Ω will be
View SolutionFor a wire Rl=12 and length of wire is l=5 cm . If potential differrence of 1V is applied across it current through wire will be : (R = Resistance)
View Solution