A spring is loaded with two blocks m1 and m2 where m1 is rigidly fixed with the spring and m2 is just kept on the block m1. The maximum energy of oscillation is possible for the system having the block m2 in constant with m1 is
m21g22k
m22g22k
(m1+m2)2g22k
None of these
To find the maximum energy of oscillation for the system with blocks m1 and m2, we can follow these steps:
Step 1: Understanding the System
We have a spring with a block m1 rigidly fixed to it, and another block m2 resting on top of m1. The total mass of the system is m1+m2.
Step 2: Formula for Maximum Energy
The maximum energy of oscillation E in a spring-mass system is given by the formula:
E=12kA2
where k is the spring constant and A is the amplitude of oscillation.
Step 3: Finding the Amplitude
The amplitude A can be derived from the relationship between gravitational acceleration g, the angular frequency ω, and the effective mass of the system. The angular frequency ω is given by:
ω=√km1+m2
From this, we can express the amplitude A as:
A=gω2
Substituting ω:
A=gkm1+m2=g(m1+m2)k
Step 4: Substituting Amplitude into Energy Formula
Now, substituting the expression for A back into the energy formula:
E=12k(g(m1+m2)k)2
This simplifies to:
E=12k⋅g2(m1+m2)2k2
E=g2(m1+m2)22k
Step 5: Final Expression
Thus, the maximum energy of oscillation for the system is:
E=g2(m1+m2)22k
Conclusion
The maximum energy of oscillation for the system with blocks m1 and m2 is given by the formula derived above.
---
We have a spring with a block m1 rigidly fixed to it, and another block m2 resting on top of m1. The total mass of the system is m1+m2.
The maximum energy of oscillation E in a spring-mass system is given by the formula:
E=12kA2
where k is the spring constant and A is the amplitude of oscillation.
The amplitude A can be derived from the relationship between gravitational acceleration g, the angular frequency ω, and the effective mass of the system. The angular frequency ω is given by:
ω=√km1+m2
From this, we can express the amplitude A as:
A=gω2
Substituting ω:
A=gkm1+m2=g(m1+m2)k
Now, substituting the expression for A back into the energy formula:
E=12k(g(m1+m2)k)2
This simplifies to:
E=12k⋅g2(m1+m2)2k2
E=g2(m1+m2)22k
Thus, the maximum energy of oscillation for the system is:
E=g2(m1+m2)22k
The maximum energy of oscillation for the system with blocks m1 and m2 is given by the formula derived above.
Topper's Solved these Questions
Similar Questions
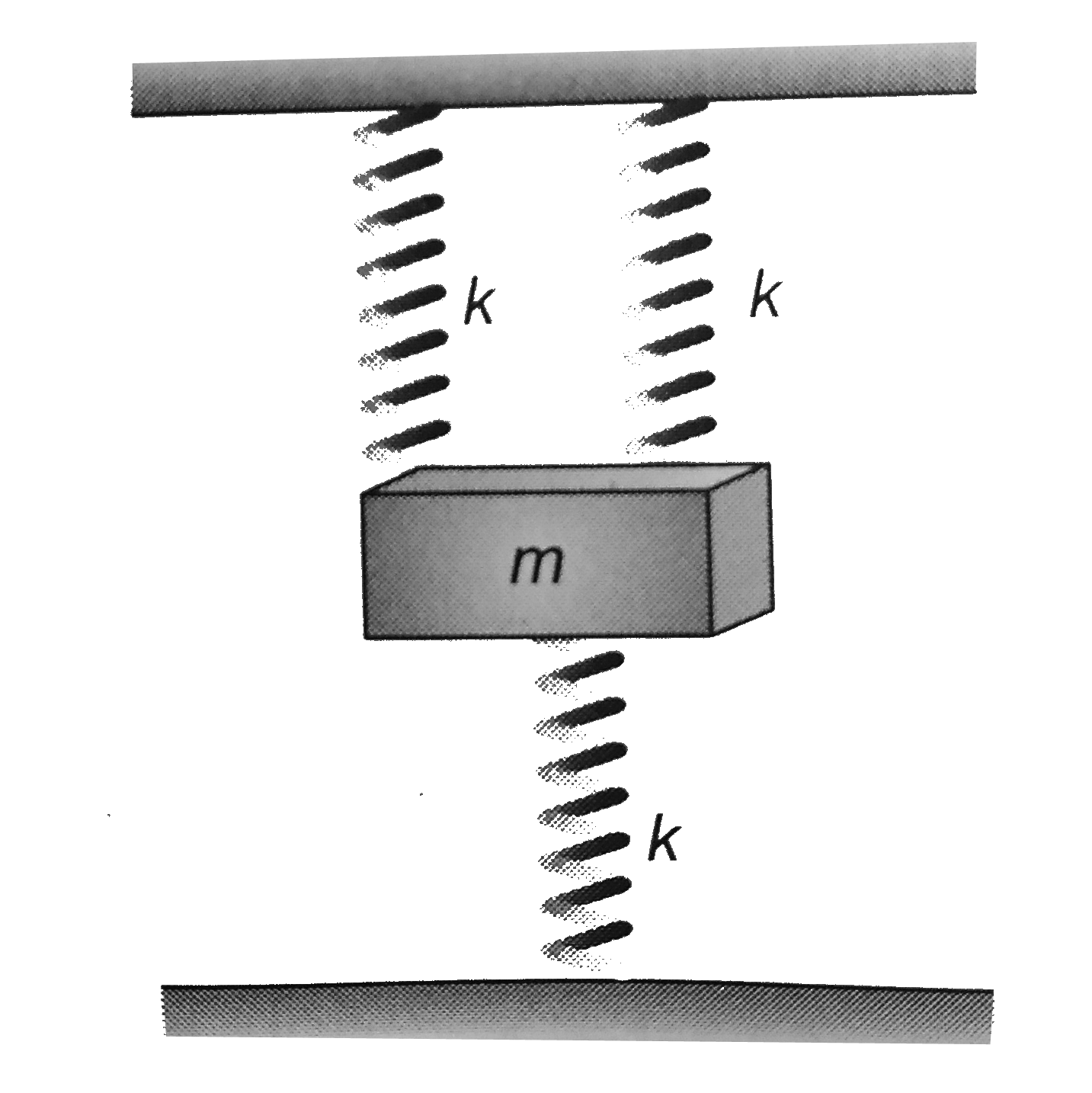
In the figure all spring are identical having spring constant k and mass m each The block also mass m The frequency of oscillation of the block is
 View Solution
View SolutionBlock of mass m2 is in equilibrium as shown in figure. Anotherblock of mass m1 is kept gently on m2. Find the time period of oscillation and amplitude.
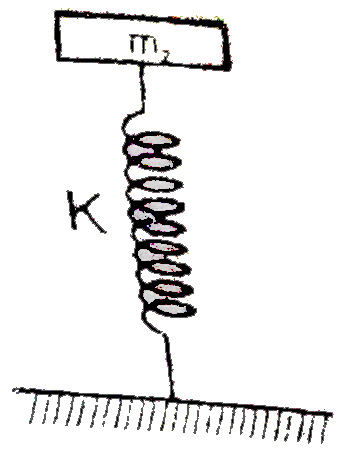 View Solution
View SolutionBlock of mass m2 is in equilibrium as shown in figure. Anotherblock of mass m1 is kept gently on m2. Find the time period of oscillation and amplitude.
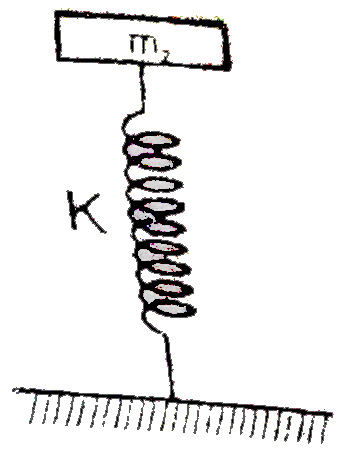 View Solution
View SolutionTwo block of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is:
 View Solution
View Solution
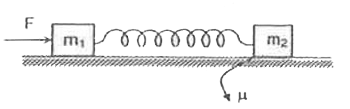
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :View SolutionTwo blocks of masses m1 and m2 are connected by a spring of stiffness k. The coefficient of friction between the blocks and the surface is μ. Find the minimum constant force F to be applied to m1 in order to just slide the mass m2.
 View Solution
View SolutionTwo blocks of masses m1 and m2 are connected to each other with the help of a spring. If pushing force F is given to the mass m1 providing acceleration a to it, then acceleration of m2 is
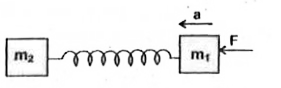 View Solution
View SolutionThe two masses m1 and m2 are joined by a spring as shown. The system is dropped to the ground from a height. The spring will be
 View Solution
View SolutionTwo blocks M1. and M2, are tied with string and kept at rough surface as shown in figure. If F = (2t)N is applied on the block of mass M1, then the friction force on the blocks at t = 2 s. is
 View Solution
View SolutionTwo blocks m1andm2 are in equilibrium. S1 is a string and S2 is a spring of spring constant k. Immediately after the string S1 is cut,
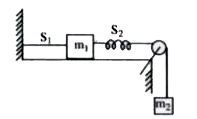 View Solution
View Solution

