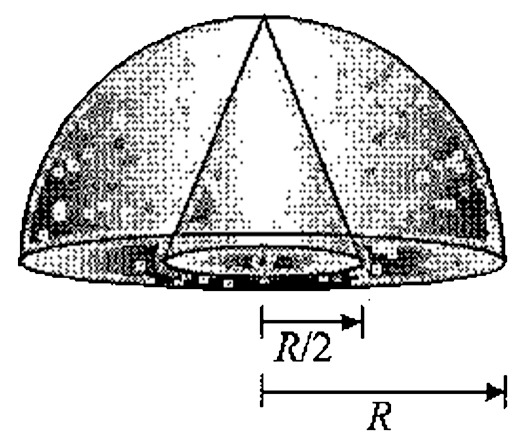
A hemispherical sheli of mass M and radius R made to vibrate as shown in figure. Find its frequency of oscillation.

Centre of mass of the hemispherical shell is at a distance R/2 from the centre of hemisphere.
∴ The torque in displaced position in MgR2sinθ
M.I. of the hemispherical shell about the axis passing through O is 2MR23. (same as the M.I. about a diameter of the base as they are equidistant from the centre of mass)
⇒Iα=−Mg.R2sinθ (Torque and θ oppositely directed)
⇒23MR2α=−MgR2θ(θ is small )
α=34gRθ
ω2=34gR
T=2π√4R3g=4π√R3g

Topper's Solved these Questions
Similar Questions
Knowledge Check
From the given figure find the frequency of oscillation of the mass m
 An=12π√KmBn=12π√K22mCn=2π√m2KDn=12n√K2m
An=12π√KmBn=12π√K22mCn=2π√m2KDn=12n√K2m
Three solid sphere of mass M and radius R are placed in contact as shown in figure. Find the potential energy of the system ?
View SolutionThree solid spheres of mass M and radius R are placed in contact as shown in figure. Find the potential energy of the system ?
View SolutionA rigid rod of mass m with a ball of mass M attached to the free end is restrained to oscillate in a vertical plane as shown in the figure. Find the natural frequency of oscillation.

View SolutionA rigid rod of mass m with a ball of mass M attached to the free end is restrained to oscillate in a vertical plane as shown in the figure. Find the natural frequency of oscillation.

View SolutionFrom a hemisphere of radius R a cone of base radius R/w and height R is cut as shown in figure. Find the height of centre of mass of the remaining object.
View SolutionA ball of radius r is made to oscillate in a bowl of radius R, find its time period of oscillation.
View SolutionA system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?

View Solution
