A block of mass m compresses a spring of stiffness k through a distance 1/2as shown in the figure. If the block is not fixed to the spring, all collisions and elastic and surface is smooth, the period of motion of the block is :
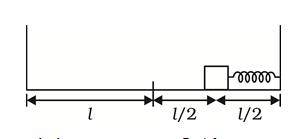
2π√mk
(π+4)√mk
(1+π)√mk
None of these
The period of oscillation =2π√mk
⇒ The period of motion till the block is in contact with the spring is
t=T2=π√mk then it leaves the spring with a speed v=ωA
v=(√km)(l2)
Then it moves with constant velocity v for a distance D=l+l=2l
⇒ The corresponding time of motion =t2=2l/v
⇒t2=2ll2√km=4√mk
∴ The time period of motion =t=t1+t2=π√mk+4√mk
=√mk[π+4].
Topper's Solved these Questions
Similar Questions
A block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is

View SolutionA block of mass m is released from rest onto a spring. A having stiffness kA=mg/2h as shown in figure. If the block compresses spring B through a distance h, find the:

a. stiffness of the spring B
b. equilibrium position of the block
c. maximum velocity of the block
d. maximum acceleration of the block
View SolutionA block of mass m is released from rest onto a spring. A having stiffness kA=mg/2h as shown in figure. If the block compresses spring B through a distance h, find the:

a. stiffness of the spring B
b. equilibrium position of the block
c. maximum velocity of the block
d. maximum acceleration of the block
View SolutionA block of mass m moving at a speed 'v' compresses as spring through a distance 'x' before its speed is halved. Find the spring constant of the spring.
View SolutionA block of mass m is attached to two unstretched springs of spring constants k1andk2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it passes through the mean position shown.

View SolutionA block of mass m is attached to two unstretched springs of springs constant k1 and k2 as shown in figure. The block is displaced towards right through a distance x and is released. Find the speed of the block as it passes through the mean position shown.

View SolutionA block of mass 0.9kg attached to a spring of force constant k is lying on a frictionless floor. The spring is compressed to √2cm and the block is at a distance 1/√2cm from the wall as shown in the figure. When the block is released, it makes elastic collision with the wall and its period of motion is 0.2sec. Find the approximate value of k

View SolutionA block of mass 100g attached to a spring of stiffness 100N/m is lying on a frictionless floor as shown. The block is moved to compress the spring by 10cm and released. If the collision with the wall is elastic then find the time period of oscillations.

View SolutionTwo blocks of masses m and M connected by a light spring of stiffness k, are kept on a smooth horizontal surface as shown in figure. What should be the initial compression of the spring so that the system will be about to break off the surface, after releasing the block m1?
View SolutionA block of mass 1kg is dropped on a spring - mass system as shown in the figure. The block traves 100 meters in the air before strinking the 3 kg mass. Calculate maximum compression in the spring, if both the blocks move together after the collision. Spring constant of the string k=1.25×106.
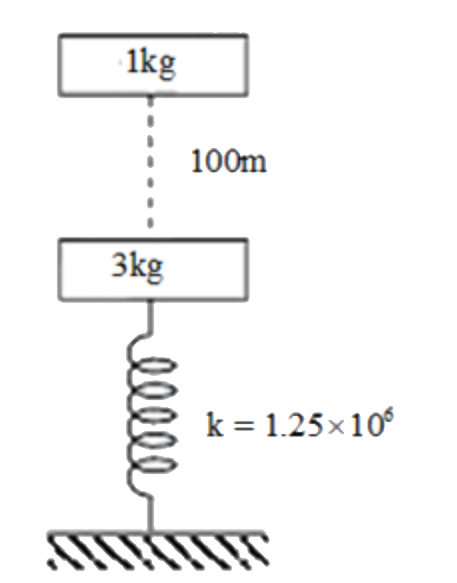
View Solution
